Angeregt durch moderne Zeltdächer oder Flächentragwerke (wie etwa das berühmte Münchner Olympiadach, oder das hier gezeigte Netzdach eines Freigeheges für Affen in der Wilhelma in Stuttgart) stellte sich uns die Frage:
Gibt es eine (differenzierbare) Funktion in zwei Veränderlichen, die zwar mehrere (lokale) Maxima, aber keine lokalen Minima hat?
Beim Zeltdach sind die lokalen Minima lästig und unangenehm – und zwar sowohl bei warmer Luft im Zelt als auch bei Regen von außen: Solch ein lokales Minimum ist ja immer eine Stelle, an der sich Schwitzwasser sammelt und herab tropft, oder gar Regenwasser, das sich außen auf der Plane angesammelt hat, durch diese Plane durch drückt.
Eine mögliche Antwort auf die gestellte Frage stellt der Expowurm dar: Das ist (oder war) ein experimenteller Pavillon der Hochschule Anhalt (FH) – das Bild wurde im August 2014 in Dessau aufgenommen.
Ein einfaches, vom Expowurm inspiriertes Beispiel einer Funktion mit beliebig vielen lokalen Maxima und allerlei Sattelpunkten, aber keinen lokalen Minima erhält man mit \(w\colon\RR^2\to\RR\colon\) \(\binom xy\mapsto \cos(x)-y^2\). In der Tat findet man an jeder Stelle \(\binom x0\) mit \(x\in 2\pi\ZZ\) ein (sogar globales) Maximum, an jeder Stelle \(\binom x0\) mit \(x\in \pi\ZZ\setminus 2\pi\ZZ\) einen Sattelpunkt, und sonst keine kritischen Stellen.
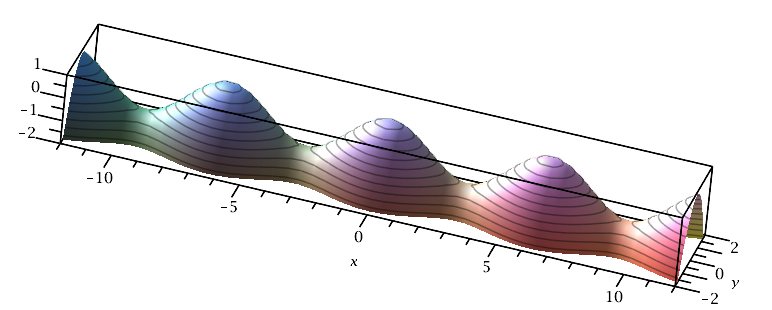
Allerdings waren wir mit solchen Beispielen nicht zufrieden: Hier sitzen die Maxima und die Sattelpunkte hintereinander in einer Reihe, wir hätten gerne eine weniger eindimensionale Konstruktion.
Unsere Wünsche wurden weiter angestachelt durch eine reale Zeltkonstruktion (fotografiert von David Zimmer):


Und in der Tat, wir haben eine einigermaßen einfache Funktion gefunden, die wir im Folgenden vorstellen und eingehend untersuchen wollen:
Wir betrachten die Funktion
\( f\colon \RR^2 \to \RR\colon \) \( \binom xy \mapsto (1-x^2-y^2)x^2y^2-\frac{x^4+y^4}4 \)
in zwei Variablen.
Behauptung: Diese Funktion \(f\) hat vier Maxima, einen Sattelpunkt und keine weiteren kritischen Stellen.
Wir werden im Folgenden zeigen, dass diese Behauptung stimmt – und sogar eine allgemeinere Funktionenschar gründlich analysieren.
Um die lokalen Extrema zu bestimmen, berechnen wir zuerst den Gradienten (also die Liste der partiellen Ableitungen nach den Variablen \(x\) und \(y,\) von denen der Funktionswert abhängt):
Als kritische Stellen suchen wir die Nullstellen des Gradienten. Offensichtlich ist \(P_0 \coloneqq \binom00\) eine solche.
Aus \(\nabla f\binom0y=\binom00\) ergibt sich \(0=-y^3\) und damit \(y=0.\) Ebenso folgt \(x=0\) aus \(\nabla f\binom x0=\binom00.\) Also gilt \(x\ne 0\ne y\) für jede kritische Stelle \(\binom xy\ne\binom00.\) An solchen Stellen reduziert sich die Bedingung \(\nabla f\binom xy = \binom00\) dann zu dem System
\( (\dagger) \qquad \) \( -2x^2y^2+2(1-x^2-y^2)y^2-x^2 = 0 \)
\( (\ddagger) \qquad \) \( -2x^2y^2+2(1-x^2-y^2)x^2-y^2 = 0 . \)
Subtraktion dieser Gleichungen führt auf
\( (*) \qquad \) \( \bigl(2(1-x^2-y^2)+1\bigr)\bigl(x^2-y^2) = 0 . \)
Falls \(x^2 \ne y^2,\) ergibt sich aus Gleichung \((*)\) die Bedingung \(2(1-x^2-y^2)+1 = 0,\) also \(x^2+y^2 = \frac32.\) Eingesetzt in \((\dagger)\) liefert dies dann \(0 = -2x^2y^2+2(1-\frac32)y^2-x^2 \) \( = -2x^2y^2-\frac32. \) Hierfür gibt es keine reelle Lösung \(\binom xy,\) also bleibt nur noch der Fall \(x^2=y^2\) zu betrachten.
Setzt man \(x^2=y^2\) in \((\dagger)\) ein, so ergibt sich \( 0 = -2x^4+2(1-2x^2)x^2-x^2 \) \( = -6x^4+x^2 = x^2(-6x^2+1) .\) Da wir nur noch Fälle mit \(x\ne0\) zu betrachten haben, folgt daraus \(x^2 = \frac1{6},\) und wir haben außer \(P_0=\binom00\) nur noch die vier kritischen Stellen
\( P_1 \coloneqq \frac1{\sqrt6}\binom{1}{1}, \) \( P_2 \coloneqq \frac1{\sqrt6}\binom{1}{-1}, \) \( P_3 \coloneqq \frac1{\sqrt6}\binom{-1}{1}, \) \( P_4 \coloneqq \frac1{\sqrt6}\binom{-1}{-1}. \)
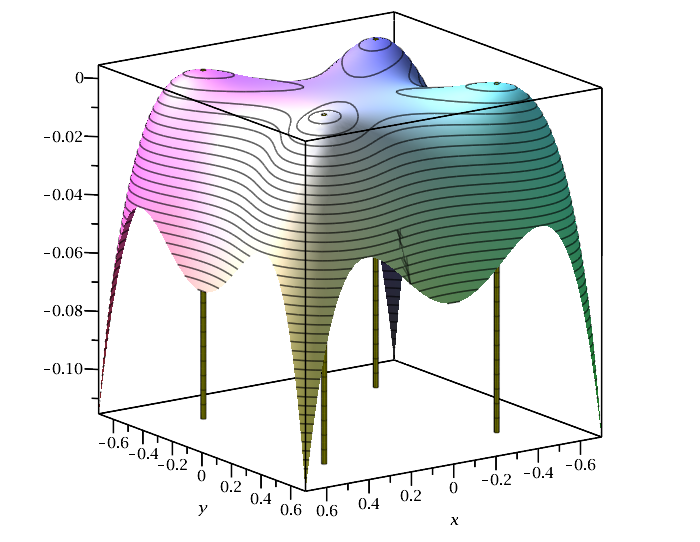
Das Schaubild zeigt einen Ausschnitt aus dem Graphen der Funktion
\(f\) (mit Stützen
bei den kritischen Stellen
\(P_1,P_2,P_3,P_4\)). An diesen vier Stellen suggeriert uns dieses
Schaubild (korrekterweise) das Vorliegen relativer Maxima (das sind
sogar absolute Maxima). Dagegen ist nicht so offensichtlich, was bei
der kritischen Stelle \(P_0\) passiert.
Zur Klärung des Typs einer kritischen Stelle (liegt dort ein lokales Maximum, ein lokales Minimum, oder ein Sattelpunkt vor?) kann man manchmal die Hesse-Matrix \(\Hesso{f}{\binom xy}\) benutzen. (Diese enthält in systematischer Weise die partiellen Ableitungen der Komponenten des Gradienten, also alle zweiten partiellen Ableitungen der Funktion \(f\) an der Stelle \(\binom xy.\))
In unserem Fall würde aber diese Hesse-Matrix an der Stelle \(P_0\) überhaupt nichts helfen: Eine listige Überlegung lehrt, dass \(\Hesso{f}{\binom00}\) die Nullmatrix ist.
Wir verfolgen stattdessen den Verlauf der Funktion, wenn wir uns entlang der Koordinatenachsen bzw. entlang der Winkelhalbierenden im Definitionsbereich bewegen (man kann sich das so veranschaulichen, dass wir entlang dieser Geraden jeweils einen vertikalen Schnitt durch den Funktionsgraph legen und die dann entstandene Kurve untersuchen).
Dazu betrachten wir die Hilfsfunktionen
\( \xi \colon \RR\to\RR \colon t\mapsto f\binom t0 = -\frac{t^4}4 \) (Betrachtung entlang der \(x\)-Achse),
\( \eta \colon \RR\to\RR \colon t\mapsto f\binom 0t = -\frac{t^4}4 \) (Betrachtung entlang der \(y\)-Achse),
\( h \colon \RR\to\RR \colon t\mapsto f\binom tt \) \( = (1-2t^2)t^4-\frac{t^4}2 \) \( = (\frac12-2t^2)t^4 \) \( = -2t^6+\frac12t^4 \) (Betrachtung entlang der ersten Winkelhalbierenden).
Die beiden Funktionen \(\xi\) und \(\eta\) nehmen bei \(t=0\) (also beim Durchgang durch \(P_0\) entlang einer der beiden Koordinatenachsen) offenbar ihr jeweiliges Maximum an: Größer als \(0 = \xi(0) =\eta(0)\) wird kein Funktionswert von \(\xi\) oder \(\eta.\)
Allein aus dem Verlauf der Funktion \(f\) entlang der Koordinatenachsen können wir also nicht erkennen, ob bei \(P_0\) ein lokales Maximum oder aber ein Sattelpunkt vorliegt.
Die Funktion \(h\) aber nimmt bei \(t=0\) ein lokales Minimum an!
Um das einzusehen, betrachten wir Ableitungen: Es gilt
\( h'(t) = -12t^5+2t^3,\)
\( h''(t) = -60t^4+6t^2,\)
\( h'''(t) = -240t^3+12t,\)
\( h''''(t) = -720t^2+12.\)
Für \(t=0\) erhalten wir \(0 = h'(0) = h''(0) = h'''(0),\) aber \(h''''(0)=12\) ist positiv: Damit ist nachgewiesen, dass \(h\) an der Stelle \(t=0\) ein lokales Minimum annimmt.
Es folgt, dass die Funktion \(f\) an der Stelle \(P_0\) weder ein lokales Maximum noch ein lokales Minimum annimmt: Es liegt ein Sattelpunkt vor.
Es sei \(R\) eine positive Zahl. Dann beschreibt die Ungleichung \(x^2+y^2 \leqq R^2\) die Menge \(D_R\) aller Punkte, die im Innern oder auf dem Rand des Kreises mit Radius \(R\) um den Ursprung liegen.
Diese Menge \(D_R\) ist kompakt (d.h., beschränkt und abgeschlossen), die Einschränkung \(f|_{D_R}\) der stetigen Funktion \(f\) auf \(D_R\) nimmt daher einen maximalen Wert \(M_R \coloneqq \max\set{f\binom xy}{\binom xy\in D_R}\) und einen minimalen Wert \(m_R \coloneqq \min\set{f\binom xy}{\binom xy\in D_R}\) an.
Für \(R\gt2\) gilt \(R^2-\frac32\gt0.\) Für jede Stelle \(Q = \binom xy\) auf dem Rand von \(D_R\) gilt \(x^2+y^2=R^2\) und (wegen \(R^2-\frac32\gt0\)) dann
\( (R^2-1)x^2y^2+\dfrac{x^4+y^4}4 \) \( {}= \) \( (R^2-\frac32)x^2y^2 + \dfrac{x^4+2x^2y^2+y^4}4 \) \( {}= \) \( (R^2-\frac32)x^2y^2 + \dfrac{(x^2+y^2)^2}4 \) \( {}\geqq \dfrac{R^4}4. \)
Daraus folgt \(f(Q) \leqq -\frac{R^4}4.\)
Jedenfalls erhalten wir \(m_R\leqq-\frac{R^4}4 \lt0.\) Da für jedes \(j\in\{1,2,3,4\}\) der Funktionswert \(f(P_j) = \frac1{6^3}\) positiv (und also größer als jeder auf dem Rand von \(D_R\) von \(f\) angenommene Wert) ist, kann der maximale Wert \(M_R\) nicht auf dem Rand der kompakten Menge \(D_R\) angenommen werden.
Es bleibt nur, dass \(M_R\) an einer (und dann an jeder) der kritischen Stellen \(P_1,\) \(P_2,\) \(P_3,\) \(P_4\) angenommen wird. Also gilt \(M_R=\frac1{6^3}\) für jede Zahl \(R\gt2.\)
Da sich für jede genügend große Zahl \(R\) ergeben hat, dass das Maximum \(M_R\) bei den kritischen Stellen \(P_1,\) \(P_2,\) \(P_3,\) \(P_4\) angenommen wird, liegen an diesen Stellen nicht nur lokale, sondern tatsächlich globale Maxima vor.
Wir haben alle kritischen Stellen der Funktion \(f\) bestimmt und auch deren Typ ermittelt: Es gibt vier lokale (und sogar globale) Maxima (die bei den kritischen Stellen \(P_1,\) \(P_2,\) \(P_3,\) \(P_4\) angenommen werden) und einen Sattelpunkt (bei \(P_0\)).
Insbesondere gibt es keine lokalen (und schon gar keine globalen) Minima der Funktion \(f.\)
Weiter oben wurde behauptet, die Hesse-Matrix an der Stelle \(\binom00\) sei die Nullmatrix. Das kann man natürlich durch Berechnung der partiellen Ableitungen der beiden Einträge im Gradienten herausfinden.
Es gibt auch ein schnelles, theoriebasiertes Argument: Wir betrachten Taylor-Entwicklungen. Da die Funktion \(f\) ein Polynom (in zwei Variablen) vom Totalgrad \(6\) ist, stimmt \(f\) mit dem Taylor-Polynom sechster Stufe im Entwicklungspunkt \(\binom00\) überein: Es gilt
\( f\binom xy = T_6^{}\left(f,\binom xy,\binom00\right) \) \( {} = {} \) \( x^2y^2-\frac14x^4-\frac14y^4 -x^4y^2-x^2y^4 .\)
Durch Weglassen von Termen höherer Ordnung
erhalten wir
z.B.
\( T_4^{}\left(f,\binom xy,\binom00\right) \) \( {} = x^2y^2-\frac14x^4-\frac14y^4 ,\)
und dann auch
\( T_2^{}\left(f,\binom xy,\binom00\right) \) \( {} = 0 \)
– alle Terme hatten höhere Ordnung als \(2.\)
Da sich das Taylorpolynom zweiter Stufe auch mit Hilfe des Funktionswerts, des Gradienten und der Hesse-Matrix am Entwicklungspunkt ergibt als
\( T_2^{}\left(f,\binom xy,\binom00\right) \) \( {} = \) \( f\binom00 + \nabla f\binom00\bullet\binom xy + \frac12\binom xy\transp\Hesso{f}{\binom00}\binom xy ,\)
erkennen wir, dass \(\Hesso{f}{\binom00} = \left(\begin{smallmatrix}0&0\\0&0\end{smallmatrix}\right).\)
Diese Hesse-Matrix hilft nicht bei der Frage, ob an der kritischen Stelle \(\binom00\) ein Extremum oder ein Sattelpunkt vorliegt.
Die bisher betrachtete Funktion ist ein Spezialfall (für \(c=\frac14\)) aus der Funktionenschar
\( f_c \colon \RR^2\to\RR \colon \) \( \binom xy\mapsto \) \( (1-x^2-y^2)x^2y^2-c(x^4+y^4) ,\)
hier ist \(c\in\RR\) als Parameter eingebaut.
Für negative Werte von \(c\) wird die Suche nach kritischen Stellen von \(f_c\) kompliziert, wir wollen hier davon die Finger lassen.
Für \(c=0\) passiert etwas Besonderes: Die Nullstellenmenge \(N\) von \(f_0\) ist die Vereinigung des Kreises mit Radius \(1\) um den Ursprung (die Lösungsmenge von \(1-x^2-y^2=0\)) mit den beiden Koordinatenachsen.
Im Innern \(D\) des Einheitskreises sind die Funktionswerte von \(f_0\) nie negativ. Also liegt an jeder Stelle im Schnitt \(N\cap D\) ein relatives Minimum von \(f_0\) vor.
Weil die abgeschlossene Kreisscheibe \(\overline{D}\) kompakt (und die Funktion \(f_0\) stetig) ist, nimmt die Funktion \(f_0\) in \(\overline{D}\) auch Maxima an.
Die fraglichen Stellen müssen sich wie oben unter den kritischen Stellen finden, an denen der Gradient \(\nabla f_0\binom xy\) Null wird. Es ergibt sich \(\nabla f_0\binom xy = 2xy \left( \begin{array}{c} y(1-2x^2-y^2) \\ x(1-x^2-2y^2) \end{array} \right)\).
Da uns Stellen auf den Koordinatenachsen nicht interessieren (dort gilt \(f_0\binom xy = 0\), und es wird sicher keines der Maxima in \(\overline{D}\) vorliegen), können wir \(xy\ne0\) annehmen. Dann ergeben sich die Bedingungen
\( \begin{array}{rcl} 1-2x^2-y^2 &=& 0 \\ \mbox{und } 1-x^2-2y^2 &=& 0 \,, \end{array} \)
daraus \(x^2=y^2\) und schließlich \(x^2=\frac13\).
Wir erhalten die vier kritischen Stellen \(Q_1 \coloneqq \frac1{\sqrt3}\binom{1}{1}\), \(Q_2 \coloneqq \frac1{\sqrt3}\binom{1}{-1}\), \(Q_3 \coloneqq \frac1{\sqrt3}\binom{-1}{1}\) und \(Q_4 \coloneqq \frac1{\sqrt3}\binom{-1}{-1}\).
Jede dieser Stellen liegt jedenfalls innerhalb des Einheitskreises; der Funktionswert \(f_0(Q_k) = \frac1{27}\) ist immer derselbe. Wir haben damit die vier Maximalstellen gefunden.
Außerhalb des Einheitskreises sind die Funktionswerte negativ an allen Stellen, die nicht auf den Koordinatenachsen liegen. An den Stellen auf den Achsen außerhalb des Kreises liegen also relative Maxima von \(f_0\) vor.
An den Schnittpunkten des Einheitskreises mit den Achsen finden wir Sattelpunkte, weil in beliebiger Nähe zu einem solchen Schnittpunkt sowohl Stellen mit positivem Funktionswert als auch Stellen mit negativem Funktionswert liegen.
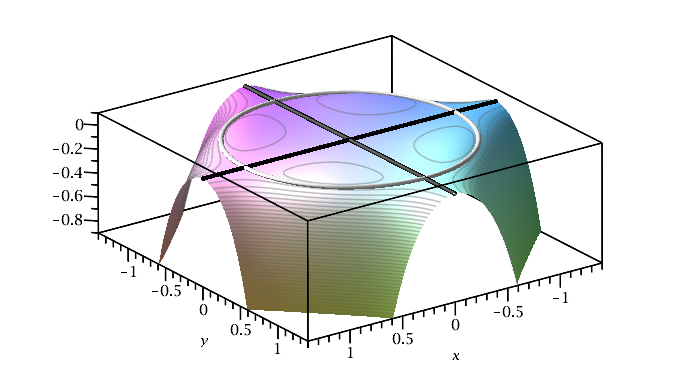
Für positive Werte von \(c\) können wir die Argumente von oben im Wesentlichen imitieren, wir erhalten für \(f_c\) jedenfalls die kritische Stelle \(P_0=\binom00,\) und vier weitere kritische Stellen \( P_1 \coloneqq u\binom{1}{1}, \) \( P_2 \coloneqq u\binom{1}{-1}, \) \( P_3 \coloneqq u\binom{-1}{1}, \) \( P_4 \coloneqq u\binom{-1}{-1}, \) wenn es eine reelle Zahl \(u\gt0\) mit \(u^2 = \frac{1-2c}3 \) gibt. Das ist genau dann der Fall, wenn \(c\lt\frac12\) gilt.
Wie oben (im Fall \(c=\frac14\)) ergibt sich, dass an diesen Stellen absolute Maxima der Funktion \(f_c\) angenommen werden, während bei \(P_0\) ein Sattelpunkt vorliegt.
Für \(c\geqq\frac12\) gibt es nur noch eine kritische Stelle für die Funktion \(f_c\) (nämlich \(P_0=\binom00.\) An dieser Stelle liegt dann ein lokales Maximum vor.
In der Tat ist \(P_0\) die einzige Nullstelle der Funktion \(f_c\) wenn \(c\geqq{\frac12};\) an allen anderen Stellen ist der Funktionswert \(f_c \binom xy \) \( = \) \( -\frac12(x^2-y^2)^2-x^2y^2(x^2+y^2) \) \( -(c-\frac12)(x^4+y^4) \) negativ. Also ist das Maximum sogar absolut.
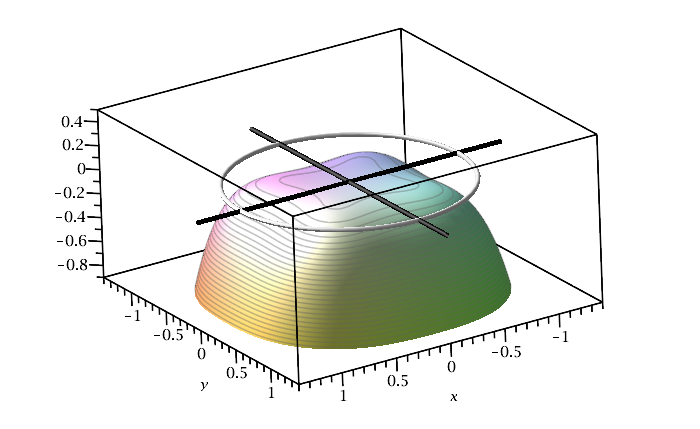
Das Schaubild zeigt einen Ausschnitt aus dem Graphen von \(f_{\frac12}.\)
Wenn man sich ein Herz fasst, ist die Bestimmung der Hesse-Matrix doch nicht so fürchterlich – allerdings an der Stelle \(\binom00\) eben leider überhaupt nicht hilfreich. Für die anderen kritischen Stellen trägt die Hesse-Matrix aber wenigstens teilweise die gesuchte Information, deswegen berechnen wir diese Matrix jetzt.
Wir betrachten wieder
\(
f_c \colon \RR^2\to\RR \colon
\)
\(
\binom xy\mapsto
\)
\(
(1-x^2-y^2)x^2y^2-c(x^4+y^4)
,\)
mit \(c\in\RR.\)
Es gilt \( f_c \binom xy \) \( = (1-x^2-y^2)x^2y^2-c(x^4+y^4) \) \( = \) \( x^2y^2-c(x^4+y^4) - x^4y^2-x^2y^4 ,\)
also \(\displaystyle \nabla f_c\binom xy \) \( = \) \(\displaystyle \binom{2xy^2-4cx^3-4x^3y^2-2xy^4}{2x^2y-4cy^3-2x^4y-4x^2y^3} \)
und \(\displaystyle \Hesso{f_c}{\binom xy} \) \( = \) \( \left( \begin{matrix} 2y^2-12cx^2-12x^2y^2-2y^4 & 4xy-8x^3y-8xy^3 \\ 4xy-8x^3y-8xy^3 & 2x^2-12cy^2-2x^4-12x^2y^2 \end{matrix} \right) .\)
Wie prophezeit, gilt \(\Hesso{f_c}{\binom00} = \left(\begin{smallmatrix}0&0\\0&0\end{smallmatrix}\right).\) Hier bringt uns die Hesse-Matrix also keine Information.
Für \(c\lt0\) scheuen wir die Bestimmung der kritischen Stellen, und für \(c\geqq\frac12\) gibt es nur die eine kritische Stelle \(P_0=\binom00\), an der die Hesse-Matrix nicht hilft. Deswegen können wir uns auf den Fall \(0\leqq c\lt\frac12\) konzentrieren. Den Spezialfall \(c=0\) haben wir auch schon komplett diskutiert.
Jetzt nehmen wir \(c\gt0\) an. Wenn es eine reelle Zahl \(u\gt0\) mit \(u^2 = \frac{1-2c}3 \) gibt (also genau dann, wenn \(c\lt\frac12\) gilt), erhalten wir – außer \(P_0\) – noch die kritischen Stellen \( P_1 \coloneqq u\binom{1}{1}, \) \( P_2 \coloneqq u\binom{1}{-1}, \) \( P_3 \coloneqq u\binom{-1}{1}, \) \( P_4 \coloneqq u\binom{-1}{-1}. \)
Mit \(c=\frac{1-3u^2}2\) ergibt sich
\( \Hesse{f_c}{P_1} = \Hesse{f_c}{P_4} \) \( = 2u^2\left( \begin{matrix} 1-6c-7u^2 %%% = 2u^2-12cu^2-12u^4-2u^4 & 2-8u^2 %%% 2u^2-4u^4-4u^4 \\ 2-8u^2 %%% 2u^2-4u^4-4u^4 & 1-6c-7u^2 %%% u^2-6cu^2-u^4-6u^4 \end{matrix} \right) \) \( = 4u^2\left( \begin{matrix} u^2-1 & 1-4u^2 \\ 1-4u^2 & u^2-1 \end{matrix} \right) \)
und analog
\( \Hesse{f_c}{P_2} = \Hesse{f_c}{P_3} \) \( = 2u^2\left( \begin{matrix} 1-6c-7u^2 % & -2+8u^2 \\ -2+8u^2 & 1-6c-7u^2 \end{matrix} \right) \) \( = 4u^2\left( \begin{matrix} u^2-1 & -1+4u^2 \\ -1+4u^2 & u^2-1 \end{matrix} \right) .\)
Für jedes \(j\in\{1,2,3,4\}\) gilt damit \( \det\Hesse{f_c}{P_j} \) \( = 16u^4\bigl( (u^2-1)^2-(1-4u^2)^2 \bigr) \) \( = 16u^6 \left( 6-15u^2 \right) \) \( = 48u^6(2-5u^2) .\)
Wegen \(0\lt c\lt\frac12\) gilt \(0\lt u^2\lt\frac13,\) und mit \(\frac13\lt\frac25\) erkennen wir, dass \(\det\Hesse{f_c}{P_j}\) für jedes \(j\in\{1,2,3,4\}\) positiv ist. Also haben die beiden Eigenwerte der Hesse-Matrix \(\Hesse{f_c}{P_j}\) das gleiche Vorzeichen.
Da die Spur \(4u^2(2u^2-2)\) der Hesse-Matrix \(\Hesse{f_c}{P_j}\)
jeweils (wegen \(u^2\lt\frac13\lt1\)) negativ ist, sind beide Eigenwerte negativ. Also ist die
Hesse-Matrix an jeder der vier betrachteten kritischen Stellen
negativ definit, und verrät uns damit, dass an diesen Stellen lokale
Maxima vorliegen.
(Wer mit Gewalt die Eigenwerte explizit ausrechnet, kommt auf
\(5u^2-2\) und \(-3u^2.\))
Grundsätzlich kann die Hesse-Matrix nicht erkennen, ob ein lokales Maximum global ist. Für die hier vorliegenden Stellen wissen wir aus unseren Überlegungen weiter oben, dass globale Maxima vorliegen.
Da die zu Beginn betrachtete Funktion \(f\) gerade \(f_c\) mit \(c=\frac14\) (also mit \(0\lt c\lt\frac12\)) war, können wir zur Veranschaulichung unserer letzten Ergebnisse die Skizze vom Anfang recyceln:

Die Fotografien sind eigenes Werk des Autors, bzw.
Fotografien von David Zimmer (wie angegeben), bearbeitet durch den
Autor.
Die Grafiken wurden vom Autor erstellt mit Hilfe von
Maple (2020.2).