| ↰ 5.1 | Material | |
| ← 5.3 | HM 2 |
Wenn wir eine reellwertige Funktion in \(n\) Veränderlichen über eine Kurve in \( \RR^n \) integrieren wollen, brauchen wir nicht wie in 5.3.1 durch ein Skalarprodukt einen reellen Integranden zu erzeugen.
Stattdessen integrieren wir das Produkt der Funktion mit dem Betrag des Geschwindigkeitsvektors (also der Ableitung der Parametrisierung) beim betreffenden Punkt auf der Kurve:
Es sei \( D=\inn D\subseteq\RR^n \) und \( C\colon[a,b]\to D \) eine reguläre und doppelpunktfreie Parametrisierung einer Kurve \(K\) in \(D\).
Außerdem betrachten wir eine Funktion \( f\colon K\to\RR \) derart, dass die Komposition \( f\circ C\colon [a,b]\to\RR \) stetig ist (das ist sicher der Fall, wenn \(f\) durch Einschränkung einer auf \(D\) stetigen Funktion entsteht).
Dann heißt
\( \alert{\int_K f(s)\,\diff s} \) \( := \ds\int_a^b f\bigl(C(t)\bigr) \, |C'(t)|\,\diff t \)
das Kurvenintegral von \(f\) längs \(K\).
Hier ist \(s\) zu interpretieren als ein Punkt, der sich längs \(K\) bewegt.
Das Symbol
\( \diff s \)
nennt man skalares Bogenelement.
Die Länge einer Kurve \(K\) bestimmt man mit Hilfe einer regulären und doppelpunktfreien Parametrisierung \( C\colon[a,b]\to K \) als
\( \alert{L(K)} \) \( := \ds\int\limits_K 1 \,\diff s \) \( = \ds\int_a^b |C'(t)|\,\diff t \).
Auch dieses Kurvenintegral einer reellwertigen Funktion hängt nicht von der Parametrisierung der Kurve ab [weil diese doppelpunktfrei ist].
Im Unterschied zum Kurvenintegral in 5.3.1 hängt das jetzt betrachtete Integral auch nicht vom Durchlaufungssinn ab.
Weil wir den Betrag der Ableitung \( C' \) verwenden.
Bei Umlaufintegralen muss man die Unabhängigkeit von der Parametrisierung der (dann geschlossenen) Kurve präzisieren:
Es seien \( B\colon[u,v]\to K \) und \( C\colon[a,b]\to K \) reguläre Parametrisierungen einer geschlossenen Kurve \(K\) mit \(B ( u ) = B ( v )\) und \(C ( a ) = C ( b )\).
Wird die Kurve bei beiden Parametrisierungen gleich oft durchlaufen (sind also für jedes \( t_0^{}\in[a,b] \) die Mengen \( \bigset{t\in(a,b)}{C(t)=\color{blue}{C(t_0^{})}} \) und \( \bigset{\color{red}{\tilde{t}}\in(u,v)}{\color{red}{B(\tilde{t})}=\color{blue}{C(t_0^{})}} \) gleich groß), so gilt
\( \ds\int_a^b f\bigl(C(t)\bigr)\,|C'(t)|\,\diff t \) \( = \ds\int_u^v f\bigl(B(\tilde{t})\bigr)\,|B'(\tilde{t})|\,\diff\tilde{t} \).
Wenn man die Länge \( L(K) \) der Kurve \(K\) kennt, kann man aus \( \color{blue}{\frac1{L(K)}} \) \( \color{blue}{ \ds\int_a^b |C'(t)|\,\diff t} \) die Anzahl der Umläufe um \(K\) ermitteln.
Es sei \(K\) eine regulär parametrisierbare Kurve, und es seien \(f\) und \(g\) stetige Funktionen auf \(K\). Dann gilt für alle \( c\in\RR \):
Zu jeder regulär und doppelpunktfrei parametrisierbaren Kurve \(K\) und jeder auf \(K\) stetigen Funktion \(f\) gibt es einen Punkt \( m\in K \) derart, dass gilt:
\( \int_K f(s)\,\diff s = f(m) \, L(K) \).
Das Kurvenintegral
\(
\)
einer reellwertigen Funktion beschreibt die Fläche
eines Zaunes
, der entlang der Kurve errichtet ist:
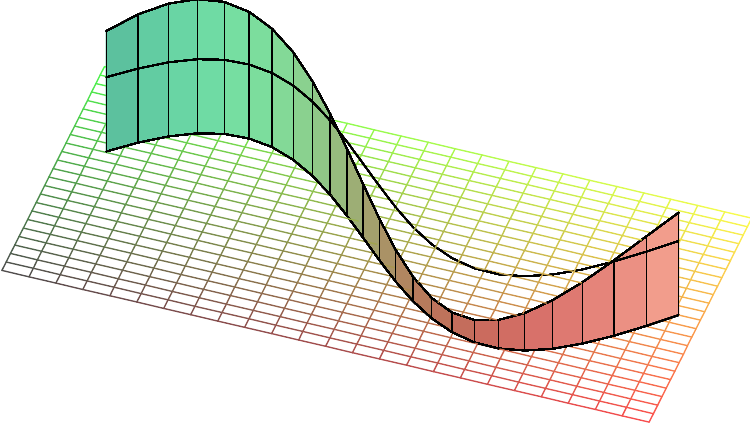
Die Höhe des Zauns im Punkt \( P\in K \) ist dabei \( f(P) \).
Der Mittelwertsatz besagt nicht nur, dass man den Zaun durch einen Zaun konstanter Höhe ersetzen kann, ohne die Fläche zu ändern, sondern dass diese konstante Höhe unter den Funktionswerten vorkommt.
Die mittlere Höhe ist in der Skizze ebenfalls eingezeichnet, die Funktion \(f\) nimmt diese Höhe zweimal an.
Es sei \( K\subseteq\RR^n \) eine Kurve mit regulärer und doppelpunktfreier Parametrisierung \( C\colon[a,b]\to K \).
Dann ist der normierte Tangentenvektor \( \frac{C'(t)}{|C'(t)|} \) bis auf sein Vorzeichen unabhängig von der Wahl der Parametrisierung.
Für jedes stetige Vektorfeld \( g\colon D\to\RR^n \), dessen Definitionsbereich \(D\) die Kurve \(K\) enthält, definiert \( f\bigl(C(t)\bigr) := \) \( g\bigl(C(t)\bigr)\skalp\frac{C'(t)}{|C'(t)|} \) eine reellwertige Funktion \( f\colon K\to\RR \), die man skalare Tangentialkomponente des Feldes nennt.
Es gilt
\( \ds\int_K f(s)\,\diff s \) \( = \ds\int_a^b g\bigl(C(t)\bigr)\skalp\frac{C'(t)}{|C'(t)|}\,|C'(t)| \,\diff t \) \( = \ds\int_a^b g\bigl(C(t)\bigr)\skalp C'(t)\,\diff t \) \( = \ds\int_K g(x)\skalp\diff x \).
Wir beschreiben eine ebene Strömung durch ihr Geschwindigkeitsfeld:
Dies ist ein Vektorfeld \( g\colon D\to\RR^2 \) mit \( D\subseteq\RR^2 \).
Wir wollen berechnen, wieviel (Volumen pro Zeiteinheit) der Flüssigkeit oder des Gases aus dem durch eine geschlossene Kurve begrenzten Teil herausfließt (Ausfluss durch \(K\)) und wieviel an der Kurve entlang fließt (Zirkulation längs \(K\)).
Wir benutzen eine doppelpunktfreie und stückweise reguläre Parametrisierung
\( C\colon[a,b]\to K\colon{}\pause t\mapsto C(t) \) \( = \left( \begin{array}{c} C_1^{}(t) \\ C_2^{}(t) \end{array}\right) \)
und zerlegen den Vektor \( g(P) \) an jedem Punkt \( P=C(t) \) der Kurve in die Komponenten in Tangentenrichtung \( \frac1{|C'(t)|}\,C'(t) \) bzw. orthogonal dazu, also in Richtung des Normalenvektors \( n(t):= \) \( \frac1{\sqrt{\bigl(C_2'(t)\bigr)^2 + \bigl(C_1'(t)\bigr)^2}} \, \left( \begin{array}{r} C_2'(t) \\ - C_1'(t) \end{array} \! \right) \) \( =\frac1{|C'(t)|} \, \left( \begin{array}{r} C_2'(t) \\ - C_1'(t) \end{array} \right) \).
Was uns wirklich interessiert, ist jeweils die orientierte Länge dieser Komponenten, diese erhalten wir als Skalarprodukt:
\( \alert{T\bigl(C(t)\bigr)} \) \( := g\bigl(C(t)\bigr)\skalp \frac1{|C'(t)|}\,C'(t) \)
bzw.
\( \alert{N\bigl(C(t)\bigr)} \) \( := g\bigl(C(t)\bigr)\skalp n(t) \).
Man nennt
\( \alert{Z(g,K)} \) \( := \ds\int_K T(s)\,\diff s \) \( = \ds\int_a^b T\bigl(C(t)\bigr)\,|C'(t)| \,\diff t \) \( = \ds\int_a^b g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t \)
die Zirkulation von \(g\) längs \(K\)
bzw.
\( \alert{A(g,K)} \) \( := \ds\int_K N(s)\,\diff s \) \( = \ds\int_a^b N\bigl(C(t)\bigr)\,|C'(t)| \,\diff t \) \( = \) \( \ds\int_a^b g\bigl(C(t)\bigr)\skalp \left( \begin{array}{r} C_2'(t) \\ - C_1'(t) \end{array} \! \right) \,\diff t \)
den Ausfluss von \(g\) durch \(K\).
Der Mittelwertsatz 5.4.6 liefert die Existenz von Stellen \( \color{darkviolet}{m_T} \) und \( \color{blue}{m_N} \) auf der Kurve \(K\) mit \( \int_K T(s)\,\diff s \) \( =T(\color{darkviolet}{m_T^{}})\,L(K) \) und \( \int_K N(s)\,\diff s \) \( =N(\color{blue}{m_N^{}})\,L(K) \).
Wir können etwa \( N(\color{blue}{m_N^{}}) \) interpretieren als mittleren Ausfluss durch \(K\).
Wann immer ein (skalarer oder vektorieller) Wert sich kontinuierlich verändert — also in stetiger Abhängigkeit von einem reellen Parameter — kann man zur Mittelbildung nicht einfach die Definition des arithmetischen Mittelwerts benutzen: Man müsste ja unendlich viele Werte aufaddieren.
Statt dessen ist es üblich, ein Integral (wie beim mittleren Ausfluss) zu benutzen. Die Rolle der Division durch die Anzahl der aufsummierten Werte übernimmt dann die Division durch die Länge des Parameterintervalls oder — wenn die Parametrisierung die Länge verändert — die Länge der Kurve, über die man integriert.
Hier ist wichtig, dass unsere Formeln für die Kurvenintegrale die Ableitung der Parametrisierung (also die Geschwindigkeit, mit der die Kurve durchlaufen wird) in geeigneter Weise berücksichtigen. Dass die Formeln dies richtig modellieren, ist auch wesentlich dafür, dass man wirklich die Länge der Kurve auf die in 5.4.2 angegebene Weise berechnen kann.
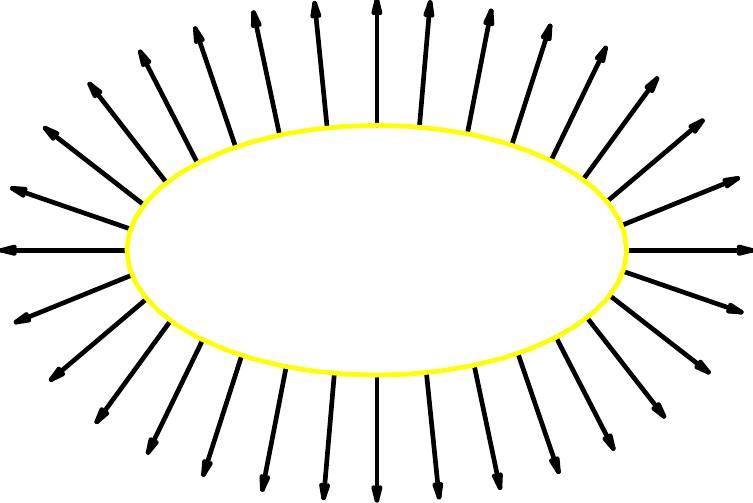
Wir parametrisieren eine Ellipse \(K\) durch
\( C\colon[0,2\,\pi]\to\RR^2\colon{} \) \( t\mapsto \left( \begin{array}{r} 2\,\cos t \\ \sin t \end{array}\right) \).
Dann gilt \( C'(t) = \left( \begin{array}{r} -2\,\sin t \\ \cos t \end{array}\right) \) und \( n(t) = \dfrac1{|C'(t)|}\,\left( \begin{array}{r} \cos t \\ 2\,\sin t \end{array}\right) \).
Das Normalenfeld \(n\) zeigt nach außen, weil die Kurve im mathematisch positiven Sinn (also gegen den Uhrzeigersinn) durchlaufen wird:
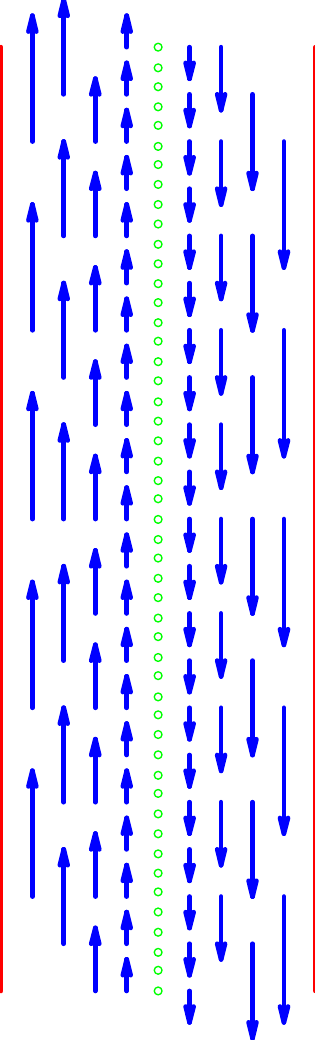
Das Geschwindigkeitsfeld der Strömung sei
\( g\colon \RR^2\to\RR^2\colon{} \) \( \left( \begin{array}{r} u \\ v \end{array}\right) \mapsto \left( \begin{array}{r} 0 \\ -u \end{array}\right) \).
Ein solches Feld kann etwa — näherungsweise — das Verhalten des Schmierfilms bei einer Gleitschmierung beschreiben:
Es handelt sich hier um eine sogenannte Couette-Strömung.
An jedem Punkt \(P = C ( t )\) der Ellipse zerlegen wir den Geschwindigkeitsvektor
\( \color{blue}{g(P)=g\bigl(C(t)\bigr)} \) in die Komponenten
\( \color{red}{g_T^{}(t)} \) \( := T\bigl(C(t)\bigr)\,\dfrac{C'(t)}{|C'(t)|} \) tangential und
\( \color{green}{g_N^{}(t)} \) \( = N\bigl(C(t)\bigr)\, n(t) \) orthogonal zur Kurve:
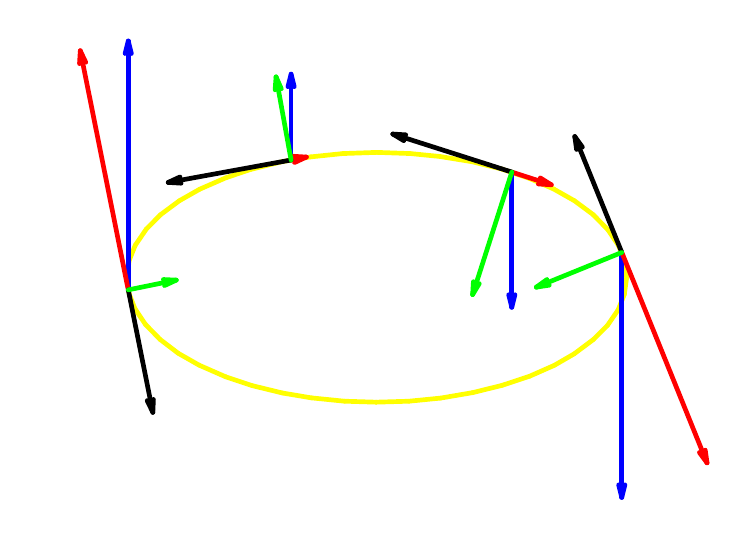
Die folgenden Skizzen zeigen das Geschwindigkeitsfeld an ausgewählten Punkten der Kurve sowie das Feld \( g_N^{} \):
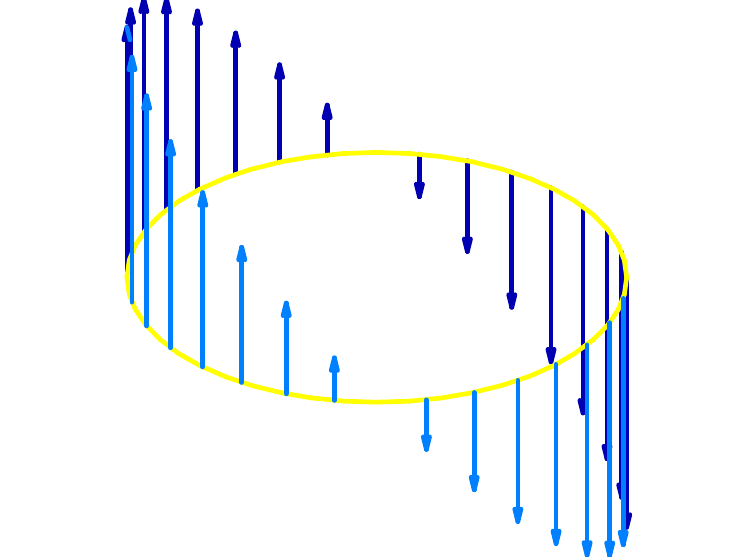
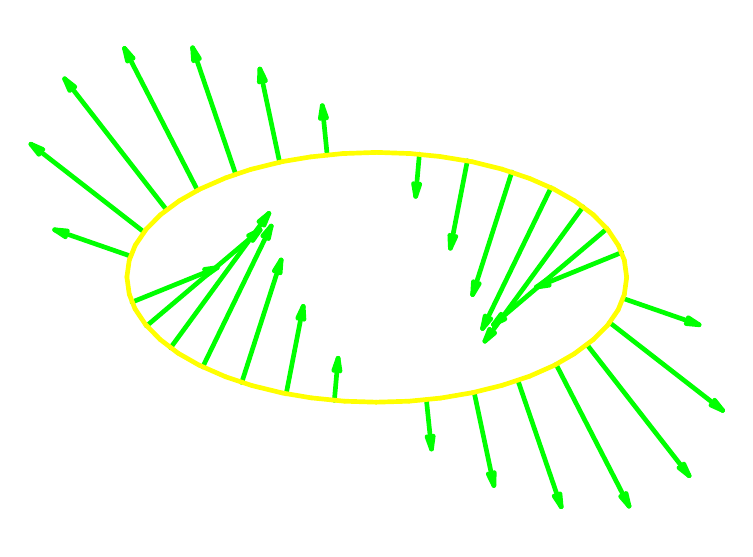
Der zur Tangente orthogonale Anteil des Flusses beschreibt den Ausfluss durch \(K\): Wir berechnen den Gesamtausfluss als
\( A(g,K) \) \( = \ds\int_K N(s)\,\diff s \) \( = \ds\int_a^b g\bigl(C(t)\bigr)\skalp \left( \begin{array}{r} C_2'(t) \\ - C_1'(t) \end{array} \right) \,\diff t \) \( = \ds\int_0^{2\,\pi} \left( \begin{array}{c} 0 \\ - 2\,\cos t \end{array}\right) \skalp \left( \begin{array}{r} \cos t \\ 2\,\sin t \end{array}\right) \,\diff t \) \( = 0 \).
Der Anteil des Flusses, der tangential zur Kurve läuft, liefert die Zirkulation von \(g\) längs \(K\):
\( Z(g,K) \) \( = \ds\int_K T(s)\,\diff s \) \( = \ds\int_a^b g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t \) \( = \ds\int_0^{2\,\pi} \left( \begin{array}{c} 0 \\ -2\,\cos t \end{array}\right) \skalp \left( \begin{array}{r} -2\,\sin t \\ \cos t \end{array}\right) \diff t \) \( = \ds\int_0^{2\,\pi} -2\,(\cos t)^2 \,\diff t \) \( = -2\,\pi \).
Man kann jetzt auch nachrechnen, dass sich die Zirkulation nicht ändert, wenn wir die Ellipse innerhalb des Gebiets der Couette-Strömung verschieben.
Die folgenden Skizzen zeigen das Tangentenfeld und den zirkulären Fluss \( g_T^{} \):

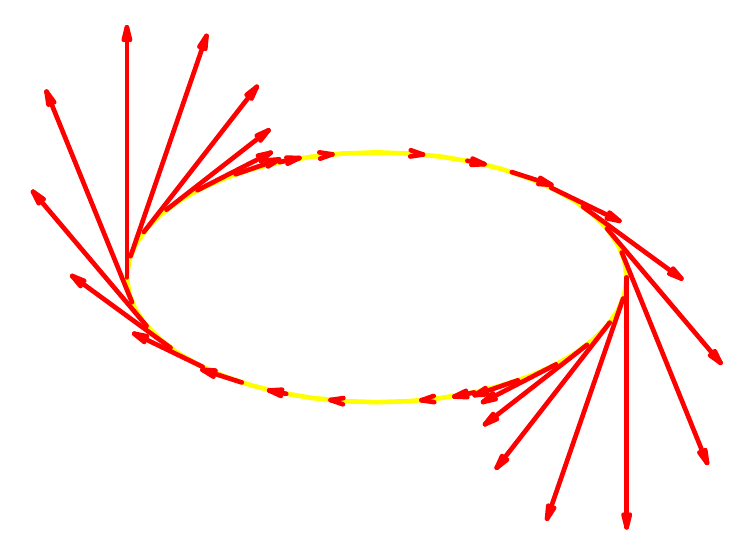
Der zirkuläre Fluss läuft im Uhrzeigersinn, also gegen das Tangentenfeld: das passt zum negativen Vorzeichen des berechneten Werts.
| ↰ 5.1 | Material | |
| ← 5.3 | HM 2 |