1.10. Stetigkeit

Wir betrachten im Folgenden Funktionen, die reellen Zahlen wieder reelle Zahlen zuordnen:
Also Abbildungen $f:M\to \mathbb{R}$ mit $M⫅\mathbb{R}$.

Jede solche Funktion kann man durch ihren Graph veranschaulichen: Man trägt $y=f(x)$ über $x$ auf, markiert also die Punkte mit Koordinaten $(x,f(x))$ für $x\in M$.

1.10.1. Beispiele.

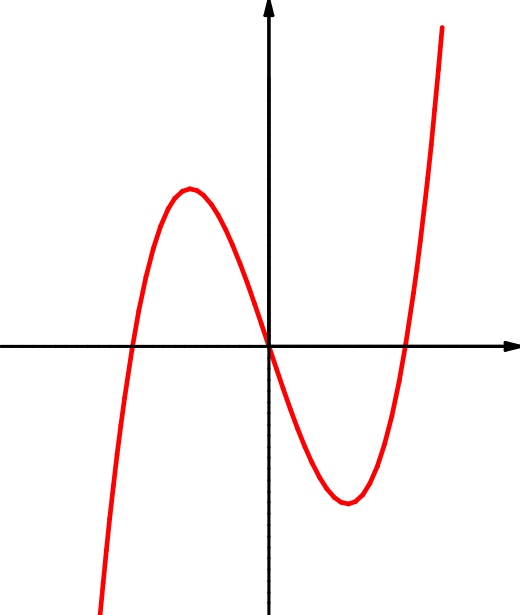
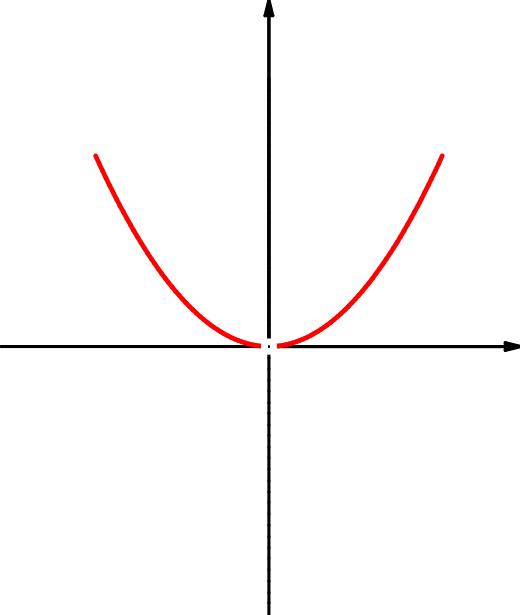
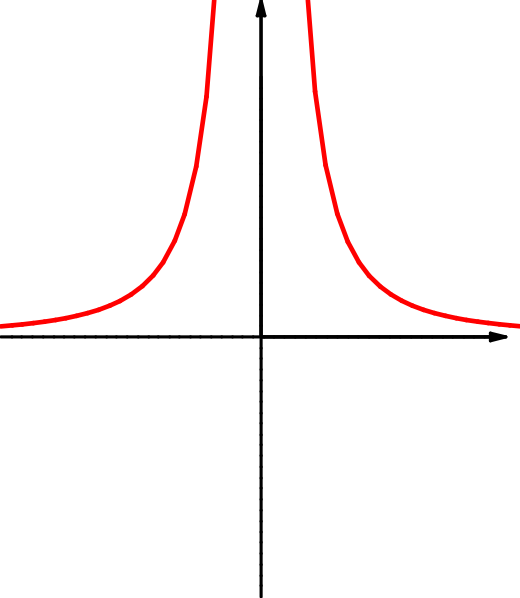
$f(x)=4x^3-3x$	$f(x)={\displaystyle \frac{x^3}{x}}$	$f(x)={\displaystyle \frac{1}{x^2}}$
$M=\mathbb{R}$	$M=\mathbb{R}\setminus \{0\}$	$M=\mathbb{R}\setminus \{0\}$

1.10.2. Beispiele.

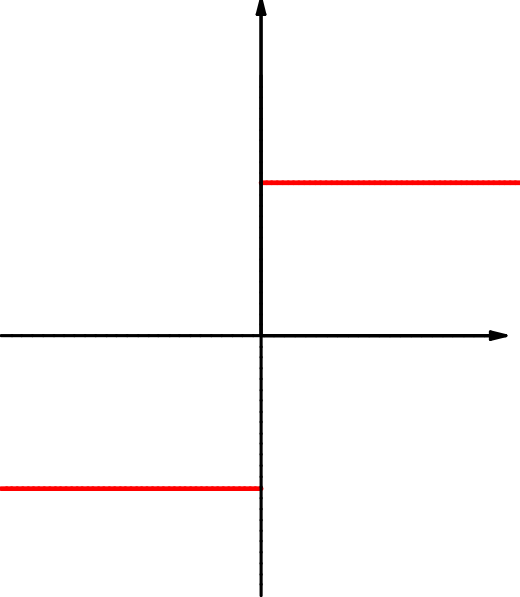
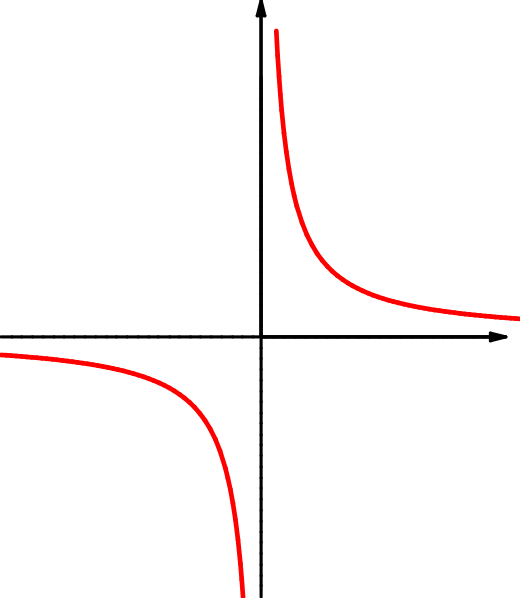
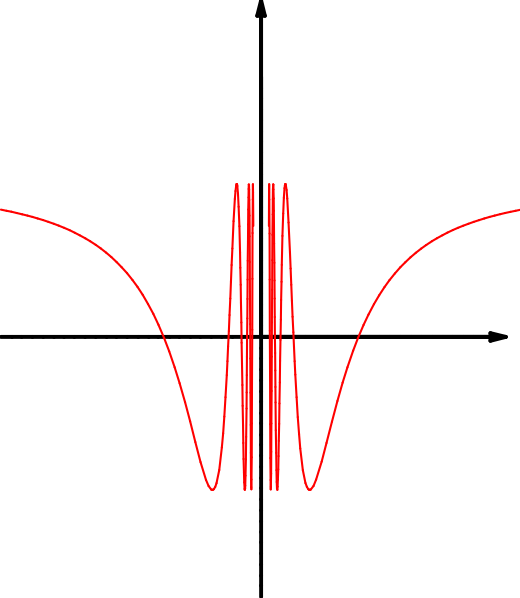
$f(x)={\displaystyle \frac{|x|}{x}}$	$g(x)={\displaystyle \frac{1}{x}}$	$h(x)=\cos ({\displaystyle \frac{1}{x}})$
$M=\mathbb{R}\setminus \{0\}$	$M=\mathbb{R}\setminus \{0\}$	$M=\mathbb{R}\setminus \{0\}$

Bei manchen dieser Beispiele weisen die Graphen „Lücken“ oder „Sprünge“ auf. Manche dieser Lücken kann man „sinnvoll“ durch Ergänzung schließen. Bei den Beispielen in 1.10.2 ist das aber nicht möglich. Wir wollen unser Gefühl präzisieren, das uns sagt, welche Ergänzung des Graphen „sinnvoll“ ist.

1.10.4. Beispiel.

Die Funktion $f:\mathbb{R}\to \mathbb{R}$ sei definiert durch

Diese Funktion ist nicht stetig in $x_0=0$, denn für die durch $x_j:=\frac{1}{j}$ definierte Folge gilt $x_j\underset{}{⟶}0$ und $f(x_j)\underset{}{⟶}0$, aber $0\ne 1=f(0)$. Es gibt aber viele andere gegen $0$ konvergente Folgen (z. B. ${\left(\frac{\pi }{j}\right)}_{j\in \mathbb{N}}$ für die die Folge der Funktionswerte gegen $f(0)$ konvergiert!

Es ist sehr schwer, alle Folgen in den Griff bekommen, die gegen eine Stelle $x_0$ konvergieren.
Die folgende Beschreibung wirkt erst einmal abschreckend, wird aber genau mit diesem fundamentalen Problem fertig:

1.10.5. Die $\epsilon$-$\delta$-Beschreibung der Stetigkeit.

Die Funktion $f:M\to \mathbb{R}$ ist genau dann stetig im Punkt $x_0$ wenn gilt:

Dabei wird zuerst die Fehlertoleranz $\epsilon$ vorgegeben: Die Schranke $\delta ={\delta }_{\epsilon }$ hängt von der Wahl von $\epsilon$ ab.

Man kann das auch so ausdrücken:

1.10.6. Beschreibung der Stetigkeit durch Umgebungen.

Die Funktion $f:M\to \mathbb{R}$ ist genau dann stetig im Punkt $x_0\in M$, wenn es zu jeder Umgebung $U=U_{\epsilon }(f(x_0))$ eine Umgebung $V=U_{\delta }(x_0)$ derart gibt, dass $f(V\cap M)⫅U$.

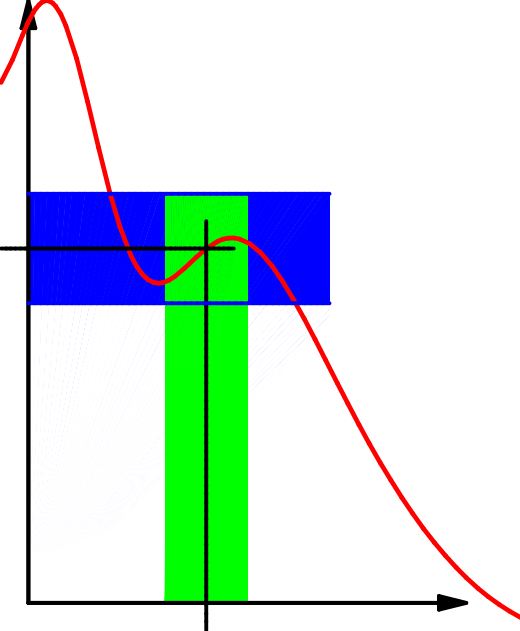
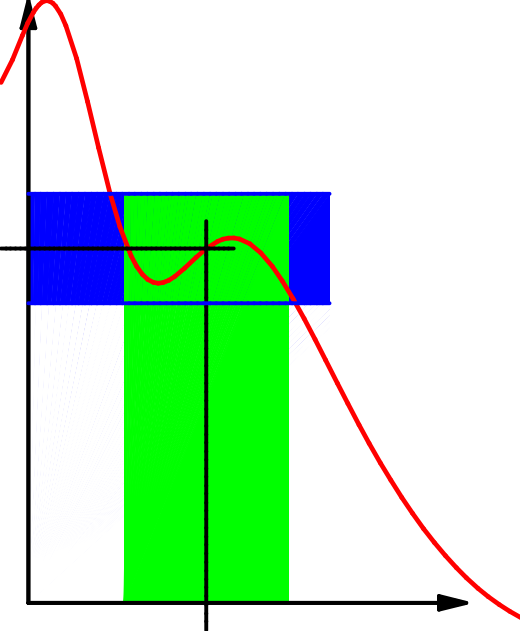
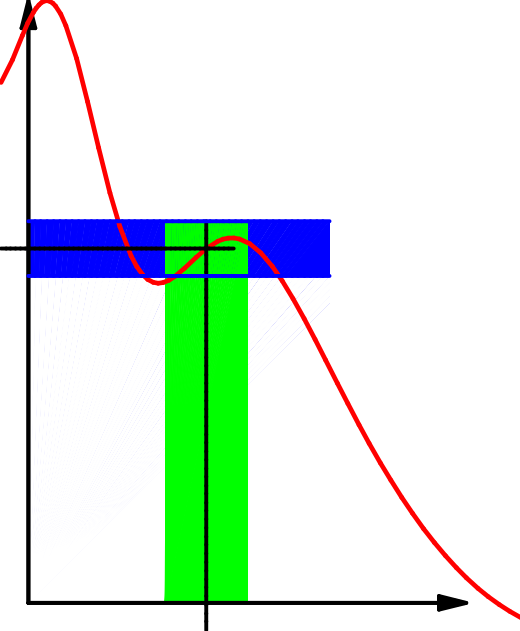
Die Beschreibung durch Umgebungen ist recht anschaulich:

$x_0$	$x_0$	$x_0$
Es gilt hier		aber
$f(U_{\delta }(x_0))⫅U_{\epsilon }(f(x_0))$;	$f(U_{2\delta }(x_0))⫅U_{\epsilon }(f(x_0))$;	$f(U_{\delta }(x_0))⊈U_{\frac{1}{2}\epsilon }(f(x_0))$.

Ihnen ist das nicht anschaulich genug?
(verständlich...)

Ein interaktives Spielzeug dazu finden Sie hier.