Interaktive Seiten

Ganz ohne Freude soll (und kann) man Mathematik nicht lernen - also folgen Sie den Links und lassen Sie Ihrem Spieltrieb mal freien Lauf: Multiplikation komplexer Zahlen in Polarkoordinaten Unstetigkeit des Wurzelziehens Eigenvektoren und Eigenwerte / Eigenvectors and Eigenvalues (English version) Hyperbolas defined by quadratic equations (English version) A quadric depending on a parameter (English version) Ableitung (Sekanten und Tangente an einer Hyperbel) Die englischen Versionen wurden erstellt für Studierende der University of Canterbury (Christchurch, NZ) während eines Aufenthalts als Visiting Erskine Fellow.

Ergänzungen zum Skript, Errata

zu Themen aus HM 1:

Für die Studierenden, die noch das (alte, gelbe) Buch „Lineare Algebra und Geometrie“ (von Kimmerle und Stroppel) benutzen, gibt es:

• Das im neuen Buch „Höhere Mathematik 1“ (2023) hinzugenommene Kapitel 2 („Folgen und Reihen“ — in der Vorlesung „HM 1“ war dieser Stoff seit 2005 enthalten).
• Den neuen Abschnitt 4.14 über den Einsatz der geometrischen Reihe zur näherungsweisen Bestimmung einer inversen Matrix.
• Den neuen Abschnitt 6.5 über den Einsatz von Eigenwerttheorie bei rekursiv definierten Folgen.
  Diese Version von Abschnitt 6.5 ist auch verbessert im Vergleich zur Version im ersten Druck der ersten Auflage (2023).

Praktische Bestimmung der Lösungen einer quadratischen Gleichung in komplexen Zahlen (mit vertieftem Hintergrundwissen)

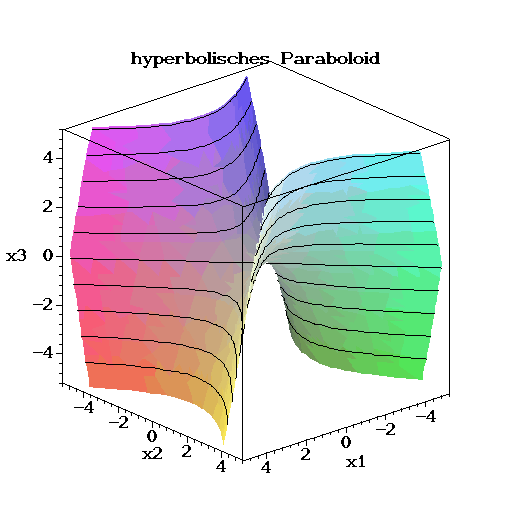
Seite mit Bildern von räumlichen Quadriken

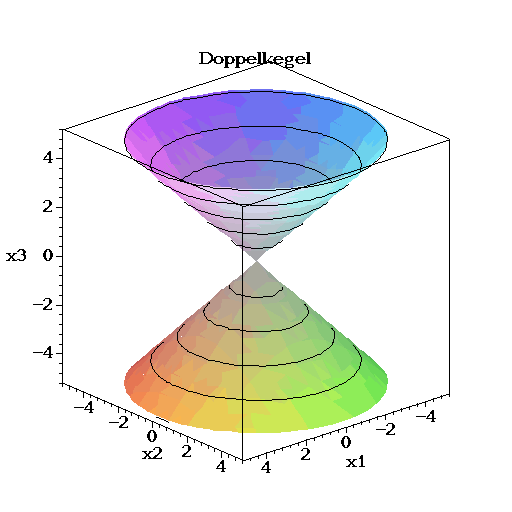
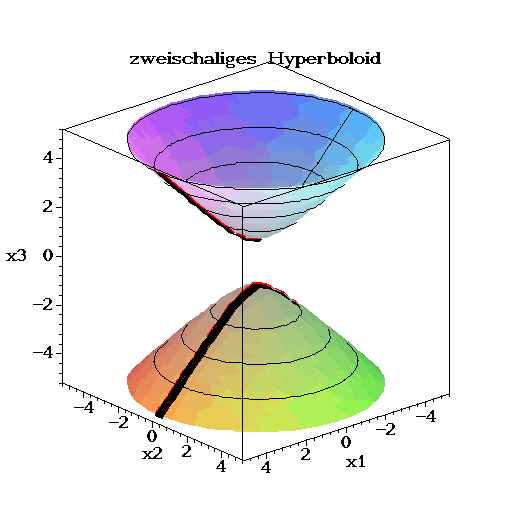
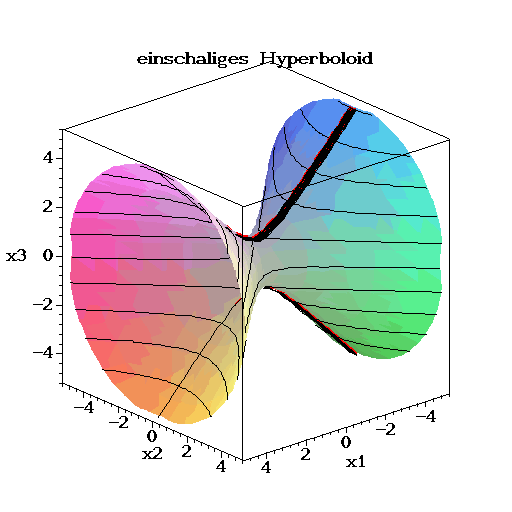
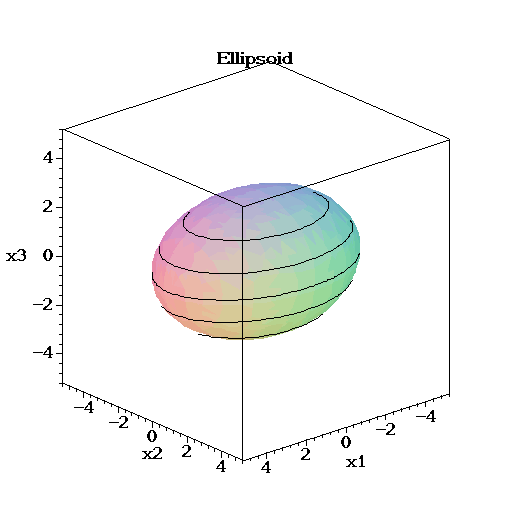
zu Themen aus HM 2:

Überraschungen bei lokalen Extrema – oder die Geschichten vom Affendach, dem Expowurm und von Zimmers Zeltdach:
Gibt es eine (differenzierbare) Funktion in zwei Veränderlichen, die zwar mehrere (lokale) Maxima, aber keine lokalen Minima hat?
(JA!)

Beispiele von Funktionen, bei der das Taylorpolynom zweiter Stufe keine Approximation zweiter Ordnung liefert:
Warum man sich bei der Suche nach Extrema wünscht, dass die betrachteten Funktionen zweimal stetig differenzierbar sind.

Eine Abhandlung zur Frage: Wie definiert man Null hoch Null?
(nebst einiger weiterer Bemerkungen zu Potenzrechengesetzen, Stetigkeit, stetiger Fortsetzbarkeit, Kommutativgesetz, Assoziativgesetz)

Eine Seite mit Bildern und Kommentaren zur Interpretation der Erdoberfläche als Funktionsgraph.

Zusätzlicher Stoff über Konvergenz in metrischen Räumen

(bisher sind noch keine Fehler in den Bänden „Höhere Mathematik 1“ und „Höhere Mathematik 2“ (edition delkhofen, 2023) bekannt.

Errata zu den älteren Büchern (Kimmerle-Stroppel, „Lineare Algebra und Geometrie“ und „Analysis“) finden Sie noch hier.

Ungewohnte Schriften

Viele mathematische Objekte werden mit griechischen Buchstaben oder mit alten deutschen Buchstaben bezeichnet. Hier sind saubere Darstellungen als Vorlage für Lese- und Schreibübungen zu erhalten:

• griechische Buchstaben
• Fraktur- und Sütterlin-Buchstaben

• M. Stroppel, Höhere Mathematik 1 für Ingenieure, Mathematiker und Physiker, Deilingen-Delkhofen: Ed. Delkhofen (als Skript zur Vorlesung geeignet). ISBN 978-3-936413-32-8.
• M. Stroppel, Höhere Mathematik 2 für Ingenieure, Mathematiker und Physiker, Deilingen-Delkhofen: Ed. Delkhofen (als Skript zur Vorlesung geeignet). ISBN 978-3-936413-40-3.
• W. Kimmerle, M. Stroppel, Lineare Algebra und Geometrie für Ingenieure, Mathematiker und Physiker, Deilingen-Delkhofen: Ed. Delkhofen. ISBN 978-3-936413-24-3.
• W. Kimmerle, M. Stroppel, Analysis für Ingenieure, Mathematiker und Physiker, Deilingen-Delkhofen: Ed. Delkhofen. ISBN 978-3-936413-23-6.
• J. Erven, M. Erven, J. Hörwick, Vorkurs Mathematik, Ein kompakter Leitfaden. München: Oldenbourg. ISBN 3-486-57629-1.
• W. Strampp, Elementare Mathematik, Vor- und Aufbaukurs. München: Oldenbourg. ISBN 3-486-25956-3.
• G. Bärwolff, Höhere Mathematik, für Naturwissenschaftler und Ingenieure. München: Spektrum (Elsevier). ISBN 3-8274-1436-9.
• N. Herrmann, Höhere Mathematik, für Ingenieure, Physiker und Mathematiker. München: Oldenbourg. ISBN 3-486-27498-8.
• J. Erven, D. Schwägerl, Mathematik für Ingenieure. München: Oldenbourg. ISBN 3-468-25954-7.
• K. Meyberg, P. Vachenauer, Höhere Mathematik 1. Differential- und Integralrechnung. Vektor- und Matrizenrechnung. Springer-Lehrbuch. Berlin: Springer.
• K. Burg, H. Haf, F. Wille, Höhere Mathematik für Ingenieure. Bd. 1: Analysis. Stuttgart: Teubner.
• K. Burg, H. Haf, F. Wille, Höhere Mathematik für Ingenieure. Bd. 2: Lineare Algebra. Stuttgart: Teubner.
• H. von Mangold, K. Knopp, Höhere Mathematik: eine Einführung für Studierende und zum Selbststudium. Stuttgart: S. Hirzel.
• V.I. Smirnov, Lehrgang der höheren Mathematik, Berlin: VEB Deutscher Verlag der Wissenschaften (ein Klassiker).
• I.N. Bronstein, K.A. Semendjajew, Taschenbuch der Mathematik, Frankfurt/Main: Verlag Harri Deutsch (als Formelsammlung).
• Mathematik Online: www.mathematik-online.org.