| ↰ 2.1 | Material | 2.8 → |
| ← 2.6 | HM 2 | 3.1 ↳ |
Wenn eine differenzierbare Funktion \( f\colon(a,b)\to\RR \) an der Stelle \( x_0^{}\in(a,b) \) ein lokales Extremum besitzt, dann gilt \( f'(x_0^{})=0 \).
Man möchte dieses notwendige Kriterium gerne umkehren, weil es leicht zu handhaben ist.
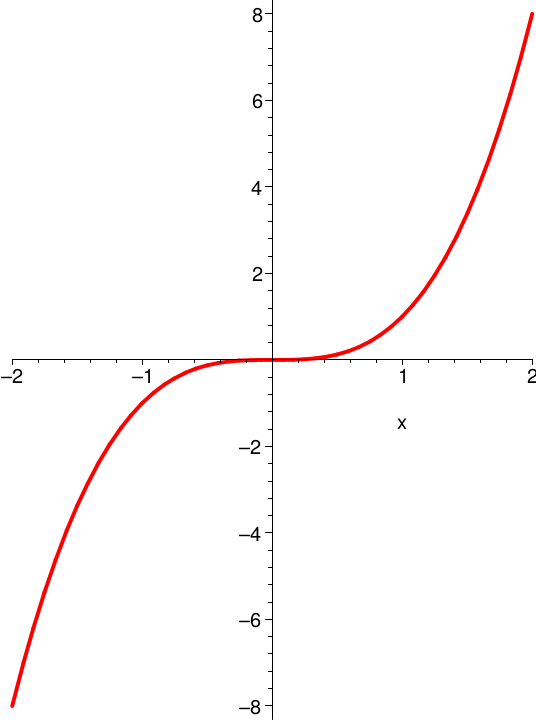
Allerdings zeigt \( f(x)=x^3 \), dass die simple Umkehrung des Kriteriums nicht gutgeht:
Bei \( x_0^{}=0 \) gilt \( f'(0)=0 \), aber es liegt kein lokales Extremum vor.

Es sei \( f\colon(a,b)\to\RR \) eine differenzierbare Funktion. Bei \( x_0^{}\in(a,b) \) gelte \( f'(x_0^{})=0 \).
Wenn die Ableitung bei \(x_0\) das Vorzeichen wechselt, liegt an der Stelle \(x_0\) ein lokales Extremum vor.
Genauer:
Wechselt das Vorzeichen von
\(
f'(x)
\)
von \(+\) (für \(x \lt x_0 \))
nach \(−\) (für \( x > x_0 \)), so besitzt \(f\) in \(x_0\) ein
lokales Maximum
[die Funktion steigt bis \(x_0\) , danach fällt sie].
Beim umgekehrten Vorzeichenwechsel liegt ein lokales Minimum vor.
Die Funktion \( f\colon\RR\to\RR\colon{}\pause x\mapsto x^3+b\,x^2+c\,x+d \) hat die Ableitung \( f'(x) = 3\,x^2+2\,b\,x+c \).
Die Nullstellen der Ableitung ergeben sich als
\(
x_0^{}=\frac13\left(-b-\sqrt{b^2-3\,c\,}\right)
\)
und
\(
x_1^{}=\frac13\left(-b+\sqrt{b^2-3\,c\,}\right)
\)
— wenn diese Stellen reelle Zahlen sind...
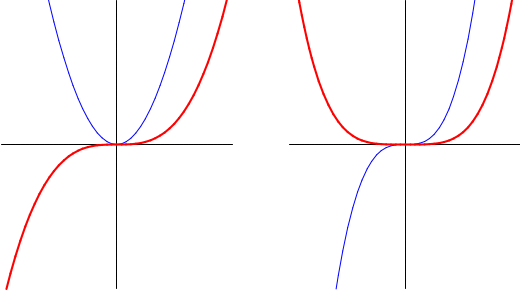
Für \( b^2 \gt 3\,c \) sind dies zwei reelle Nullstellen, die Ableitung hat zwischen diesen Nullstellen negatives, sonst positives Vorzeichen.
An beiden Stellen liegt also jeweils ein lokales Extremum vor:
bei \(x_0^{}\) ein lokales Maximum,
bei \(x_1^{}\) ein lokales Minimum.
Für \( b^2 = 3\,c \) fallen die beiden Nullstellen zusammen, der Vorzeichenwechsel verschwindet, und es liegt kein lokales Extremum vor.
Im Fall \( b^2 \lt 3\,c \) gibt es keine reellen Nullstellen der Ableitung und deswegen keine lokalen Extrema.
In der folgenden Skizze können Sie die Parameter \(b\), \(c\) und \(d\) selber
verändern.
Beachten Sie: die Skalierung der \(y\)-Achse ist so
angepasst, dass Sie möglichst viel vom Funktionsgraphen sehen.
Man kann den Vorzeichenwechsel oft am Verhalten der zweiten
Ableitung erkennen.
Dies ist Teil des folgenden, sehr allgemeinen
Kriteriums:
Es sei
\(
f\colon(a,b)\to\RR
\)
eine \(n\)-mal stetig differenzierbare Funktion,
und an der Stelle
\(
x_0^{}\in(a,b)
\)
gelte
\(
f'(x_0^{})=0
\)
\(
=f''(x_0^{})
\)
\(
=\cdots= f^{(n-1)}(x_0^{})
\),
aber
\(
f^{(n)}(x_0^{})\ne0
\).
(Die "Pünktchen-Schreibweise" kann
hier verwirren:
Für \(n=4\) verbirgt sich hinter den Pünktchen
gar nichts, für \(n=3\) fallen \(f''\) und \(f^{(n-1)}\) zusammen,
und für \(n=2\) bleibt nur die Bedingung \(f'(x_0)=0\) übrig.)
Nach dem Satz von Taylor 2.6.1 gilt
\( f(x) \) \( = \sum\limits_{k=0}^{n-1} \frac{f^{(k)}(x_0^{})}{k!} \, (x-x_0^{})^k \) \( + \frac{f^{(n)}\bigl(x_0^{}+\vartheta\,(x-x_0^{})\bigr)}{n!}\,(x-x_0^{})^{n} \) \( = f(x_0^{}) + 0 + \cdots + 0 \) \( + \frac{f^{(n)}\bigl(x_0^{}+\vartheta\,(x-x_0^{})\bigr)}{n!}\,(x-x_0^{})^{n} \)
mit \( \vartheta:=\vartheta_{x,x_0^{}}\in(0,1) \).
Ist \( f^{(n)}(x_0^{}) \gt 0 \), so gilt dies wegen der Stetigkeit von \( f^{(n)} \) für alle \(x\) aus einer geeigneten Umgebung \( U_\delta(x_0^{}) \).
Für \( x\in U_\delta(x_0^{}) \) liegt wegen \( \vartheta\in(0,1) \) auch \( x_0^{}+\vartheta(x-x_0^{}) \) in \( U_\delta(x_0^{}) \).
Falls \(n\) gerade ist, so gilt für \( x\in U_\delta(x_0^{}) \) stets \( \color{red}{(x-x_0^{})^n\ge0} \) und deswegen
\( f(x)-f(x_0^{}) \) \( = \frac{f^{(n)}\bigl(x_0^{}+\vartheta(x-x_0^{})\bigr)}{n!}\,(x-x_0^{})^n \) \( \ge 0 \).
Das bedeutet: An der Stelle \(x_0\) liegt ein lokales Minimum von \(f\) vor.
Analog schließt man im Fall \( \) für gerades \(n\) auf ein lokales Maximum.
Ist \(n\) ungerade, so wechselt der Faktor \( (x-x_0^{})^n \) bei \(x_0\) das Vorzeichen, aber das Vorzeichen von \( \frac{f^{(n)}\left(x_0^{}+\vartheta(x-x_0^{})\right)}{n!} \) bleibt:
Also liegt dann kein Extremum vor.
Sei \( f\colon(a,b)\to\RR \) differenzierbar, und es sei \( (x_0^{},f\color{red}{'}(x_0^{})) \) ein lokales Extremum der Ableitung \( f' \).
Dann heißt \( (x_0^{},f(x_0^{})) \) ein Wendepunkt von \(f\).
Zu Extrema und Wendepunkten gibt es ein interaktives Spielzeug hier und hier noch einmal (mit einer anderen Funktion).
| ↰ 2.1 | Material | 2.8 → |
| ← 2.6 | HM 2 | 3.1 ↳ |