| ↰ 3.1 | Material | 3.8 → |
| ← 3.6 | HM 2 | 4.1 ↳ |
Unsere Definition des Riemann-Integrals setzt mindestens voraus, dass die zu integrierende Funktion beschränkt und auch in den Randpunkten des Integrationsintervalls definiert ist.
Wir wollen die Frage der Existenz von Integralen diskutieren, bei denen diese Voraussetzungen nicht erfüllt sind.
Insbesondere sollen auch Integrationsintervalle der Form \( (a,b] \), \( [a,b) \) und \( (a,b) \) betrachtet werden.
Dabei kann man am offenen Ende des Intervalls auch \( a=-\infty \) oder \( b=+\infty \) zulassen.
Es sei \( -\infty \lt a \lt b\le+\infty \).
Die Funktion \( f\colon[a,b)\to\RR \) sei in jedem Teilintervall \( [a,\beta] \subset[a,b) \) integrierbar.
Dann heißt \(f\) uneigentlich integrierbar in \( [a,b) \), falls der Grenzwert
\( \ds \lim\limits_{\alert{\beta}\to b-0} \int\limits_a^{\alert{\beta}} f(x)\,\diff x \)
existiert (als reelle Zahl!).
Erinnerung: \(\lim\limits_{\alert{\beta}\to b-0}\)
bedeutet,
dass wir das Grenzverhalten untersuchen, wenn
\(\beta\) von links gegen \(b\) geht
— man könnte auch \(\lim\limits_{\alert{\beta}\nearrow b}\)
schreiben.
Man schreibt dann
\( \ds\int_a^b f(x)\,\diff x \) \( := \ds\int_a^{b-0} f(x)\,\diff x \) \( := \ds\lim\limits_{\beta\to b-0} \int_a^\beta f(x)\,\diff x \).
Analog definiert man für \( -\infty\le a \lt b \lt +\infty \):
\( \ds\int_a^b f(x)\,\diff x \) \( := \ds\int_{a+0}^{b} f(x)\,\diff x \) \( := \ds\lim\limits_{\alert{\alpha}\to a+0} \int_{\alert{\alpha}}^b f(x)\,\diff x \).
— man könnte auch \(\lim\limits_{\alert{\alpha}\searrow a}\)
schreiben.
Für \( -\infty\le a \lt b\le+\infty \) nennt man \( f\colon(a,b)\to\RR \) uneigentlich integrierbar in \( (a,b) \), falls es irgendein \( {\color{blue}{z}}\in(a,b) \) so gibt, dass die beiden uneigentlichen Integrale \( \int\limits_{a+0}^{\color{blue}{z}} f(x)\,\diff x \) und \( \int\limits_{\color{blue}{z}}^{b-0} f(x)\,\diff x \) existieren.
Man setzt dann
\( \ds \alert{\int\limits_a^b f(x)\,\diff x} \) \( := \ds \int\limits_{a+0}^{\color{blue}{z}} f(x)\,\diff x \) \( + \ds \int\limits_{\color{blue}{z}}^{b-0} f(x)\,\diff x \).
Unsere Voraussetzung, dass \(f\) auf allen Teilintervallen \( [\alpha,{\color{blue}{z}}]\subset(a,{\color{blue}{z}}] \) und \( [{\color{blue}{z}},\beta]\subset[{\color{blue}{z}},b) \) integrierbar ist, sichert die Unabhängigkeit dieser Definition von der Auswahl der Stelle \({\color{blue}{z}}\).
Das uneigentliche Integral
\(
\int\limits_0^{1-0} \frac1{\sqrt{1-x}} \,\diff x
\)
konvergiert:
Es gilt
\( \ds\int\limits_0^{1-0} \frac1{\sqrt{1-x}} \,\diff x \) \( = \ds\lim\limits_{\beta\to 1-0} \int\limits_0^\beta \frac1{\sqrt{1-x}} \,\diff x \) \( = \ds\lim_{\beta\to 1-0} \Bigl[-2\,\sqrt{1-x}\Bigr]_0^\beta \) \( = \ds\lim_{\beta\to 1-0} \Bigl(-2\,\sqrt{1-\beta} + 2\,\sqrt1\Bigr) \) \( = 2 \).
Die Funktion \( f\colon(0,1]\to\RR\colon{} x\mapsto\frac1x \) ist in \( (0,1] \) nicht uneigentlich integrierbar, denn es gilt:
\( \ds\lim\limits_{\alpha\to0+0} \int\limits_\alpha^1\frac1x \,\diff x \) \( = \lim\limits_{\alpha\to0+0} \Bigl[\ln |x|\Bigr]_\alpha^1 \) \( = \ln 1 - \lim\limits_{\alpha\to0+0} \ln\alpha \) \( = +\infty \).
Das uneigentliche Integral \( \int\limits_{-\infty}^{+\infty} |x|\,\E^{-x^2}\,\diff x \) konvergiert:
Um dies einzusehen, muss man \({\color{blue}{z}}\) wählen und die Konvergenz von \( \int\limits_{-\infty}^{{\color{blue}{z}}} |x|\,\E^{-x^2}\,\diff x \) und \( \int\limits_{{\color{blue}{z}}}^{+\infty} |x|\,\E^{-x^2}\,\diff x \) nachweisen.
Wir wählen \({\color{blue}{z}} = 0\) und erhalten
\( \int\limits_0^{+\infty} |x|\,\E^{-x^2}\,\diff x \) \( = \lim\limits_{\beta\to+\infty} \int\limits_0^{\beta} |x|\,\E^{-x^2}\,\diff x \) \( = \lim\limits_{\beta\to+\infty} \left[-\frac12\,\E^{-x^2}\right]_0^\beta \) \( = \lim\limits_{\beta\to+\infty} \frac12\left(-\E^{-\beta^2}+1\right) \) \( = \frac12 \,. \)
Aus Symmetriegründen liefert das linke uneigentliche Integral denselben Grenzwert, und wir erhalten
\( \int\limits_{-\infty}^{+\infty} |x|\,\E^{-x^2}\,\diff x \) \( = \int\limits_{-\infty}^{0} |x|\,\E^{-x^2}\,\diff x \) \( + \int\limits_{0}^{+\infty} |x|\,\E^{-x^2}\,\diff x \) \( = 1 \).

Die Funktion \( f\colon[a,b)\to\RR \) sei in jedem Teilintervall \( [a,\beta] \subset[a,b) \) integrierbar.
Es gelte \( 0\le f(x) \le g(x) \) für alle \( x\in[a,b) \).
Aus der Existenz von \( \int\limits_a^{b-0} g(x)\,\diff x \) folgt dann die Existenz von \( \int\limits_a^{b-0} f(x)\,\diff x \), und es gilt
\( \int\limits_a^{b-0} f(x)\,\diff x \le \int\limits_a^{b-0} g(x)\,\diff x \).
Jetzt sei \( f\colon[a,b)\to\RR \) beliebig.
Wenn \( \int\limits_a^ {b-0}\bigl|f(x)\bigr|\,\diff x \) existiert, nennt man das Integral absolut konvergent.
Man kann das Majoranten-Kriterium damit auch so zusammenfassen:
Die Funktion \( f\colon[a,b)\to\RR \) sei in jedem Teilintervall \( [a,\beta] \subset[a,b) \) integrierbar.
Gilt \( \bigl| f(x)\bigr|\le g(x) \) im Intervall \( [a,b) \) und existiert \( \int\limits_a^{b-0} g(x)\,\diff x \), so ist \( \int\limits_a^{b-0} f(x)\,\diff x \) absolut konvergent.
Das Majoranten-Kriterium für uneigentliche Integrale gilt völlig analog bezüglich eines links halboffenen Intervalls \( (a,b] \) bzw. eines offenen Intervalls \( (a,b) \), also für \( \int\limits_{a+0}^b f(x)\,\diff x \) bzw. \( \int\limits_{a+0}^{b-0} f(x)\,\diff x \).
Das uneigentliche Integral \( \int\limits_{\alert{1}}^{\alert{+\infty}} \frac1{x^\gamma}\,\diff x \) konvergiert genau dann, wenn \( \alert{\gamma \gt 1} \) ist.
Für \(\gamma\gt1\) gilt \( \lim\limits_{\beta\to+\infty}\left[\frac{1}{1-\gamma}\,x^{1-\gamma}\right]_1^\beta \) \( = \lim\limits_{\beta\to+\infty}\left(\frac{1}{1-\gamma}\,\left(\beta^{1-\gamma}-1\right)\right) \) \( = \frac{1}{\gamma-1} \).
Für \( \gamma=1 \) gilt \( \lim\limits_{\beta\to+\infty}\int_1^\beta \frac1x\,\diff x \) \( = \lim\limits_{\beta\to+\infty}\bigl(\ln\beta-\ln1\bigr) \) \( = +\infty \).
Für \( \gamma \lt 1 \) gilt \( \lim\limits_{\beta\to+\infty}\left[\frac{1}{1-\gamma}\,x^{1-\gamma}\right]_1^\beta \) \( = \lim\limits_{\beta\to+\infty}\left(\frac{1}{1-\gamma}\,\left(\beta^{1-\gamma}-1\right)\right) \) \( = +\infty \).
Für den letzten Fall \( \gamma \lt 1 \) wäre auch \( \int\limits_1^{+\infty} \frac1x\,\diff x \) als divergente Minorante brauchbar.
Das uneigentliche Integral \( \int\limits_{\alert{0+0}}^{\alert{1}} \frac1{x^\gamma}\,\diff x \) konvergiert genau dann, wenn \( \alert{\gamma<1} \) ist.
Man substituiert \( u=\frac1x \) in 3.7.8:
Mit \( \frac{\diff u}{\diff x}=-x^{-2} \) ergibt sich
\(\, \int\limits_\alpha^1 x^{-\gamma}\,\diff x \) \(\, = -\int\limits_{\alpha}^{1} x^{-\gamma+2}(-x^{-2})\,\diff x \) \(\, = -\int\limits_{x=\alpha}^{x=1} u(x)^{\gamma-2}\,\frac{\diff u}{\diff x}\,\diff x \) \( = -\int\limits_{u=1/\alpha}^{u=1/1} u^{\gamma-2}\,\diff u \) \( = \int\limits_{1}^{1/\alpha} \frac{1}{u^{2-\gamma}} \,\diff u \).
Nach 3.7.8 konvergiert unser uneigentliches Integral genau dann, wenn \( 2-\gamma \gt 1 \), also wenn \( \gamma \lt 1\) ist.
Die Beispiele 3.7.8 und 3.7.9 liefern oft brauchbare konvergente Majoranten bzw. divergente Minoranten.
Für alle \( x\in\RR \) gilt \( \frac{\cos x}{x^2+1} \) \( \le \frac{|\cos x|}{x^2+1} \) \( \le \frac1{x^2} \) und damit \( \left|\frac{\cos x}{x^2+1}\right| \le \frac1{x^2} \).
Das Integral \( \int\limits_1^{+\infty} \frac1{x^2}\,\diff x \) konvergiert nach 3.7.8 (wir setzen \(\gamma=2\)).
Nach dem Majoranten-Kriterium 3.7.5.3 konvergiert auch das Integral \( \int\limits_1^{+\infty} \frac{\cos x}{x^2+1}\,\diff x \) (sogar absolut).
Die Funktionen \(f\) und \(g\) seien im Intervall \( [a,b) \) stetig und positiv, außerdem gelte
\( \lim\limits_{x\to b-0}\frac{f(x)}{g(x)} = C \alert{\in\RR} \).
Im Fall \( C \gt 0 \) haben \( \int\limits_a^{b-0} f(x)\,\diff x \) und \( \int\limits_a^{b-0} g(x)\,\diff x \) das gleiche Konvergenzverhalten
(aber evtl. verschiedene Grenzwerte).
Im Fall \( C=0 \) folgt aus der Konvergenz von \( \int\limits_a^{b-0} g(x)\,\diff x \) die Konvergenz von \( \int\limits_a^{b-0} f(x)\,\diff x \).
Diese Aussagen gelten analog für links halboffene Intervalle.
Sei zuerst \( C \gt 0 \), dann gibt es zu \( \epsilon:=\frac C2 \) ein \( k\in[a,b) \) mit \( \forall\,x\in[k,b) \colon{} \) \( C-\epsilon \lt \frac{f(x)}{g(x)} \) \( \lt C+\epsilon \).
Folglich gilt
\( \forall\,x\in[k,b) \colon{} \) \( \frac C2\,g(x) \lt f(x) \) \( \lt \frac{3\,C}2\,g(x) \).
Das Majoranten-Kriterium 3.7.5 liefert nun
\( \int\limits_k^{b-0} f(x)\,\diff x \text{ konvergent} \) \( \implies \frac C2\,\int\limits_k^{b-0} g(x)\,\diff x \text{ konvergent} \) \( \implies \int\limits_k^{b-0} g(x)\,\diff x \text{ konvergent} \) \( \implies \frac{3\,C}2\,\int\limits_k^{b-0} g(x)\,\diff x \text{ konvergent} \) \( \implies \int\limits_k^{b-0} f(x)\,\diff x \text{ konvergent.} \)
Also konvergiert das Integral über \(f\) genau dann, wenn das Integral über \(g\) konvergiert.
Jetzt betrachten wir den Fall \(C = 0\).
Zu \( \epsilon:=1 \) finden wir \( k\in[a,b) \) mit
\( \forall\,x\in[k,b) \colon{} \) \( \frac{f(x)}{g(x)} \lt 1 \);
also \( f(x) \lt g(x) \).
Aus dem Majoranten-Kriterium 3.7.5 folgt nun
\( \int\limits_k^{b-0} g(x)\,\diff x \text{ konvergent} \) \( \implies \int\limits_k^{b-0} f(x)\,\diff x \text{ konvergent.} \)
Unsere Stetigkeitsvoraussetzung sichert die Existenz von \( \int\limits_a^k g(x)\,\diff x \) und \( \int\limits_a^k f(x)\,\diff x \).
Damit folgt die Behauptung.
Das Integral \( \int\limits_{0+0}^{+\infty} \E^{-t}\,t^{\alpha-1}\,\diff t \) konvergiert genau dann, wenn \(\alpha\gt 0\) gilt.
Man zerlegt das Integral in \( I_1 := \int\limits_{0+0}^{1} \E^{-t}\,t^{\alpha-1}\,\diff t \) und \( I_2 := \int\limits_{1}^{+\infty} \E^{-t}\,t^{\alpha-1}\,\diff t \)
und benutzt
\( \lim\limits_{t\to 0+0}\frac{\E^{-t}\,t^{\alpha-1}}{t^{\alpha-1}} \) \( = \lim\limits_{t\to 0+0} \E^{-t} \) \( = 1 \).
Das Grenzwertkriterium 3.7.11 sagt, dass \( I_1 \) und \( \int\limits_{0+0}^1 t^{\alpha-1}\,\diff t \) das gleiche Konvergenzverhalten haben.
Nach 3.7.9 existiert also \( I_1 \) genau dann, wenn \( \alpha \gt 0 \).
Das Integral \( I_2 \) konvergiert für jedes \( \alpha\in\RR \):
Für \( N\in\NN \) mit \( N\ge\alpha+1 \) liefert 2.5.6:
\( 0\le\lim\limits_{t\to+\infty} \frac{\E^{-t}\,t^{\alpha-1}}{t^{-2}} \) \( = \lim\limits_{t\to+\infty} \frac{\E^{-t}\,t^{\alpha+1}}{1} \) \( = \lim\limits_{t\to+\infty} \frac{t^{\alpha+1}}{\E^{t}} \) \( \le \lim\limits_{t\to+\infty} \frac{t^N}{\E^t} \) \( = 0 \).
Das Grenzwertkriterium und 3.7.8 liefern die Konvergenz.

|

|
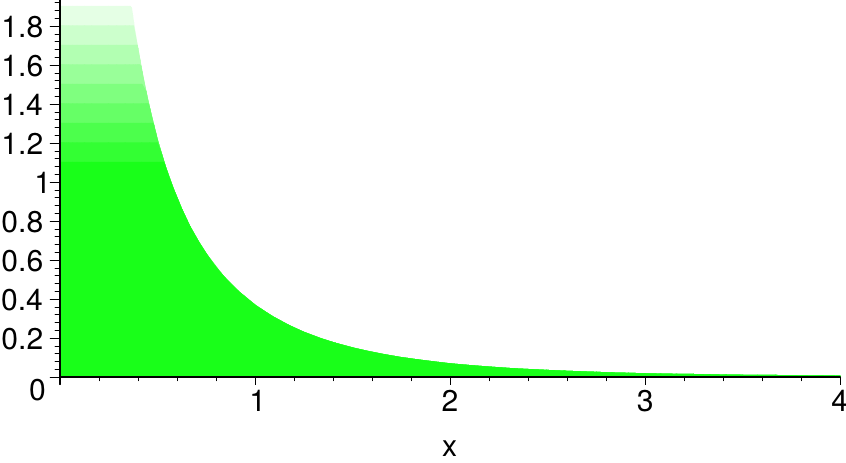
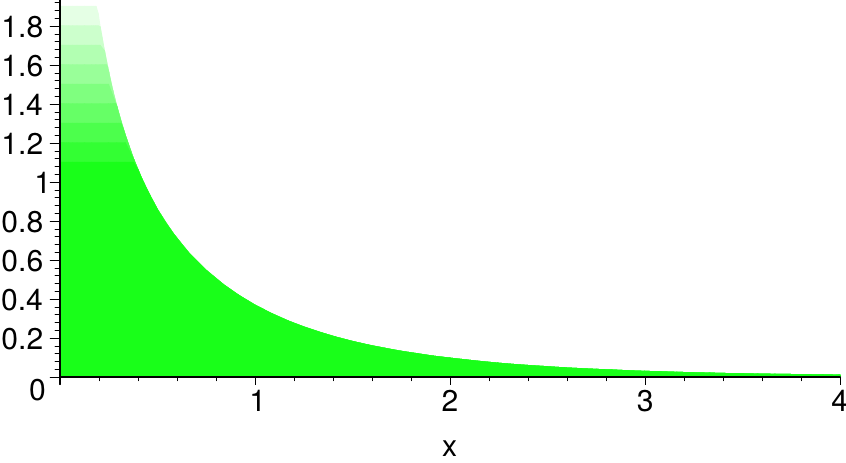
| \( \alpha=0 \) | \( \alpha=\frac12 \) |
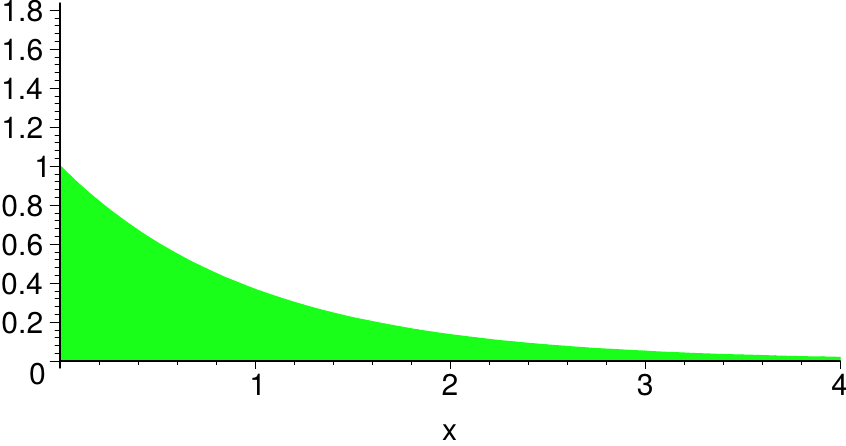
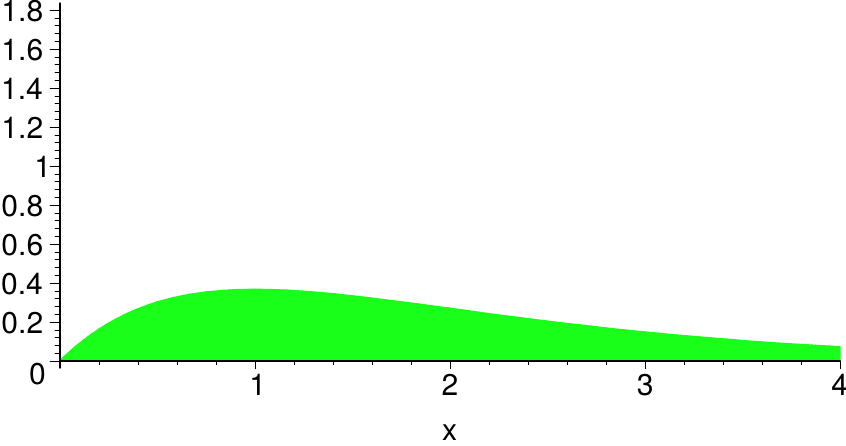
Obwohl die Graphen für \( \alpha=0 \) und \( \alpha=\frac12 \) recht ähnlich aussehen, ist das Konvergenzverhalten der uneigentlichen Integrale verschieden.
|
|
| \( \alpha=1 \) | \( \alpha=2 \) |
Für \( \alpha \gt 0 \) ist nach 3.7.12 durch
\( \ds \Gamma(\alpha):=\int_{0+0}^{+\infty} \E^{-t}\,t^{\alpha-1}\,\diff t \)
eine reelle Zahl definiert, wir erhalten damit eine Funktion
\( \Gamma\colon(0,+\infty)\to\RR\colon x\mapsto\Gamma(x) \).
Diese Gamma-Funktion ist eine (leicht verschobene) Fortsetzung der Fakultät:
Es gilt
\( \forall\,n\in\NN_0 \) \( \Gamma(n+1)=n! \)
Allgemein erfüllt die \(\Gamma\)-Funktion die Funktionalgleichung
\( \forall\,x\in(0,+\infty) \) \( \Gamma(x+1)=x\,\Gamma(x) \).
[Das sieht man durch partielle Integration.]
| ↰ 3.1 | Material | 3.8 → |
| ← 3.6 | HM 2 | 4.1 ↳ |