| ↰ 4.1 | Material | 4.6 → |
| ← 4.4 | HM 2 | 5.1 ↳ |
Wie im eindimensionalen Fall verstehen wir unter einer lokalen Extremalstelle einer Funktion \(f\) eine Stelle \(x_0\), an der \(f\) ein lokales Extremum hat:
Es muss also eine Umgebung \(U\) von \(x_0\) so geben, dass für \( x\in U\cap D \)
stets \( f(x)\ge f(x_0^{}) \) (lokales Minimum) oder aber
stets \( f(x)\le f(x_0^{}) \) gilt (lokales Maximum).
Kann man \(U = D\) wählen, so nennt man das Extremum wieder global (oder absolut).
Wir verallgemeinern zunächst das notwendige Kriterium der waagrechten Tangenten:
Es sei \( D\subseteq\RR^n \) offen, und es sei \( f\in\Cf1D \).
Wenn der Punkt \( x_0^{}\in D \) eine Extremalstelle von \(f\) ist, dann gilt jedenfalls \( \alert{\grad f(x_0^{})=0} \).
Jede Stelle \(x_0 \in D\) mit \( \grad f(x_0^{})=0 \) heißt kritische Stelle von \(f\), den Punkt \( \bigl(x_0^{},f(x_0^{})\bigr)\transp \) auf dem Graphen von \(f\) nennt man dann kritischen Punkt von \(f\).
Die waagrechte Tangential(hyper)ebene ist ein notwendiges, aber nicht hinreichendes Kriterium für die Existenz eines Extremums:
Nicht jede kritische Stelle ist Extremalstelle!
Mit Hilfe der Hesse-Matrix ergeben sich hinreichende Bedingungen für Extrema. Diese Bedingungen verallgemeinern die Betrachtung der zweiten Ableitung im eindimensionalen Fall.
Die Hesse-Matrix ist symmetrisch, und beschreibt eine quadratische Form. Die folgenden Begriffe werden benötigt:
Es sei \( A\in\RR^{n\times n} \) eine symmetrische Matrix.
Die zugehörige quadratische Form ist \( q_A^{}\colon \RR^n\to\RR\colon{} \) \( x\mapsto x\transp A\,x \).
Die Form \( q_A \) heißt
Man beachte, dass diese Fälle nicht alle Möglichkeiten abdecken:
Die Matrizen \( S:=\left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right) \) bzw. \( T:=\left( \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array}\right) \) beschreiben Formen \( q_S \) bzw. \( q_T \), die zwar nie negative Werte annehmen, aber trotzdem nicht positiv definit sind.
Konkret:
Wegen
\(
q_S\binom xy =
\left(
\begin{array}{cc}
x & y \\
\end{array}\right)
\left(
\begin{array}{cc}
1 & 0 \\
0 & 0
\end{array}\right)
\left(
\begin{array}{c}
x \\
y
\end{array}\right)
\)
\(
{} = x^2
\)
wird \(q_S\binom xy\) zwar nie negativ (für \(x,y\in\RR\)),
aber es gilt z.B. \(q_S\binom01=0\), obwohl \(\binom01 \ne \binom00\).
Analog gilt
\(
q_T\binom xy =
\left(
\begin{array}{cc}
x & y \\
\end{array}\right)
\left(
\begin{array}{cc}
1 & 1 \\
1 & 1
\end{array}\right)
\left(
\begin{array}{c}
x \\
y
\end{array}\right)
\)
\(
{} = x^2+xy+yx+y^2 = (x+y)^2 \ge 0
\),
aber \(q_T\binom{1}{-1} = 0 \).
Jede reelle symmetrische Matrix A lässt sich nach einem Resultat aus der linearen Algebra orthogonal diagonalisieren:
Es gibt also eine quadratische Matrix \(F\) so, dass \(F\transp F\) die Einheitsmatrix und \(F\transp A\, F\) eine Diagonalmatrix ist.
Die Diagonaleinträge \( \lambda_1,\ldots,\lambda_n \) von \(F\transp A\, F\) sind dann gerade die Eigenwerte von \(A\).
Wegen \( q_A^{}(F\,x) = q_{F\transp A\,F}(x) \) \( = \lambda_1 x_1^2+\cdots\lambda_n x_n^2 \) erhalten wir:
Die Form \(q_A\) ist
Noch einmal der Hinweis: diese drei Sonderfälle decken nicht alle
denkbaren Möglichkeiten ab!
Die oben betrachteten Formen \(q_S\) und \(q_T\) fallen
unter keinen der drei Fälle:
Die Matrizen \(S\) und \(T\) haben die Eigenwerte \(0\) und \(1\)
bzw. \(0\) und \(2\).
Die abgedeckten Fälle sind aber gerade die, in denen das folgende Kriterium hilft:
Es sei \( D\subseteq\RR^n \) offen, es sei \( f\in\Cf2D \) und es sei \(a\in D\) eine kritische Stelle.
Dann gilt:
Kritische Punkte, an denen keine lokalen Extrema vorliegen, heißen Sattelpunkte.
Kritische Punkte mit indefiniter Hesse-Matrix sind jedenfalls Sattelpunkte.
In den Fällen, in denen die Hesse-Matrix weder positiv noch negativ definit und auch nicht indefinit ist, kann man mit 4.5.5 keine Entscheidung fällen.
Wir betrachten das Definitheitskriterium 4.5.5 speziell für den Fall einer Funktion \(f\in\Cf2D\) in zwei Veränderlichen:
\( f\colon D\to\RR \colon{}\pause \binom xy \mapsto f\binom xy \) mit \( D\subseteq\RR^2 \).
Die Hesse-Matrix ist dann \( \Hesse fa \pause = \left( \begin{array}{cc} f_{xx}(a) & f_{xy}(a) \\ f_{xy}(a) & f_{yy}(a) \end{array} \right) \).
Es sei \( a\in \inn{D} \) eine kritische Stelle, und es seien \( \lambda_1 \) und \( \lambda_2 \) die beiden Eigenwerte von \( \Hesse fa \).
Wir wissen aus der linearen Algebra:
\( \lambda_1+\lambda_2 = \trace(\Hesse fa) \) und \( \lambda_1\lambda_2 = \det(\Hesse fa) \).
Man kann diese beiden Relationen auch schnell durch Vergleich der Koeffizienten im charakterstischen Polynom \( \det(\Hesse fa-\lambda\,\En2) \) \( = (\lambda-\lambda_1)(\lambda-\lambda_2) \) verifizieren.
Der Eigenwert \(0\) tritt genau dann auf, wenn die Determinante \(0\) ist:
\( 0\in\{\lambda_1,\lambda_2\} \) \( \iff \color{blue}{\det(\Hesse fa)=0} \).
In diesem Fall erlaubt die Hesse-Matrix keine Entscheidung über den Typ der kritischen Stelle \(a\).
Im Fall \( \color{gren}{\det(\Hesse fa) \lt 0} \) haben die beiden Eigenwerte verschiedenes Vorzeichen, damit beschreibt die Hesse-Matrix eine indefinite quadratische Form und es liegt bei \(a\) ein Sattelpunkt vor.
Es bleibt der Fall \( \color{red}{\det(\Hesse fa) \gt 0} \).
Jetzt haben die beiden Eigenwerte gleiches Vorzeichen, und dieses ist auch das Vorzeichen von \( \trace(\Hesse fa) = \lambda_1+\lambda_2 \).
Es liegt also im Fall positiver Determinante genau dann ein lokales Maximum vor, wenn die Spur von \( \Hesse fa \) negativ ist;
ein lokales Minimum liegt genau dann vor, wenn diese Spur positiv ist.
Es sei \( D\subseteq\RR^2 \) offen, \( f\in\Cf2D \), und es sei \( a\in D \) eine kritische Stelle (d. h. \( \grad f(a)=0 \)).
Dann gilt:
Im Fall \( \color{blue}{\det(\Hesse fa)=0} \) kann man mit der Hesse-Matrix allein keine Entscheidung fällen.
Es ist tatsächlich so, dass bei positiver Determinante der Hesse-Matrix \( \Hesse fa \) auch die beiden Diagonaleinträge stets dasselbe Vorzeichen haben — man kann also das Vorzeichen der Spur (und damit der Eigenwerte) schon an einem einzigen Diagonaleintrag direkt ablesen:
Für \( \color{red}{f_{xx}(a) \gt 0} \) liegt ein lokales Minimum,für \( \color{red}{f_{xx}(a) \lt 0} \) liegt ein lokales Maximum vor.
Dies ist ein Spezialfall eines allgemeinen Satzes:
Man kann die positive Definitheit einer reellen symmetrischen Matrix
beliebiger Größe allein an der Positivität der so genannten
Hauptminoren ablesen.
Die Funktion \( f\colon \RR^2 \to \RR \colon \) \( \binom xy \mapsto x^2+y^2+x \) ist beliebig oft stetig partiell differenzierbar.
Notwendiges Kriterium für ein lokales Extremum in \( a=\binom xy \) ist
\( \left( \begin{array}{c} 0 \\ 0 \end{array} \right) = \grad f(a) \) \( = \left( \begin{array}{c} 2\,x+1 \\ 2\,y \end{array} \right) \),
dies ist genau für \( a=\binom{-1/2}0 \) erfüllt.
Mit \( f_{xx}(a)=2 = f_{yy}(a) \) und \( f_{xy}(a)=0 \) erhalten wir
\( \Hesso f\binom{-1/2}0 = \left( \begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array}\right) \).
Die Hesse-Matrix ist positiv definit, es liegt in \( \binom{-1/2}0 \) also ein lokales Minimum \( \left(\left(-\frac12,0\right),-\frac14\right)\transp \) vor.
Dieses Minimum ist sogar global:
Wegen \( x^2+x+\frac14 + y^2 \) \( = \left(x+\frac12\right)^2 + y^2 \) \( \ge0 \) gilt \( f\binom xy = \) \( x^2+y^2+x \) \( \ge -s\frac14 \) \( = f\binom{-1/2}0 \) für alle \( \binom xy\in\RR^2 \).
Die Funktion
\( f\colon \RR^2\to\RR\colon \) \( \binom xy\mapsto x\,y\,(1-x^2-y^2) \)
ist ebenfalls auf ganz \( \RR^2 \) beliebig oft stetig partiell differenzierbar.
Die kritischen Stellen ergeben sich aus der Bedingung
\( \left( \begin{array}{c} 0 \\ 0 \end{array}\right) \) \( = \grad f\binom xy \) \( = \left( \begin{array}{c} y-3\,x^2\,y-y^3 \\ x-x^3-3\,x\,y^2 \end{array}\right) \) \( = \left( \begin{array}{c} y\,(1-3\,x^2-y^2) \\\pause x\,(1-x^2-3\,y^2) \end{array}\right) \).
Mit Hilfe von Fallunterscheidungen (je nachdem, ob \(x\) oder \(y\) gleich Null sind oder nicht), findet man die neun kritischen Stellen
\( P_1=\ds\binom{1}{0} \), \( P_2=\ds\binom{-1}{0} \), \( P_3=\ds\binom{0}{0} \),
\( P_4=\ds\binom{0}{1} \), \( P_5=\ds\binom{0}{-1} \),
\( P_6=\ds\binom{1/2}{1/2} \), \( P_7=\ds\binom{1/2}{-1/2} \), \( P_8=\ds\binom{-1/2}{1/2} \), \( P_9=\ds\binom{-1/2}{-1/2} \).
Mit
\( f_{xx}\binom uv=-6\,u\,v \)
\( f_{xy}\binom uv=1-3\,u^2-3\,v^2 \)
\( f_{yy}\binom uv=-6\,u\,v \)
ergibt sich als Hesse-Matrix
\( \Hesso f\binom uv = \) \( \left( \begin{array}{cc} -6uv & 1-3(u^2+v^2) \\ 1-3(u^2+v^2) & -6uv \end{array}\right) \),
mit Determinante \( d\binom uv = \) \( 36\,u^2\,v^2 - \bigl(1-3\,u^2-3\,v^2\bigr)^2 \).
Für \( P_1,\ldots,P_5 \) gilt \( \color{green}{d(P_j)<0} \).
Also liegen an diesen Stellen Sattelpunkte vor.
Für \( P_6,\ldots,P_9 \) gilt dagegen \( \color{red}{d(P_j)=2>0} \).
Wir berechnen
\( f_{xx}\left(P_6\right) \) \( = f_{xx}\binom {1/2}{1/2} \) \( = -\frac64 \) \( = f_{xx}\binom {-1/2}{-1/2} \) \( = f_{xx}\left(P_9\right) \)
und
\( f_{xx}\left(P_7\right) \) \( = f_{xx}\binom {1/2}{-1/2} \) \( = \frac64 \) \( = f_{xx}\binom {-1/2}{1/2} \) \( = f_{xx}\left(P_8\right) \).
Demnach sind \( (P_6,f(P_6)) \) und \( (P_9,f(P_9)) \) lokale Maxima, dagegen liegen bei \( P_7 \) und \( P_8 \) lokale Minima vor.
Den Typ der kritischen Stellen in 4.5.11 hätte man auch durch eine Diskussion des Vorzeichens der Funktionswerte bestimmen können.
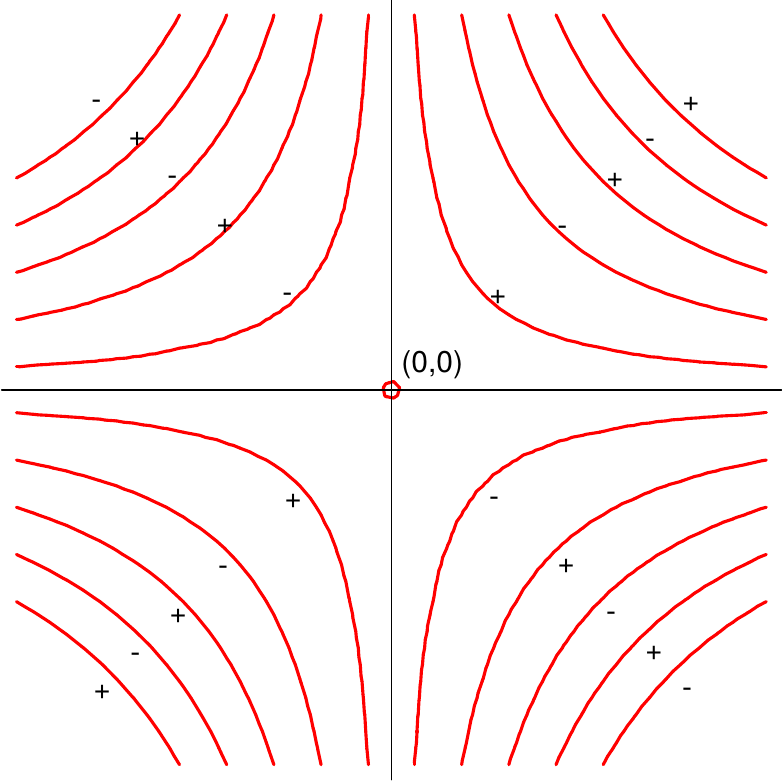
Die blauen Linien bilden die Niveaumenge zum Niveau \(0\); die beiden Ellipsen sind die Nullstellenmengen der „interessanten“ Faktoren in \( f_x \) bzw \( f_y \).
Das Vorzeichen von \( f\binom xy=x\,y\,(1-x^2-y^2) \) ergibt sich aus den Vorzeichen der drei Faktoren (in der Skizze angedeutet durch „ + + + “ etc.)
Die Funktion \( f\colon\RR^2\to\RR\colon \) \( \binom xy\mapsto\sin(x\,y) \) hat den Gradienten \( \grad f\binom xy \) \( = \left( \begin{array}{c} y\,\cos(x\,y) \\ x\,\cos(x\,y) \end{array}\right) \), als kritische Stellen erhalten wir neben dem Ursprung \(\binom00\) alle Punkte der Form
\( \binom xy \) mit \( \cos(x\,y)=0 \):
also \( \binom xy \) mit \( x\,y\in\frac\pi2+\pi\,\ZZ \).
Diese Punkte liegen auf Hyperbelästen, deren Asymptoten die Koordinatenachsen sind.
Die Hesse-Matrix \( \Hesso f\binom xy = \) \( \left( \begin{array}{cc} f_{xx}\binom xy & f_{xy}\binom xy \\ f_{yx}\binom xy & f_{yy}\binom xy \end{array}\right) \) hat die Einträge
\( f_{xx}\binom xy = -y^2\sin(xy) \),
\( f_{xy}\binom xy \) \( = -xy\sin(xy)+\cos(xy) \) \( = f_{yx}\binom xy \),
\( f_{yy}\binom xy = -x^2\sin(xy) \) und die Determinante
\( \det\left(\Hesso f\binom xy\right) \) \( = x^2 y^2 \sin(x y)^2 \) \( - \left(-x y \sin(x y)+\cos(x y)\right)^2 \)
\( = x^2 y^2 \sin(x y)^2 \) \( -x^2 y^2 \sin(x y)^2 \) \( + 2 x y \sin(x y) \cos(x y) \) \( -\cos(x y)^2 \) \( = \left(2 x y \sin(x y)-\cos(x y)\right) \cos(x y) \).
Für den Ursprung ergibt sich \( \det\left( \Hesso f\binom 00\right) \) \( = -\cos(0)^2 \) \( = -1 \color{green}{\lt0} \), dort liegt also ein Sattelpunkt vor.
An allen anderen kritischen Stellen \(b\) gilt \( \color{blue}{\det\left(\Hesse f{b}\right)=0} \), unser Kriterium 4.5.8 liefert also keine Aussage.
Man sieht in diesem Fall aber leicht:
Die Hyperbeläste, die von den kritischen Stellen gebildet werden,
gehören jeweils zu Niveaulinien zu den Niveaus \(+1\) bzw. \(−1\).
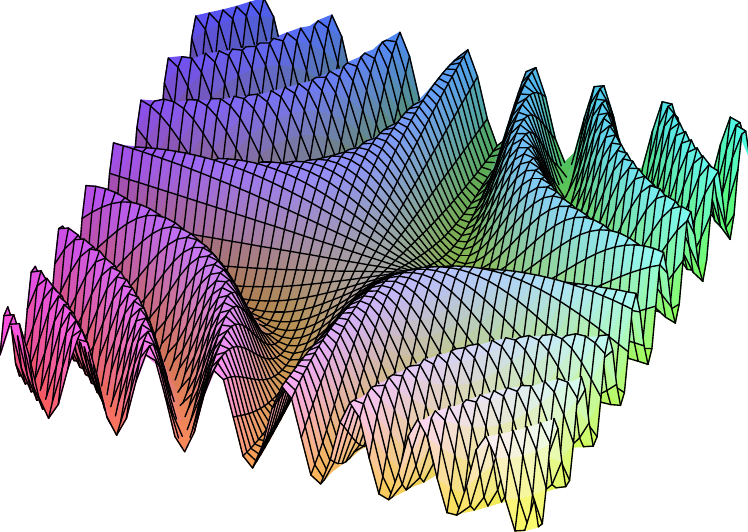
Wenn Sie mit der Maus über das Bild fahren, wird das Niveau \(+1\) angedeutet.
Die Funktion nimmt auf diesen Niveaus (globale) Maxima und Minima an!
Bei der Suche nach Extrema haben wir uns bisher beschränkt auf Stellen im Inneren des Definitionsbereichs (oft implizit durch die Annahme, dass der Definitionsbereich offen sei).
Nur unter dieser Annahme (neben der Differenzierbarkeit) ist es richtig, dass die Extrema an Stellen mit horizontaler Tangentialhyperebene (also bei kritischen Stellen) zu finden sind. Wenn der Definitionsbereich neben inneren Punkten auch Randpunkte enthält (oder gar nur aus solchen besteht) muss man diese gesondert untersuchen!
Die Funktion \( f\colon[0,1]\to\RR\colon \) \( t\mapsto\cos(t) \) hat ein Maximum bei \(t = 0\) (mit zufällig horizontaler Tangente) und ein Minimum bei \(t = 1\) (an diesem Randpunkt ist die Tangente nicht horizontal).
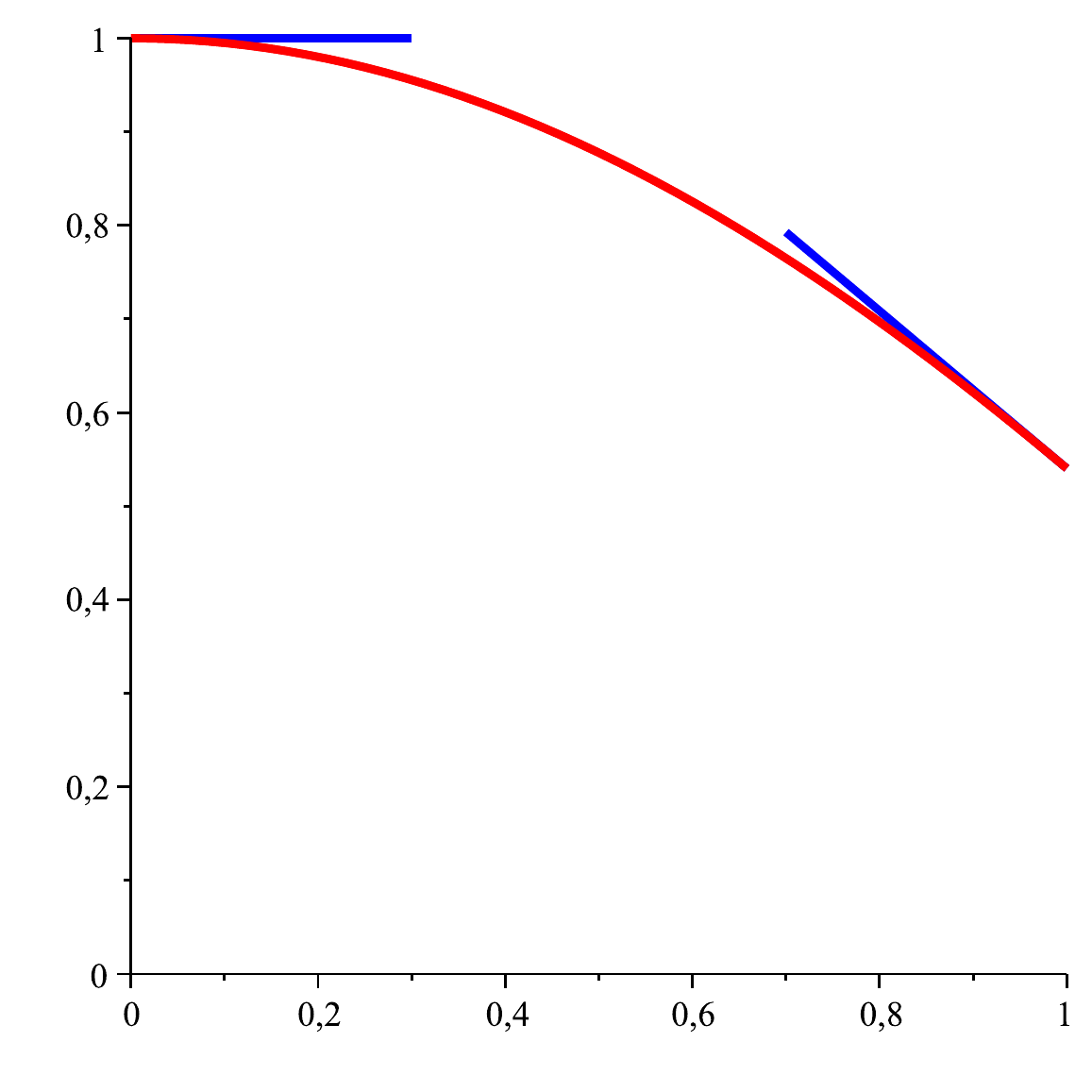
Die Funktion \( g\colon D:=[-1,1]^2 \to\RR\colon \) \( \left( \begin{smallmatrix} x \\ y \end{smallmatrix} \right) \mapsto x^2+y^2 \) hat ein Minimum bei \( \binom00 \):
Das ist ein innerer Punkt von \(D\); die Tangentialebene liegt horizontal.
Die Maxima liegen auf dem Rand; die Tangentialebenen sind dort nicht horizontal.
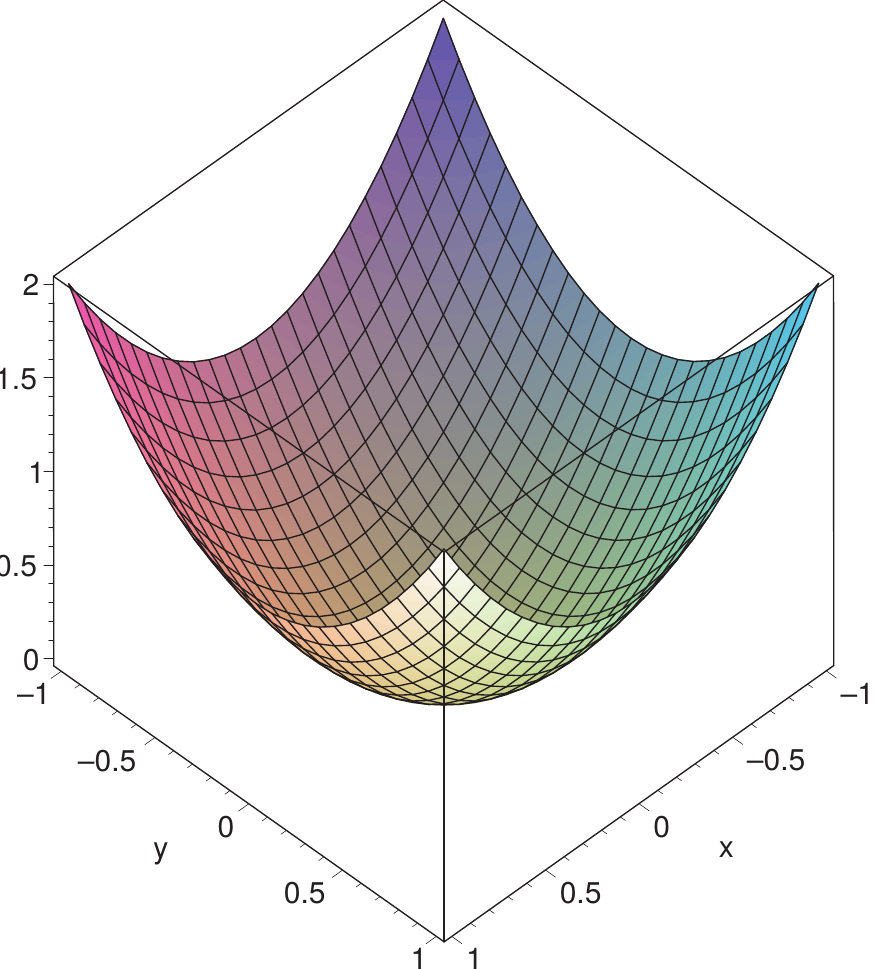
Wenn der Rand des Definitionsbereichs geeignet ist, kann man die Suche nach Extrema auf dem Rand mit den Methoden des nächsten Abschnitts betreiben.
| ↰ 4.1 | Material | 4.6 → |
| ← 4.4 | HM 2 | 5.1 ↳ |