| ↰ 4.1 | Material | 4.6 → |
| ← 4.4 | HM 2 | 5.1 ↳ |
Wie im eindimensionalen Fall verstehen wir unter einer lokalen
Extremalstelle einer Funktion
Es muss also eine Umgebung
stets
stets
Kann man
Wir verallgemeinern zunächst das notwendige Kriterium der waagrechten Tangenten:
Es sei
Wenn der Punkt
Jede Stelle
Die waagrechte Tangential(hyper)ebene ist ein notwendiges, aber nicht hinreichendes Kriterium für die Existenz eines Extremums:
Nicht jede kritische Stelle ist Extremalstelle!
Mit Hilfe der Hesse-Matrix ergeben sich hinreichende Bedingungen für Extrema. Diese Bedingungen verallgemeinern die Betrachtung der zweiten Ableitung im eindimensionalen Fall.
Die Hesse-Matrix ist symmetrisch, und beschreibt eine quadratische Form. Die folgenden Begriffe werden benötigt:
Es sei
Die zugehörige quadratische Form ist
Die Form
Man beachte, dass diese Fälle nicht alle Möglichkeiten abdecken:
Die Matrizen
Konkret:
Wegen
aber es gilt z.B.
Analog gilt
aber
Jede reelle symmetrische Matrix A lässt sich nach einem Resultat aus der linearen Algebra orthogonal diagonalisieren:
Es gibt also eine quadratische Matrix
Die Diagonaleinträge
Wegen
Die Form
Noch einmal der Hinweis: diese drei Sonderfälle decken nicht alle
denkbaren Möglichkeiten ab!
Die oben betrachteten Formen
Die abgedeckten Fälle sind aber gerade die, in denen das folgende Kriterium hilft:
Es sei
Dann gilt:
Kritische Punkte, an denen keine lokalen Extrema vorliegen, heißen Sattelpunkte.
Kritische Punkte mit indefiniter Hesse-Matrix sind jedenfalls Sattelpunkte.
In den Fällen, in denen die Hesse-Matrix weder positiv noch negativ definit und auch nicht indefinit ist, kann man mit 4.5.5 keine Entscheidung fällen.
Wir betrachten das Definitheitskriterium 4.5.5
speziell für den Fall einer Funktion
Die Hesse-Matrix ist dann
Es sei
Wir wissen aus der linearen Algebra:
Man kann diese beiden Relationen auch schnell durch Vergleich
der Koeffizienten im charakterstischen Polynom
Der Eigenwert
In diesem Fall erlaubt die Hesse-Matrix keine Entscheidung über den
Typ der kritischen Stelle
Im Fall
Es bleibt der Fall
Jetzt haben die beiden Eigenwerte gleiches Vorzeichen, und dieses ist
auch das Vorzeichen von
Es liegt also im Fall positiver Determinante genau dann
ein lokales Maximum vor, wenn die Spur von
ein lokales Minimum liegt genau dann vor, wenn diese Spur positiv ist.
Es sei
Dann gilt:
Im Fall
Es ist tatsächlich so, dass bei positiver Determinante der Hesse-Matrix
Für
Dies ist ein Spezialfall eines allgemeinen Satzes:
Man kann die positive Definitheit einer reellen symmetrischen Matrix
beliebiger Größe allein an der Positivität der so genannten
Hauptminoren ablesen.
Die Funktion
Notwendiges Kriterium für ein lokales Extremum in
dies ist genau für
Mit
Die Hesse-Matrix ist positiv definit, es liegt in
Dieses Minimum ist sogar global:
Wegen
Die Funktion
ist ebenfalls auf ganz
Die kritischen Stellen ergeben sich aus der Bedingung
Mit Hilfe von Fallunterscheidungen (je nachdem, ob
Mit
ergibt sich als Hesse-Matrix
mit Determinante
Für
Also liegen an diesen Stellen Sattelpunkte vor.
Für
Wir berechnen
und
Demnach sind
Den Typ der kritischen Stellen in 4.5.11 hätte man auch durch eine Diskussion des Vorzeichens der Funktionswerte bestimmen können.
Die blauen Linien bilden die Niveaumenge zum Niveau
Das Vorzeichen von
Die Funktion
also
Diese Punkte liegen auf Hyperbelästen, deren Asymptoten die Koordinatenachsen sind.
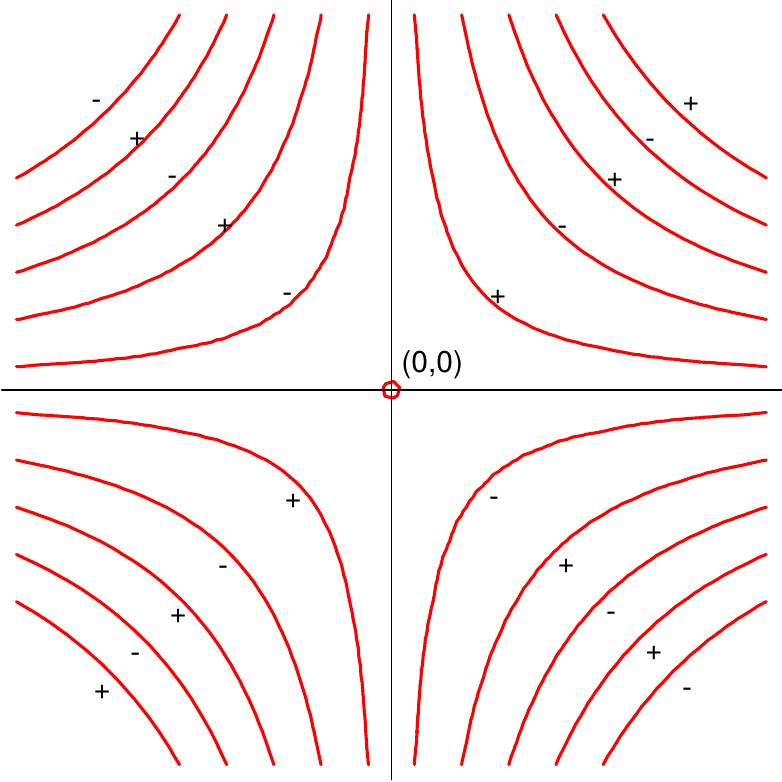
Die Hesse-Matrix
Für den Ursprung ergibt sich
An allen anderen kritischen Stellen
Man sieht in diesem Fall aber leicht:
Die Hyperbeläste, die von den kritischen Stellen gebildet werden,
gehören jeweils zu Niveaulinien zu den Niveaus
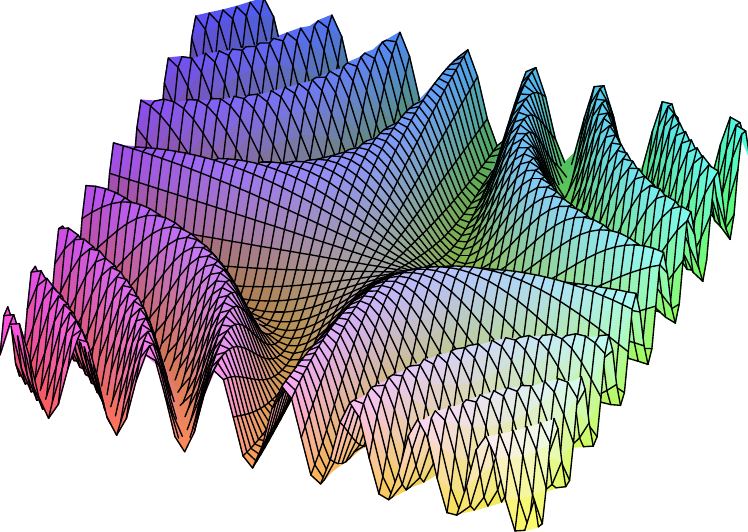
Wenn Sie mit der Maus über das Bild fahren, wird das Niveau
Die Funktion nimmt auf diesen Niveaus (globale) Maxima und Minima an!
Bei der Suche nach Extrema haben wir uns bisher beschränkt auf Stellen im Inneren des Definitionsbereichs (oft implizit durch die Annahme, dass der Definitionsbereich offen sei).
Nur unter dieser Annahme (neben der Differenzierbarkeit) ist es richtig, dass die Extrema an Stellen mit horizontaler Tangentialhyperebene (also bei kritischen Stellen) zu finden sind. Wenn der Definitionsbereich neben inneren Punkten auch Randpunkte enthält (oder gar nur aus solchen besteht) muss man diese gesondert untersuchen!
Die Funktion
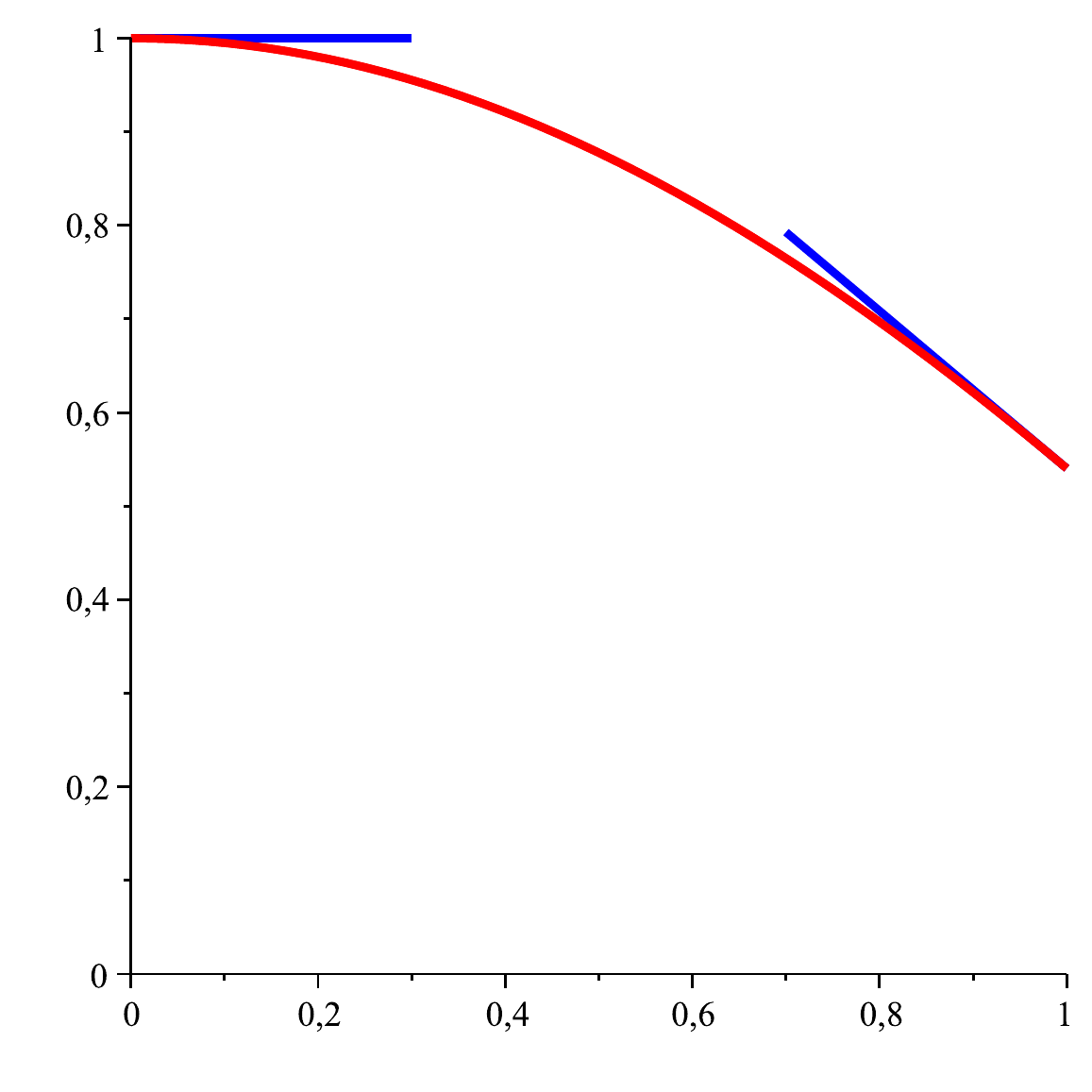
Die Funktion
Das ist ein innerer Punkt von
Die Maxima liegen auf dem Rand; die Tangentialebenen sind dort nicht horizontal.
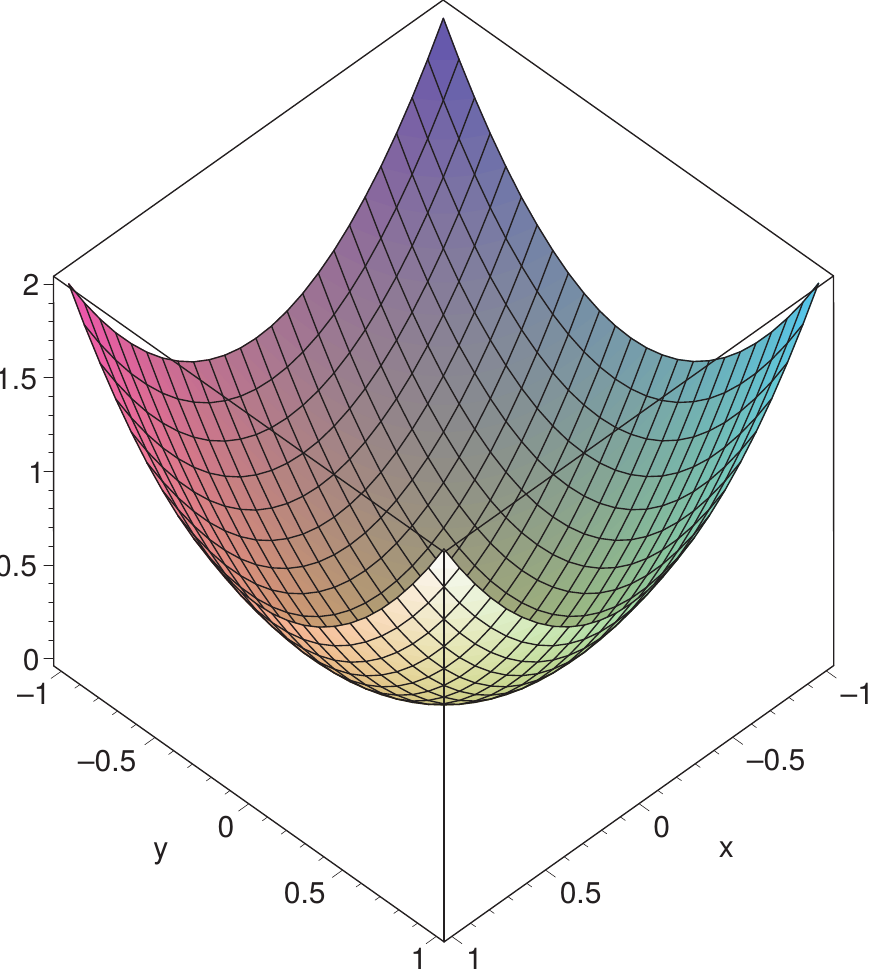
Wenn der Rand des Definitionsbereichs geeignet ist, kann man die Suche nach Extrema auf dem Rand mit den Methoden des nächsten Abschnitts betreiben.
| ↰ 4.1 | Material | 4.6 → |
| ← 4.4 | HM 2 | 5.1 ↳ |