| ↰ 4.1 | Material | |
| ← 4.8 | HM 2 | 5.1 ↳ |
Für \( D\subseteq\RR^n \) betrachten wir eine Funktion \( f\in\Cf1D \), eine Stelle \( a\in\inn D \) und einen Vektor \( v\in\RR^n \) mit Einheitslänge: \(\alert{|v | = 1}\).
Für die Richtungsableitung wissen wir aus 4.3.12: \( \partial_v^{} f(a) \) \( = \grad f(a)\skalp v \) \( = \vert\grad f(a)\vert\,\vert v\vert\,\cos\alpha \) \( = \vert\grad f(a)\vert\,\cos\alpha \),
wobei \( \alpha \) den Winkel zwischen den Vektoren \( \grad f(a) \) und \(v\) bezeichnet.
Der Wert der Richtungsableitung ist die Steigung der Tangente an den Graphen von \(f\) in Richtung \(v\).
Dieser Wert wird offenbar dann am größten, wenn \( \cos\alpha \) maximal wird
(also \( \cos\alpha=1 \): das geschieht bei \( \alpha=0 \)),
und am kleinsten, wenn \( \cos\alpha \) minimal wird
(also \( \cos\alpha=-1 \): bei \( \alpha=\pi \)).
Die Richtung von \( \grad f(a) \) ist die Richtung des steilsten Anstiegs von \(f\) an der Stelle \(a\).
Die umgekehrte Richtung (also die von \( - \grad f(a) \)) ist die der maximalen Abnahme der Funktion steilster Abstieg.
Es sei \( D=\inn D\subseteq\RR^n \) und \( f\in\Cf1D \).
Für jeden Wert \(k\) im Bild von \(f\) definiert die Gleichung \( f(x)=k \) eine Niveaumenge \( H := \set{x\in D}{f(x)=k} \) in \(D\).
Bis auf Ausartungsfälle ist diese Niveaumenge eine Hyperfläche.
Im Spezialfall \(n = 2\) erwarten wir eine Niveaulinie, für \(n = 3\) liegt im Allgemeinen eine Fläche in \( \RR^3 \) vor.
Wir nehmen im Folgenden an, dass \(H\) nicht zu isolierten Punkten ausgeartet ist.
Wir betrachten ein Intervall \(I\) und eine differenzierbare Abbildung \( C\colon I\to\RR^n \) mit \( C(I)\subseteq H \)
— also die Parametrisierung einer in \(H\) verlaufenden Kurve.
Eine tiefer gehende Diskussion des Begriffs "Kurve" nehmen wir später in 5.1.3 vor.
Wir nehmen außerdem an, dass für alle \(t\in I\) die Ableitung \(C'(t)\) vom Nullvektor verschieden ist (damit beschreibt \(C'(t)\) die Richtung der Tangente an die Kurve, vgl. 4.7.4).
Es gilt
\( \forall\,t\in I\colon \) \( f\bigl(C(t)\bigr) = k \).
Also ist die Funktion
\( f\circ C\colon I\to\RR \)
konstant, und es gilt
\( 0 = (f\circ C)'(t) \) \( = \Jac f{C(t)}\, C'(t) \) \( = \grad f\bigl(C(t)\bigr)\skalp C'(t) \)
nach der Kettenregel 4.8.3.
Für jeden Punkt \( a\in D \) und jede Kurve durch \(a\) in der Hyperfläche \( H=\set{x\in D}{f(x)=f(a)} \) steht \( \grad f(a) \) senkrecht zur Tangente an die Kurve im Punkt \(a\).
Wir betrachten einen Punkt \( a \in D \) mit \( {\grad f(a)\ne0} \).
Im Fall \(n = 2\) ist \( \grad f(a) \) senkrecht zur Richtung der Tangente in \( a=\binom{a_1^{}}{a_2^{}} \) an die Niveaulinie \( \bigset{x=\binom{x_1^{}}{x_2^{}}\in D}{\kern-.2em f(x)=f(a)\kern-.2em } \).
Diese Tangente hat also die Gleichung
\( \grad f(a)\skalp x = \grad f(a)\skalp a \),
bzw.
\( \grad f(a)\skalp (x-a) = 0 \).
Im Fall \(n = 3\) steht \( \grad f(a) \) senkrecht zur Tangentenrichtung jeder Kurve durch \( a = (a_1,a_2,a_3)\transp \) in
\( H = \) \( \bigset{x= \left(\begin{array}{c}x_1^{}\\x_2^{}\\x_3^{}\end{array}\right)\in D}{\kern-.2em f(x)=f(a)\kern-.2em } \).
Also steht \( \grad f(a) \) senkrecht zur Tangentialebene an \(H\) in \(a\).
Diese Tangentialebene hat also die Gleichung
\( \grad f(a)\skalp (x-a) = 0 \).
Die Gerade \(N\), die in \(a\) auf \(H\) senkrecht steht, hat die Parameterdarstellung
\( N\colon\ a+\mu\,\grad f(a) ,\ \mu\in\RR \).
Wir betrachten eine Quadrik \( Q=\bigset{x\in\RR^n}{f(x)=0} \), beschrieben als Nullstellenmenge einer Funktion \( f\colon\RR^n\to\RR \) (nämlich eines Polynoms \(f\) vom Grad \(2\) in \(n\) Variablen).
Indem wir \(Q\) als Niveauhyperfläche (zum Niveau \(0\)) auffassen, erhalten wir aus 4.9.3 eine Methode, die Tangentialhyperebenen an \(Q\) mit Hilfe des Gradienten von \(f\) zu berechnen.
Dieses Verfahren bildet eine Alternative zu Methoden aus der linearen Algebra.
Die Tangenten an die Ellipse
\( Q=\bigset{\binom xy\in\RR^2}{f\binom xy = 0} \)
mit
\( f\binom xy := \) \( x^2 - \frac12\,x\,y + 2\,y^2 + 3\,x - 10 \)
kann man z.B. berechnen aus
\( \grad f\binom xy \) \( = \left( \begin{array}{l} 2\,x - \frac12\,y + 3 \\ -\frac12\,x + 4\,y \end{array}\right) \).
Die folgende Skizze zeigt einige der Niveaulinien von \(f\); die hier relevante (zum Niveau \(10\)) ist rot hervorgehoben. Dazu sehen Sie in vier interaktiv beweglichen Punkten der Ellipse die Gradienten und orthogonal dazu die Tangenten an die Niveaulinie angedeutet.
In der Startposition (zu der Sie auch durch erneutes Laden der Seite wieder kommen) liegen diese Punkte auf den in den Schnittpunkten der Ellipse mit den Koordinatenachsen.
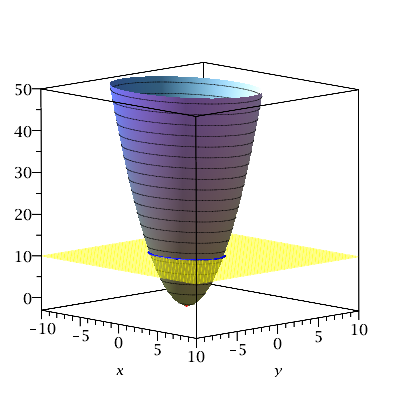
Hier sehen Sie den Graph der Funktion \(f\) (Klick aufs Bild führt zu einer interaktiv beweglichen x3d-Version):
Man kann das eben beschriebene Verfahren auch für allgemeinere Kurven als Kegelschnitte anwenden:
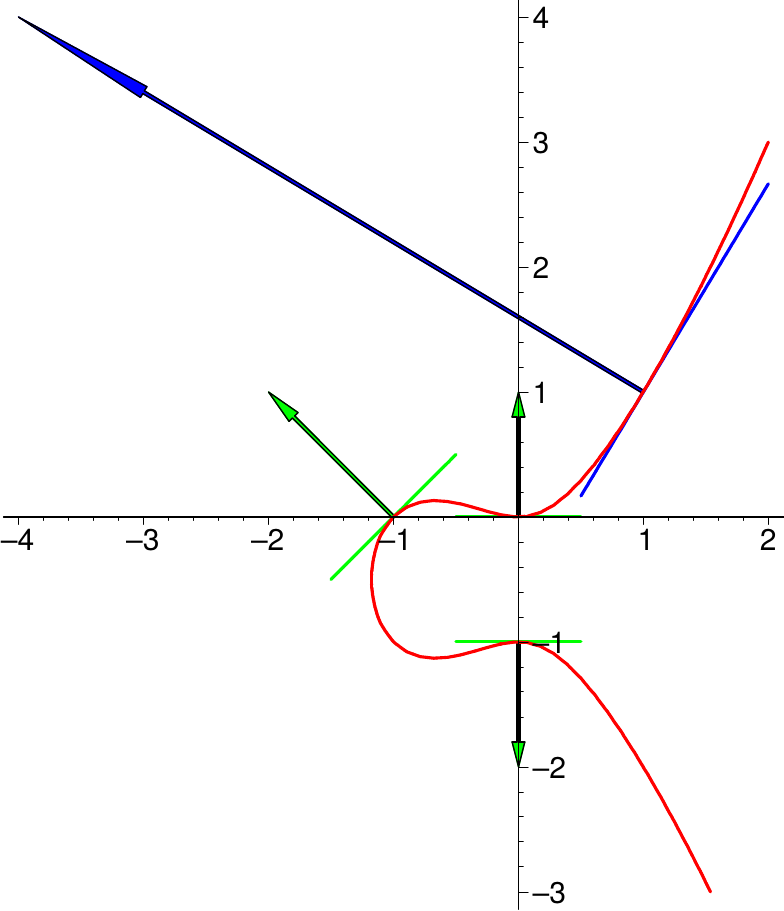
Wir fassen die Kurve
\( C:= \) \( \bigset{\binom xy\in\RR^2}{y^2+y=x^3+x^2} \)
auf als Niveaulinie der Funktion
\( f\colon\RR^2\to\RR\colon \) \( \binom xy\mapsto y^2+y-x^3-x^2 \).
Es gilt \( \grad f\binom xy \) \( = \left( \begin{array}{c} -3\,x^2-2\,x \\ 2\,y + 1 \end{array}\right) \).
Um den Verlauf der Kurve zu skizzieren, verschafft man sich einige Punkte und die zugehörigen Tangenten (über die Gradienten).
So ist etwa \( \binom11 \in C \), mit \( \grad f \binom11 = \binom{-5}3 \).
Die Tangente in diesem Punkt hat also die Richtung \( \frac1{\sqrt{34}} \binom3{5} \) und damit die Steigung \( \frac53 \).
Weitere Punkte von \(C\), in denen die Tangente leicht zu bestimmen ist, sind etwa
\( \binom00 \), \( \binom{-1}0 \), und \( \binom0{-1} \).
Auch den Graphen \( \Gamma(f) \) einer Funktion
\( f\colon D\to\RR\colon \) \( x = \left(\begin{array}{c}x_1^{}\\\vdots\\x_n^{}\end{array}\right) \mapsto f(x) \)
kann man als Niveaumenge einer geeigneten Funktion auffassen:
Wir setzen
\( g\colon D{\color{blue}{\times\RR}}\to\RR\colon \) \( \left(\begin{array}{c}x_1^{}\\\vdots\\x_n^{}\\{\color{blue}{x_{n+1}^{}}}\end{array}\right) \mapsto f(x) % {\color{blue}{{}- x_{n+1}^{}}} \).
Dann gilt
\( \Gamma(f) = \) \( \bigset{ \left(\begin{array}{c} x_1^{}\\\vdots\\x_n^{}\\{\color{blue}{f(x_1^{},\ldots,x_n^{})}} \end{array}\right) } {\left(\begin{array}{c}x_1^{}\\\vdots\\x_n^{}\end{array}\right) \in D} = \) \( \bigset{ \left(\begin{array}{c}x_1^{}\\\vdots\\x_n^{}\\{\color{blue}{x_{n+1}^{}}}\end{array}\right) \in D\times\RR} {\kern-.2em g\left(\begin{array}{c}x_1^{}\\\vdots\\x_n^{}\\{\color{blue}{x_{n+1}^{}}}\end{array}\right) = 0 \kern-.2em } \).
Also ist \( \Gamma(f) \) die Niveaumenge zum Niveau \(0\) für die Funktion \(g\).
Wir nehmen jetzt \(n = 2\) an und betrachten einen Punkt \( a = (a_1^{},a_2^{},{\color{blue}{a_3^{}}})\transp \) auf dem Graphen \( \Gamma(f) \)
— es gilt also \( \color{blue}{a_3^{}=f\binom{a_1^{}}{a_2^{}}} \).
Als Gleichung für die Tangentialebene an diese Niveaumenge erhalten wir:
\( 0 = \) \( \grad g(a)\skalp\left(\begin{array}{c} x_1^{}-a_1^{}\\x_2^{}-a_2^{}\\{\color{blue}{x_3^{}-a_3^{}}} \end{array}\right) \)
\( = g_{x_1}^{}(a)\,(x_1^{}-a_1^{}) \) \( + g_{x_2}^{}(a)\,(x_2^{}-a_2^{}) \) \( + {\color{blue}{g_{x_3}^{}(a)\,(x_3^{}-a_3^{})}} \).
Wegen \( \grad g(a)= \left(\begin{array}{c} f_{x_1}^{}\binom{a_1^{}}{a_2^{}}\\ f_{x_2}^{}\binom{a_1^{}}{a_2^{}} \\{\color{blue}{-1}} \end{array}\right) \) und \(\color{blue}{a_3 = f\binom{a_1}{a_2}}\) entspricht dies der in 4.4.14 angegebenen Darstellung
\( {\color{blue}{x_3^{}}} \) \( = T_1\bigl(f,\binom{x_1^{}}{x_2^{}},\binom{a_1^{}}{a_2^{}}\bigr) \) \( = {\color{blue}{f\binom{a_1^{}}{a_2^{}}}} + \grad f\binom{a_1^{}}{a_2^{}}\skalp \binom{x_1^{}-a_1^{}}{x_2^{}-a_2^{}} \)
\( = {\color{blue}{a_3^{}}} \) \( + f_{x_1}^{}\binom{a_1^{}}{a_2^{}}\,(x_1^{}-a_1^{}) \) \( + f_{x_2}^{}\binom{a_1^{}}{a_2^{}}\,(x_2^{}-a_2^{}) \)
mit Hilfe des Taylorpolynoms erster Stufe.
| ↰ 4.1 | Material | |
| ← 4.8 | HM 2 | 5.1 ↳ |