Das \(\epsilon\)-\(\delta\)-Kriterium

(Den vollständigen Abschnitt 1.10 finden Sie hier.)

1.10.5. Die \(\epsilon\)-\(\delta\)-Beschreibung der Stetigkeit.

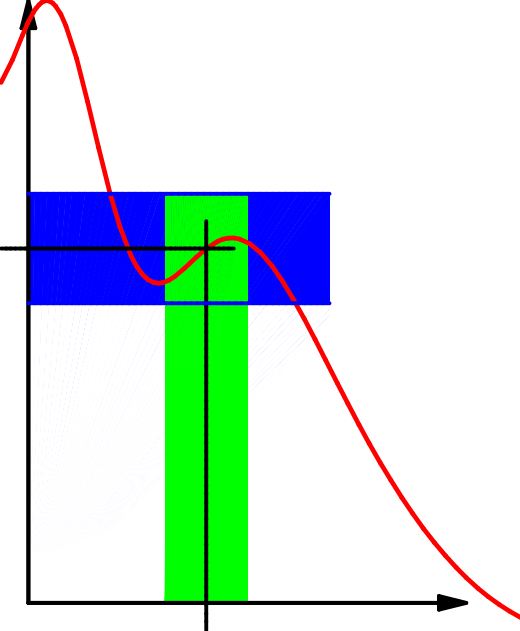
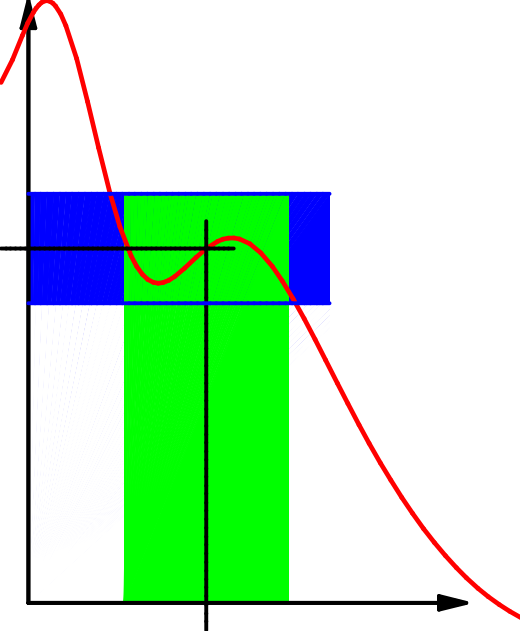
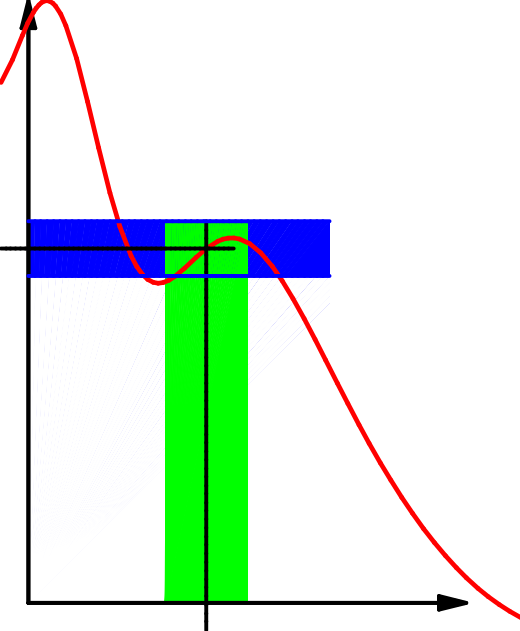
Die Funktion \(f \colon M \to \RR\) ist genau dann stetig im Punkt \(x_0\) wenn gilt:

Dabei wird zuerst die Fehlertoleranz \(\epsilon\) vorgegeben: Die Schranke \(\delta = \delta_\epsilon\) hängt von der Wahl von \(\epsilon\) ab.

Man kann das auch so ausdrücken:

1.10.6. Beschreibung der Stetigkeit durch Umgebungen.

Die Funktion \(f \colon M \to \RR\) ist genau dann stetig im Punkt \(x_0 \in M\), wenn es zu jeder Umgebung \(U = U_\epsilon (f (x_0 ))\) eine Umgebung \(V = U_\delta(x_0)\) derart gibt, dass \(f (V\cap M) \subseteqq U\).

Die Beschreibung durch Umgebungen ist recht anschaulich:

\(x_0\qquad\)	\(x_0\qquad\)	\(x_0\qquad\)
Es gilt hier		aber
\(f\bigl(U_\delta(x_0)\bigr)\subseteq U_\epsilon(f(x_0))\);	\(f\bigl(U_{2\,\delta}(x_0)\bigr)\subseteq U_\epsilon(f(x_0))\);	\(f\bigl(U_\delta(x_0)\bigr) \nsubseteq U_{\frac12\epsilon}(f(x_0))\).

Das gibt es erst, seit wir wegen einer Pandemie rein online lehren:

Sie können hier

• \(\epsilon\) und \(\delta\) modifizieren und versuchen, die Eingangsschranke \(\delta\) an die von Ihnen gewählte Fehlerschranke \(\epsilon\) anzupassen,
• den Punkt \(x_0\) verändern,
• oder zurück zur ersten oder zur zweiten Funktion gehen.

Die hier benutzte Funktion ist übrigens gegeben durch \(f \colon \RR\setminus\{8\} \to \RR \colon {}\)\( x\mapsto f(x) := 5\,\cos(\frac{5}{x-8}) \).