| ↰ 2.1 | Material | 2.7 → |
| ← 2.5 | HM 2 | 3.1 ↳ |
In vielen technischen oder physikalischen Anwendungen werden
Terme höherer Ordnung
ignoriert, um einfachere
(oder überhaupt handhabbare) Formeln zu bekommen.
Den Hintergrund (und die Grundlage für eine Kontrolle des entstehenden Fehlers) bietet der folgende Satz.
Es sei \( f\colon [a,b]\to\RR \) eine \(n + 1\) mal stetig differenzierbare Funktion.
Dann gibt es für jedes Paar \((x,x_0)\) von Zahlen im Intervall \((a,b)\) eine Zahl \( \vartheta_{x,x_0^{}} \) mit \( 0 \lt \vartheta_{x,x_0^{}} \lt 1 \) so, dass gilt:
\( f(x) = \color{blue}{\left( \color{black}{ \sum\limits_{k=0}^n \dfrac{f^{(k)}(x_0^{})}{k!} \, (x-x_0^{})^k } \right)} \) \( + \dfrac{f^{(n+1)}\bigl(x_0^{}+\vartheta_{x,x_0^{}}\,(x-x_0^{})\bigr)}{(n+1)!}\,(x-x_0^{})^{n+1} \).
Man nennt
\( \color{red}{T_n(f,x,x_0^{})} \) \( := \sum\limits_{k=0}^n \dfrac{f^{(k)}(x_0^{})}{k!} \, (x-x_0^{})^k \)
das Taylorpolynom der Stufe \(n\) um den Entwicklungspunkt \(x_0\).
\( \color{red}{R_n(f,x,x_0^{})} \) \( := \dfrac{f^{(n+1)}\bigl(x_0^{}+\vartheta_{x,x_0^{}}\,(x-x_0^{})\bigr)}{(n+1)!}\,(x-x_0^{})^{n+1} \)
wird als Restglied nach Lagrange bezeichnet.
Das Restglied gibt den Fehler an, den man macht, wenn man
statt der komplizierten Funktion \(f\) das (wesentlich einfacher und
billiger auszuwertende) Polynom \(T_n(f,x,x_0^{})\) verwendet.
Um von der Vereinfachung zu profitieren, wird man das
Restglied nicht exakt berechnen, sondern den Fehler
(eventuell ziemlich grob) abschätzen.
Für \(x_0 = 0\) haben Taylorpolynom und Restglied die folgende Gestalt:
\( T_n(f,x,0) = \sum\limits_{k=0}^n \frac{f^{(k)}(0)}{k!}\,x^k \)
\( R_n(f,x,0) = \dfrac{f^{(n+1)}(\vartheta_{x,0}\,x)}{(n+1)!}\,x^{n+1} \).
In der folgenden Darstellung können Sie
durch Einstellen von \(a\), \(b\), \(c\) und \(d\) eine Funktion
\(f\) aus vier gegebenen Funktionen linear kombinieren (ja, ich
nutze hier die Gelegenheit, Sie sachte an die lineare Algebra zu
erinnern), die Stufe des Taylorpolynoms auswählen und den
Entwicklungspunkt \(x_0\) verändern.
Versuchen Sie dann, die Challenge zu meistern!
Wir berechnen das Taylorpolynom der Stufe \(3\) und das zugehörige Restglied für \( f(x)=\sqrt{1+x} \) am Entwicklungspunkt \(x_0 = 0\):
\( f(x) = \phantom{-\frac00\frac11} \,(1+x)^{ \frac12} \)
\( f'(x) = \phantom{-\frac11} \frac12\,(1+x)^{-\frac12} \)
\( f''(x) = \phantom{\frac11} {-\frac14}\,(1+x)^{-\frac32} \)
\( f'''(x) = \phantom{-\frac11} \frac38\,(1+x)^{-\frac52} \)
\( f^{(4)}(x) = \, {-\frac{15}{16}}\,(1+x)^{-\frac72} \)
Daher ist
\( T_3(f,x,0) \) \( = 1 + \frac12\,x - \frac18\,x^2 + \frac1{16}\,x^3 \)
und
\( R_3(f,x,0) \) \( =\dfrac{-5\,x^4}{128\,(1+\vartheta_{x,0}^{}\,x)^{\frac72}} \).
In der folgenden Skizze sieht man den Graph der Funktion
\( f(x)=\sqrt{1+x} \)
sowie die Taylorpolynome
\( T_0(f,x,0) =1 \),
\( T_1(f,x,0) = 1 + \frac12\,x \),
\( T_2(f,x,0) = 1 + \frac12\,x - \frac18\,x^2 \)
und
\( T_3(f,x,0) = 1 + \frac12\,x - \frac18\,x^2 + \frac1{16}\,x^3 \):
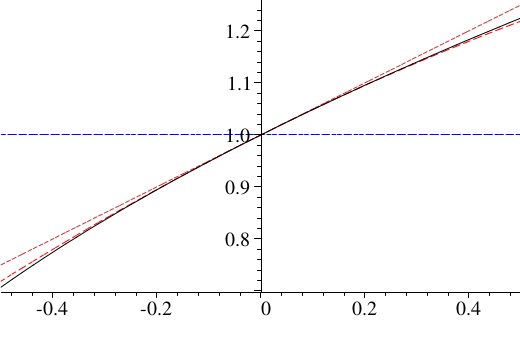
Die Taylorpolynome für die hier vorliegende Funktion sind Partialsummen der binomischen Reihe zum Exponenten \(\alpha=\frac12\) (siehe 1.14.16):
Wegen
\( \binom{\color{red}{1/2}}0=1 \),
\( \binom{\color{red}{1/2}}1=\frac{\color{red}{1/2}}1=\frac12 \),
\( \binom{\color{red}{1/2}}2=\frac{\color{red}{1/2}\,(\color{red}{1/2}-1)}{1\cdot2}=-\frac18 \),
\( \binom{\color{red}{1/2}}3=\frac{\color{red}{1/2}\,(\color{red}{1/2}-1)\,(\color{red}{1/2}-2)}{1\cdot2\cdot3}=\frac1{16} \),
gilt
\( \sum\limits_{n=0}^3 \binom{\color{red}{1/2}} n\,x^n \) \( = 1 + \frac12\,x - \frac18\,x^2 + \frac1{16}\,x^3 \).
Mit steigender Stufe scheinen die Taylorpolynome die gegebene Funktion \(f\) immer besser zu approximieren.
Für viele Funktionen ist das tatsächlich wahr — wir brauchen dazu natürlich mindestens, dass die Funktion beliebig oft differenzierbar ist.
Die Funktion \( f\colon[a,b]\to\RR \) sei beliebig oft differenzierbar.
Für \( x_0^{}\in(a,b) \) heißt dann die Potenzreihe
\( T(f,x,x_0^{}) \) \( :=\sum\limits_{k=0}^\infty \dfrac{f^{(k)}(x_0^{})}{k!}\,(x-x_0^{})^k \)
die Taylorreihe der Funktion \(f\) um den Entwicklungspunkt \(x_0\).
Offenbar gilt:
Die Taylorreihe \( T(f,x,x_0^{}) \) konvergiert für ein gegebenes \(x\) genau dann gegen \(f(x)\), wenn gilt:
\( \lim\limits_{n\to\infty} R_n(f,x,x_0^{}) = 0 \).
Man wird also versuchen, das Intervall \( [a,b] \) so zu wählen, dass für alle \( x\in[a,b] \) das Restglied gegen \(0\) konvergiert — und das auch noch möglichst schnell.
Genauere Untersuchungen finden im Rahmen der Numerik statt.
In den folgenden Skizzen ist außer dem Graph von \(f\) (rot) jeweils das Taylorpolynom \(T_2(f,x,1)\) zweiter Stufe \( \) am Entwicklungspunkt \(x_0 = 1\) (blau) und das Restglied (grün) eingetragen.
Das Restglied gibt den Fehler an, den man in Kauf nimmt, wenn man die Funktion durch das Taylorpolynom ersetzt.
\(
f(x)=\sin(2\,x)
\)

\(
f(x)=\frac14\,\cos(5\,x)
\)
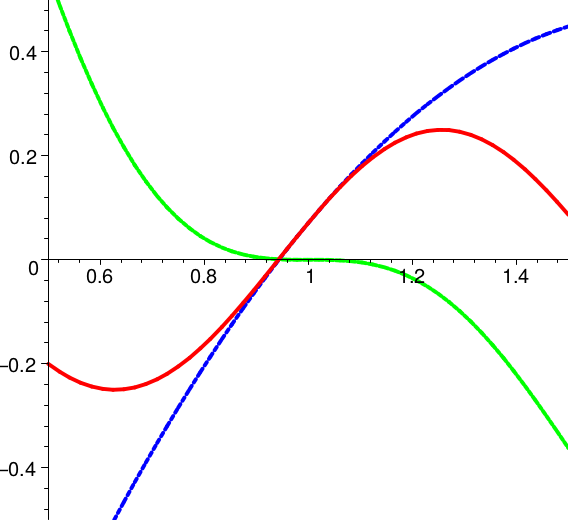
\(
f(x)=\frac{1}{10}\,x^4
\)
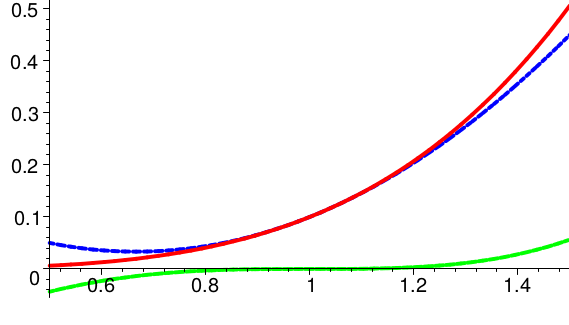
\(
f(x)=\frac{1}{40}\,x^3\,(6\,\ln x-11)+\frac{7}{10}
\)
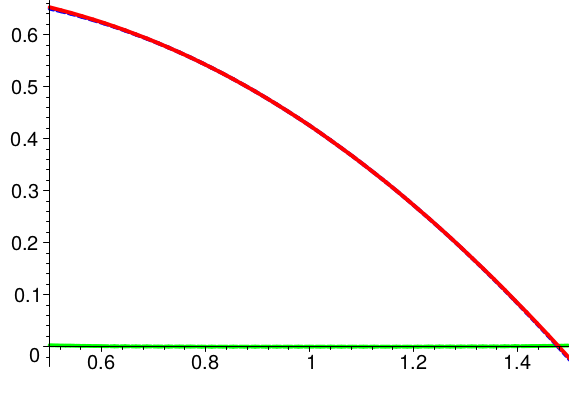
Bei der zuletzt gezeigten Funktion ist die Passung des Taylorpolynoms der Stufe \(2\) in der betrachteten Umgebung erfreulich gut.
Das ist allerdings nur in dieser Umgebung richtig:
\(
f(x)=\frac{1}{40}\,x^3\,(6\,\ln x-11)+\frac{7}{10}
\)
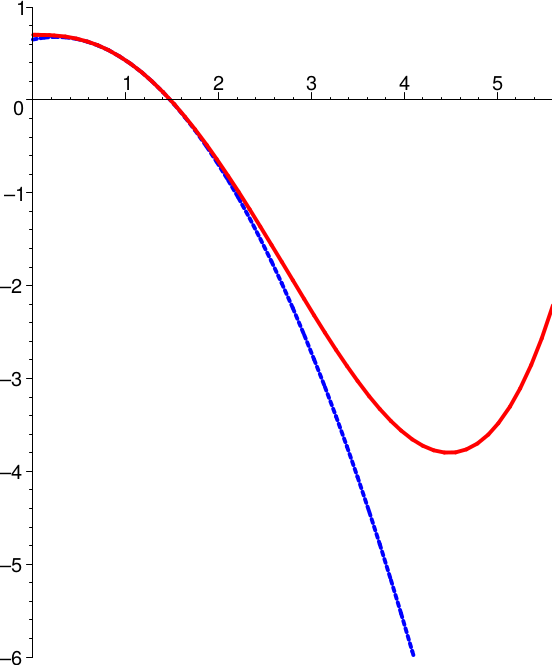
Die dritte Ableitung der betrachteten Funktion ist übrigens
\( f^{(3)}(x) = \frac9{10}\,\ln(x) \),
also nicht mehr stetig nach \(0\) fortsetzbar.
Die Funktionen \( f^{(0)} \), \( f^{(1)} \), \( f^{(2)} \) haben stetige Fortsetzungen an der Stelle \(x = 0\); die Fortsetzungen von \( f^{(0)} \) und \( f^{(1)} \) sind auch differenzierbar in \(x = 0\).
Als Intervall zur Taylorentwicklung müssen wir also ein Intervall \( [a,b] \) mit \(a \gt 0\) wählen.
Dass Taylorpolynome nur in kleinen Umgebungen gut zur gegebenen Funktion passen, ist ein allgemeines Phänomen:
\(
f(x)=\sin(2\,x)
\)
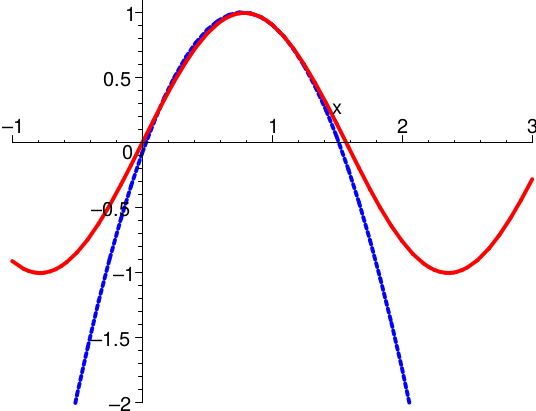
\(
f(x)=\frac14\,\cos(5\,x)
\)

Wenn die Taylorreihe \( T(f,x,x_0^{}) \) einer Funktion \(f\) in einem Intervall gegen \(f (x) \) konvergiert, so wird \(f\) in diesem Intervall durch eine Potenzreihe beschrieben.
Die Koeffizienten sind dann auch eindeutig bestimmt:
Die Funktion \( f\colon (x_0-\rho,x_0+\rho)\to\RR \) werde durch eine (reelle) Potenzreihe dargestellt:
\( f(x) = \sum\limits_{k=0}^\infty a_k\,(x-x_0^{})^k \).
Dabei sei \( \rho \) der Konvergenzradius, also \( (x_0-\rho,x_0+\rho) = \RR \cap U_\rho(x_0^{}) \).
Dann ist \(f\) im Intervall \( (x_0-\rho,x_0+\rho) \) beliebig oft differenzierbar.
Die Koeffizienten der Potenzreihe stimmen mit den Koeffizienten der Taylorreihe überein:
\( \forall\,k\ge0\colon{}\quad \) \( a_k = \frac{f^{(k)}(x_0^{})}{k!} \).
Insbesondere gilt:
Stimmen die durch zwei Potenzreihen
\(
\sum\limits_{k=0}^\infty a_k\,(x-x_0^{})^k
\)
und
\(
\sum\limits_{k=0}^\infty b_k\,(x-x_0^{})^k
\)
definierten Funktionen auf einem nicht leeren, offenen Intervall überein,
so sind alle Koeffizienten gleich:
\( \forall\,k\ge0\colon{}\quad a_k = b_k \).
Im (Beweis für den) Eindeutigkeitssatz für Potenzreihen benutzt man die folgende Tatsache, die auch sonst sehr nützlich ist:
Es sei \( (a_n)_{n\in\NN_0} \) eine Folge reeller Koeffizienten, und es sei \( x_0\in\RR \).
Der Konvergenzradius der Potenzreihe \( \sum\limits_{n=0}^{\infty}a_n(x-x_0)^n \) sei mit \( \rho \) bezeichnet.
Dann ist die Funktion
\( f\colon U_\rho(x_0)\cap\RR\to\RR\pause\colon \) \( x \mapsto \sum\limits_{n=0}^{\infty}a_n(x-x_0)^n \)
beliebig oft differenzierbar, und es gilt
\( f'(x) = \sum\limits_{n=1}^{\infty}a_nn(x-x_0)^{n-1} \) \( = \sum\limits_{k=0}^{\infty}(k+1)a_{k+1}(x-x_0)^k \).
Als wichtigste Eigenschaft der Exponentialfunktion halten wir fest, dass diese die DGL \( \color{red}{f'=f} \) erfüllt.
Diese DGL hat viele Lösungen, die „richtige“ Lösung wird durch die Anfangsbedingung \(\color{blue}{f (0) = 1}\) ausgewählt.
Durch diese beiden Eigenschaften allein ist die Exponentialfunktion aber auch schon eindeutig festgelegt:
Es ergibt sich die Taylorreihe
\( T(f,x,0) \) \( = \sum\limits_{k=0}^\infty\frac{f^{(k)}(0)}{k!}\, x^k \) \( = \sum\limits_{k=0}^\infty\frac{1}{k!}\, x^k \).
Wir wollen aber auch überpüfen, ob diese Potenzreihe wirklich die gewünschte Funktion darstellt (siehe 2.6.12 als warnendes Beispiel).
Wegen \( 0\leqq\vartheta_{x,0} \lt 1 \) gilt \( \vartheta_{x,0}\,x\in[-|x|,|x|] \).
Da \(f^{(n)} =f\) differenzierbar und deswegen stetig ist, existiert \( m_x := \max\bigset{|f(t)|}{ t\in[-|x|,|x|]} \), nach dem Satz vom Maximum und Minimum 1.13.12, und es gilt \( |f(\vartheta_{x,0}\,x)|\le m_x \).
Damit sehen wir, dass die Folge der Restglieder konvergiert:
\( \left|R_n(f,x,0)\right| \) \( = \left| \dfrac {f^{\color{blue}{(n+1)}}(\vartheta_{x,0}\,x)} {(n+1)!} \,x^{n+1} \right| \) \( = \left| \dfrac {f(\vartheta_{x,0}\,x)} {(n+1)!} \,x^{n+1} \right| \) \( \le m_x\,\dfrac{|x|^{n+1}}{(n+1)!} \) \( \quad \konv[n\to\infty]\quad 0 \).
Also wird \(f\) durch die Potenzreihe \(\exp\) dargestellt:
\( \forall\,x\in\RR\colon{}\quad \) \( \color{red}{f(x)} \) \( = \color{red}{\sum\limits_{k=0}^\infty\frac{1}{k!}\, x^k} \) \( = \exp(x) \) \( = \E^x \).
Damit ist auch unsere Definition 1.14.10 der Exponentialfunktion im Komplexen gerechtfertigt.
Analog zeigt man ausgehend von der Differentialgleichung \( f''=-f \) (die sowohl \(\cos\) als auch \(\sin\) erfüllen) sowie den Anfangsbedingungen \( f(0)=0 \) und \( f'(0)=1 \) (die den Sinus unter den Lösungen der Differentialgleichung auszeichnen), dass die Funktion \(\sin\) (und analog \(\cos\)) tatsächlich durch die in 1.14.17 angegebene Potenzreihe beschrieben wird.
Es kommt vor, dass die Taylorreihe einer Funktion an einer Stelle \(x\) zwar konvergiert, aber nicht gegen den Funktionswert \(f (x) \):
Die Funktion \( f\colon\RR\setminus\{0\}\to\RR \) sei gegeben durch
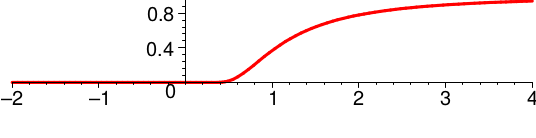
\( f(x) = \) \( \begin{cases} \exp\left(-\frac1{x^2}\right) & \text{ falls $x\gt0$,} \\ \phantom{\exp} 0 & \text{ falls $x\lt0$.} \end{cases} \)
Diese Funktion ist in die „Klebestelle“ \(x_0 = 0\) hinein stetig fortsetzbar durch \( f(0):=0 \).
Die Fortsetzung ist dann beliebig oft differenzierbar, es gilt \( f^{(k)}(0)=0 \) für alle \(k\).
Alle Koeffizienten der Taylorreihe \( T(f,x,0) \) sind also Null, und \( T(f,x,0) \) beschreibt die Nullfunktion: Das ist nicht \(f\).
Wir betrachten \( f\colon\left[-\frac12,1\right]\to\RR\colon x\mapsto\ln(1+x) \).
Mit Hilfe vollständiger Induktion zeigt man
\( \forall\, k\ge1\colon{} \quad \) \( f^{(k)}(x) = (-1)^{k-1}\,\dfrac{(k-1)!}{(1+x)^k} \).
Somit ergibt sich die Taylorreihe als \( T(f,x,0) = \) \( \ln (1) \) \(+ \sum\limits_{n=1}^\infty (-1)^{n-1}\,\dfrac{(n-1)!}{n!\,(1+0)^n}\,x^n \) \( = \sum\limits_{n=1}^\infty (-1)^{n-1}\,\dfrac{x^n}{n} \).
Das Restglied ist
\( R_n(f,x,0) \) \( = \frac{f^{(n+1)}(\vartheta\,x)}{(n+1)!}\,\,x^{n+1} \) \( = \frac{(-1)^n\,n!\,\,\,\,x^{n+1}}{(1+\vartheta\,x)^{n+1}\,(n+1)!} \) \( = \frac{(-1)^n}{n+1}\, \left(\frac{x}{1+\vartheta\,x}\right)^{n+1} \)
mit \( \vartheta:=\vartheta_{x,0} \).
Für \( 0\le x\le1 \) gilt \( \left|\frac{x}{1+\vartheta\,x}\right| \le 1 \).
Für \( -\frac12\le x \lt 0 \) erhält man \( |x|=-x \) \( \le \frac12 \) \( \le 1+x \) \( \lt 1+\vartheta\,x \) und damit wieder \( \left|\frac x{1+\vartheta\,x}\right|\le 1 \,, \quad \)
in jedem Fall also \( \bigl|R_n(f,x,0)\bigr| \pause % \le \frac1{n+1} \).
Folglich konvergiert das Restglied für jedes \(x\in[-\frac12,1]\) gegen \(0\), und die Taylorreihe stellt \(f\) dar (auf dem ganzen Intervall \([-\frac12,1]\)).
Setzt man in die Potenzreihe
\( \ln(1+x) = \) \( \sum\limits_{n=1}^\infty (-1)^{n-1}\,\dfrac{x^n}{n} \)
den Wert \(x = 1\) ein, so erhält man
\( \ln 2 \) \( = \ln(1+1) \) \( = 1 - \frac12 + \frac13 - \frac14 + \frac 15 - \cdots \)
Damit haben wir die Summe der alternierenden harmonischen Reihe bestimmt!
| ↰ 2.1 | Material | 2.7 → |
| ← 2.5 | HM 2 | 3.1 ↳ |