\( f\colon[-\frac32,\frac52]\to\RR\colon x\mapsto \frac32\,x^2 - 2\,x \)
— also \( F\in\int f(x)\diff x \):
| ↰ 3.1 | Material | 3.3 → |
| ← 3.1 | HM 2 | 4.1 ↳ |
Es sei \(I\) ein Intervall. Wir nehmen an, dass \( f\colon I\to\RR \) und \( g\colon I\to\RR \) Stammfunktionen besitzen.
Dann besitzen auch \(f + g\) und \( \alpha f \) (für \( \alpha\in\RR\setminus\{0\} \)) Stammfunktionen, und es gilt:
Mit Stammfunktionen \(F\) für \(f\) und \(G\) für \(g\) (und \(F + G\) für \(f + g\)) kann man das auch so schreiben:
Man verifiziert dies durch Differentiation— wir erinnern daran, dass
\(
[A] = [B ]
\)
gerade bedeutet, dass \(A\) und \(B\) dieselbe Ableitung haben
(und sich also nur durch eine additive Konstante unterscheiden).
Hier werden Mengen von Funktionen addiert bzw. mit einem Skalar
multipliziert:
Dies geschieht elementweise, es gilt
\(
[F]+[G] = \bigset{F+c}{c\in\RR} + \pause\bigset{G+d}{d\in\RR}
\)
\(
= \bigset{F+G+k}{k\in\RR}
\)
\(
= [F+G]
\)
und
\(
\alpha\,[F] = \bigset{\alpha\,(F+c)}{c\in\RR}
\)
\(
= \bigset{\alpha\,F+d}{d\in\RR}
\)
\(
= [\alpha\,F]
\).
Wir haben \(\alpha\ne0\) verlangt, damit die Menge \(\alpha[F]\)
nicht zu einer Menge mit nur einem Element (nämlich der Nullfunktion
kollabiert
— in der Tat ist
\(0\cdot[F] = \{0\}\) \(\ne [0\cdot F] = \set{0+c}{c\in\RR}\) \(=\set{c}{c\in\RR}\);
die letzte Menge ist die Menge aller konstanten Funktionen (das sind unendlich viele).
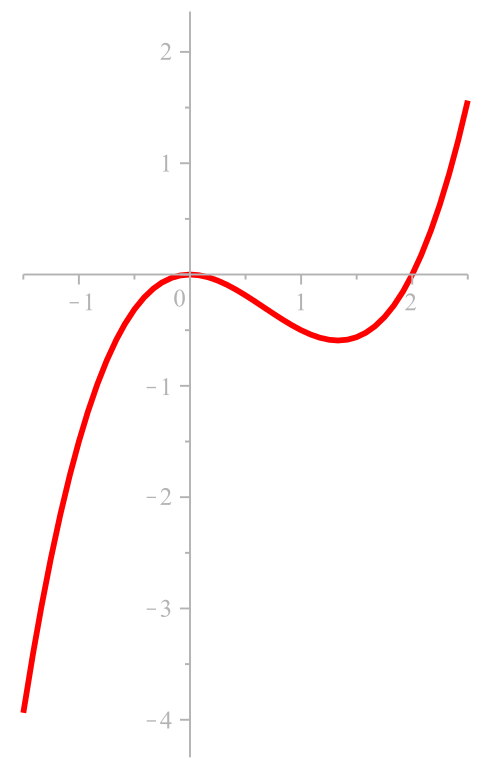
Eine Stammfunktion \(F\) zu
\(
f\colon[-\frac32,\frac52]\to\RR\colon x\mapsto \frac32\,x^2 - 2\,x
\)
— also
\(
F\in\int f(x)\diff x
\):
und die Funktion \( G:=\frac12\,F \)
— also
\(
G\in\frac12\int f(x)\diff x
\):
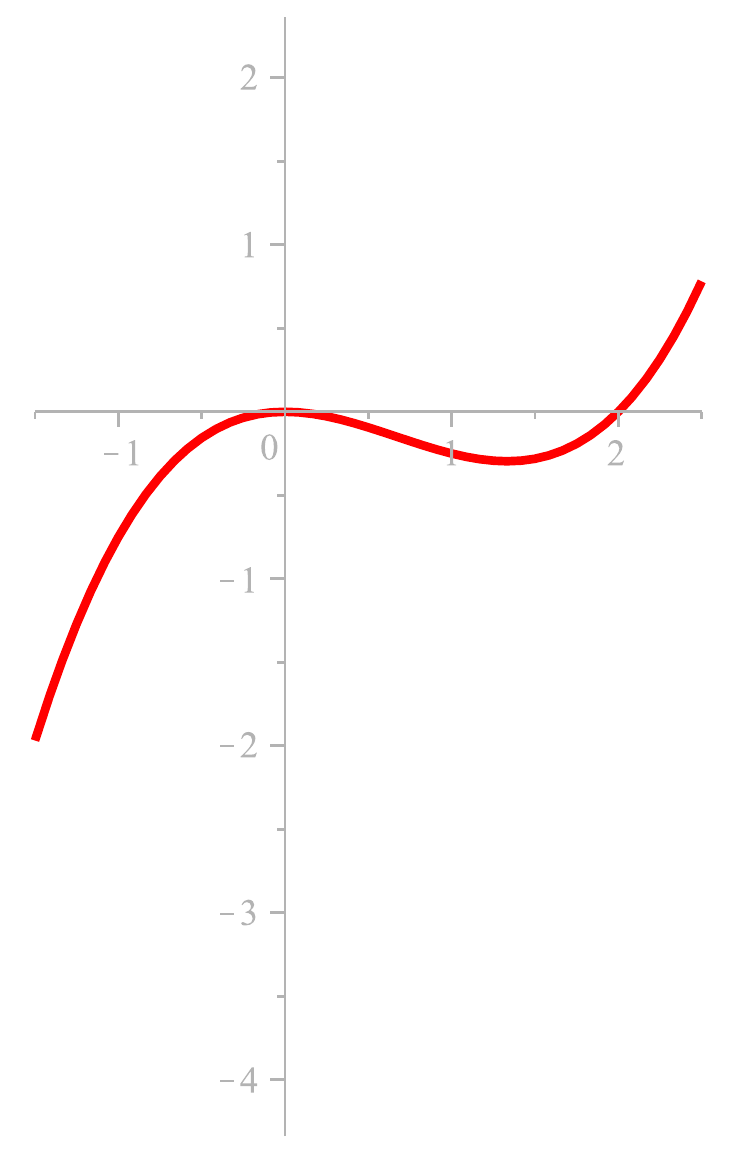
Mehrere Elemente aus
\(
[F]=\ds\int f(x)\diff x
\):
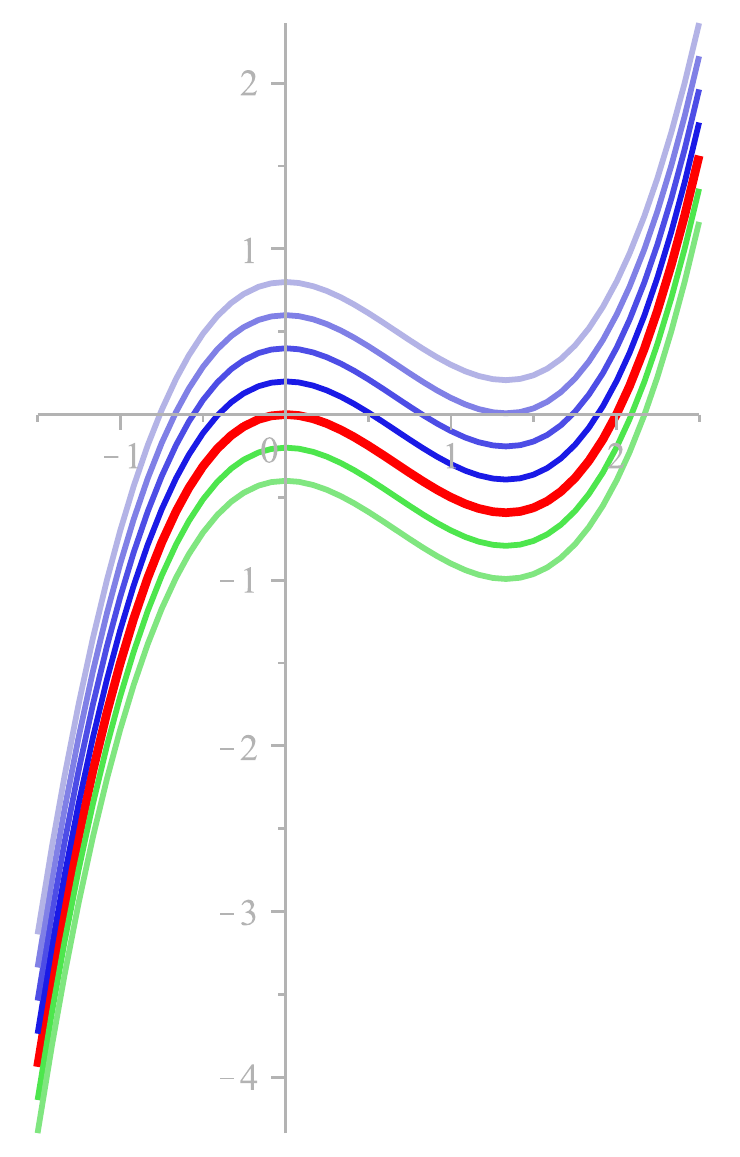
und mehrere Elemente aus
\(
[G]=\frac12[F]
\):
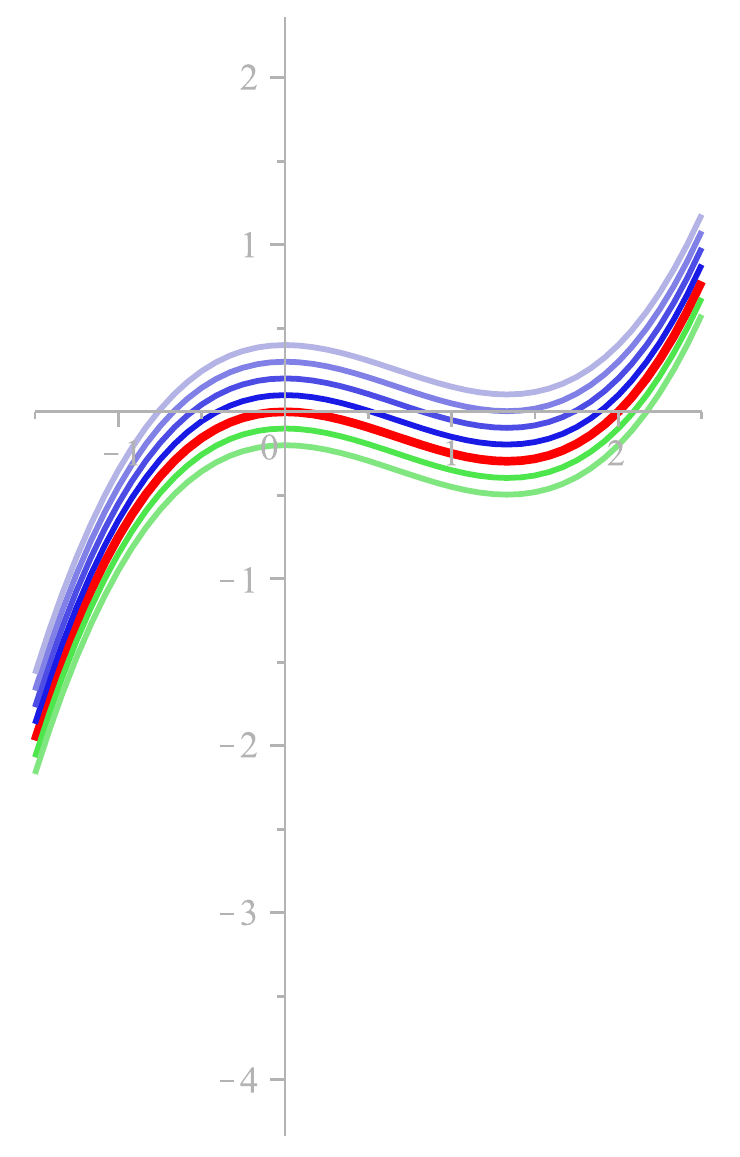
Vielleicht geht es Ihnen wie mir:
am Rand (wo die Funktion steil ansteigt) sieht es nicht so aus, als wären die Funktionsgraphen nur
vertikal verschoben; das wirkt enger gedrängt.
Das ist eine optische Täuschung (ich vermute, weil wir die Tendenz
haben, orthogonal zur Linie zu messen
).
Bewegen Sie in der folgenden Skizze die Punkte \(x\) und \(c\):
Sind \(f\) und \(g\) differenzierbar, so gilt \( \int f'(x)\cdot g(x)\,\diff x \) \( = \bigl[f(x)\cdot g(x)\bigr] - \int f(x)\cdot g'(x) \,\diff x \).
Beweis (durch Nachrechnen/Probe):
Wir leiten die rechte Seite ab:
Mit Hilfe der Produktregel ergibt sich
\( \left(f'(x)\cdot g(x) + f(x)\cdot g'(x)\right) \) \( - f(x)\cdot g'(x) \) \( = f'(x)\cdot g(x) \)
— das ist die Ableitung der linken Seite.
Eine Stammfunktion für \( x\,\E^x \) erhalten wir mit partieller Integration:
Wir setzen \(g(x ) := x\) und \(f (x ) := \E^x\) (also \( f'(x)= \E^x \)), dann gilt
\( \int x\,\E^x \,\diff x \) \( = \bigl[ x\,\E^x\bigr] -\int 1\cdot \E^x\,\diff x \) \( = \bigl[ (x-1)\,\E^x\bigr] \).
Probe: Man verifiziert
\( \diffAt{(t-1)\,\E^t}{t}{x}^{\vphantom X} \) \( = (x-1)\, \E^x + 1\cdot \E^x \) \( = x\,\E^x \)
[Produktregel].
Eine Stammfunktion von \( \cos x\cdot \sin x \) findet man durch den Ansatz \( g(x ) := \sin x \) und \( f (x ) := \sin x \) (also \(f' (x ) = \cos x \)):
\( \int \cos x\cdot \sin x \,\diff x \) \( = \bigl[ \sin x\cdot\sin x \bigr] - \int \sin x\cdot\cos x \,\diff x \)
liefert \( 2\,\int \cos x\cdot \sin x \,\diff x \) \( = \left[ (\sin x)^2 \right] \), also \( \int \cos x\cdot \sin x \,\diff x \) \( = \left[ \frac12\,(\sin x)^2 \right] \).
Die Probe überlasse ich Ihnen ...
| ↰ 3.1 | Material | 3.3 → |
| ← 3.1 | HM 2 | 4.1 ↳ |