| ↰ 4.1 | Material | 4.7 → |
| ← 4.5 | HM 2 | 5.1 ↳ |
Bei der Bestimmung von Extrema für Funktionen mehrerer Veränderlicher will man häufig die Suche beschränken auf eine „dünne“ Teilmenge des Definitionsbereichs der Funktion
(etwa auf die Oberfläche eines Körpers in \( \RR^3 \), oder den Rand einer Teilmenge von \( \RR^2 \)).
Gegeben sei eine stetige Funktion \( f\colon\RR^2\to\RR \) sowie die Ellipse \( E:= \) \( \bigset{\binom{x_1^{}}{x_2^{}}}{\frac{x_1^2}{\alpha^2}+\frac{x_2^2}{\beta^2}-1=0} \).
Wir interessieren uns für die folgenden Fragen:
Die Existenz von Extrema folgt in diesem Fall aus dem Satz vom Minimum und Maximum 4.2.18 [weil \(E\) kompakt ist].
Das explizite Auffinden der Extrema gestaltet sich schwierig.
Eine Möglichkeit wäre, die Ellipse zu parametrisieren (also etwa die Gleichung der Ellipse nach \(x_1\) auflösen und dann die Ellipse zu beschreiben als
\( E = \) \( \bigset{\binom{x_1^{}}{g(x_1^{})}}{x_1^{}\in I} \)
— das geht aber nicht auf einmal, man muss wegen der auftretenden Wurzel die Ellipse aus zwei Hälften zusammensetzen):
Dann betrachten wir \( \tilde g(t):=\binom{t}{g(t)} \) und können die Komposition \( f\circ\tilde g\colon I\to\RR \) auf Extrema untersuchen.
Eine bessere Parametrisierung der Ellipse erhält man als \( p\colon[0,2\,\pi]\to\RR^2\colon \) \( t\mapsto \binom{\alpha\,\cos t}{\beta\,\sin t} \).
Um die Extrema einer differenzierbaren Funktion \(f\) auf der Ellipse zu finden, kann man also die Komposition \( f\circ p \) untersuchen.
So schöne Parametrisierungen darf man aber bei beliebigen Rändern nicht erwarten!
Zur Bestimmung von Extrema unter Nebenbedingungen gibt es eine Methode, die die Parametrisierung der durch die Nebenbedingung festgelegten Menge vermeidet und dadurch zweckmäßiger ist.
Wir werden unsere Nebenbedingung als Nullstellenmenge einer Funktion \(g\) beschreiben und nach Extremalstellen für \(f\) in der Menge \( \set{x\in D}{g(x)=0} \) suchen.
Es sei \( D\subseteq\RR^n \) offen und \( f,g\in\Cf1D \).
Der Punkt \( a\in D \) erfülle \(g(a) = 0\) und \( \grad g(a)\ne0 \).
Dann gilt:
Ist \( \bigl(a,f(a)\bigr) \) ein relatives Extremum für die eingeschränkte Funktion
\( f|_{\set{x\in D}{g(x)=0}}\colon \) \( \set{x\in D}{g(x)=0} \to\RR\colon \) \( x\mapsto f(x) \),
dann gibt es \( \lambda\in\RR \) so, dass gilt:
\( \alert{ \grad f(a) + \lambda\,\grad g(a) = 0 } \).
Mit anderen Worten:
Für jede Variable \(x_k\)
(mit \(1\le k\le n\)) gilt
\(
f_{x_k}(a) + \lambda\,g_{x_k}(a) = 0
\).
Man nennt die Stellen, an denen die Nebenbedingung \( g(x)=0 \) und die Multiplikator-Bedingung \( \grad f(x)+\lambda\grad g(x)=0 \) erfüllt sind, wieder kritische Stellen.
Die Multiplikatormethode gibt nur ein notwendiges Kriterium für das Vorliegen einer Extremalstelle.
Man muss für jede kritische Stelle durch zusätzliche Überlegungen klären, ob tatsächlich ein (relatives) Extremum gefunden wurde.
Wir suchen Extrema der Funktion \( f\colon\RR^2\to\RR\colon \) \( \binom xy \mapsto x\,y^2 \) auf der Ellipse \( E= \) \( \bigset{\binom xy\in\RR^2}{\frac{x^2}3+\frac{y^2}4=1} \), also unter der Nebenbedingung \( g\binom xy=0 \) mit \( g\colon\RR^2\to\RR\colon \) \( \binom xy\mapsto \frac{x^2}3+\frac{y^2}4 - 1 \).
Wir berechnen \( \grad f\binom xy \pause = \binom{y^2}{ 2xy} \) und \( \grad g\binom xy = \binom{\frac{2}3\,x}{\frac 12\,y} \).
Kritische Stellen (also Kandidaten für Extremalstellen) ergeben sich als Lösungen des (nicht linearen) Gleichungssystems
Hier sind \(x\), \(y\) und \(\lambda\) als Unbestimmte anzusehen!
Ist \( y\ne0 \), so liefert Gleichung (3) die Beziehung \( \lambda=-4\,x \).
Setzt man dies in (2) ein, erhält man \( y^2 - \frac83\,x^2 = 0 \).
Zusammen mit (1) folgt \(x^2 = 1\) und damit \( y^2=\frac83 \).
Dies liefert die Kandidaten \( P_1 = \binom{\phantom-1}{\phantom-\frac23\sqrt6} \), \( P_2 = \binom{\phantom-1}{-\frac23\sqrt6} \), \( P_3 = \binom{-1}{\phantom-\frac23\sqrt6} \), \( P_4 = \binom{-1}{-\frac23\sqrt6} \).
Es bleibt noch der Fall \(y = 0\) zu betrachten:
Dann ist \( x^2=3 \) und \( \lambda=0 \).
Weitere Kandidaten sind also \( P_5 = \binom{\sqrt3}{0} \), \( P_6 = \binom{-\sqrt3}{\phantom-0} \).
Die Menge \(E\) ist kompakt, und die Einschränkung \(f |_E\) der Funktion \(f\) auf \(E\) ist stetig.
Nach dem Satz vom Maximum und Minimum 4.2.18 besitzt \(f |_E\) ein globales Maximum und ein globales Minimum auf \(E\).
Alle diese Extrema finden sich unter den eben als Kandidaten bestimmten kritischen Stellen. Wir sehen uns die Funktionswerte an diesen Stellen an:
| \( P_1 \) | \( P_2 \) | \( P_3 \) | \( P_4 \) | \( P_5 \) | \( P_6 \) | |
| \( f(P_j) \) | \( \frac{24}9 \) | \( \frac{24}9 \) | \( -\frac{24}9 \) | \( -\frac{24}9 \) | \( 0 \) | \( 0 \) |
Offenbar liegen bei \(P_1\) und \(P_2\) Maxima vor, bei \(P_3\) und \(P_4\) dagegen Minima.
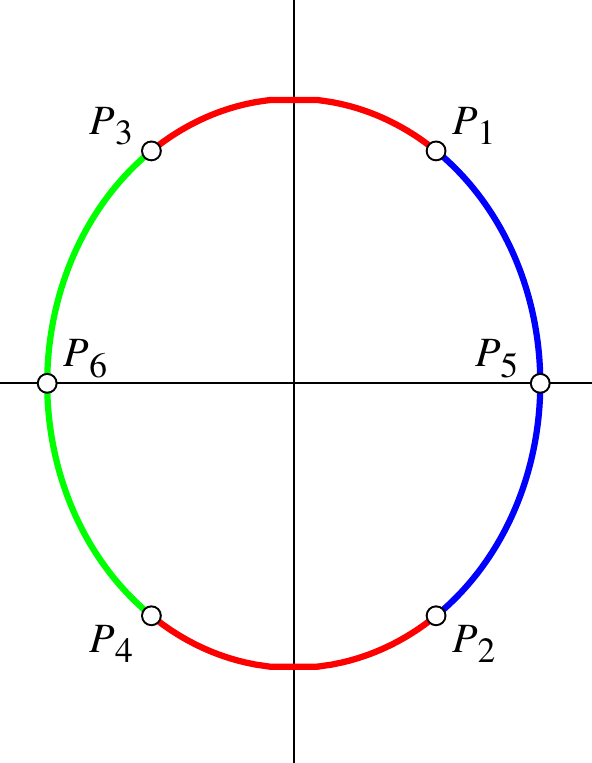
Die Stellen \(P_5\) und \(P_6\) sind relative Extremalstellen:
Um dies einzusehen, beachtet man die Reihenfolge der kritischen Stellen auf der Ellipse:
Auf dem Ellipsenbogen \(B\), der von \(P_2\) und \(P_1\) begrenzt wird und \(P_5\) enthält, liegt keine weitere kritische Stelle.
Da auch \(B\) kompakt ist, nimmt die Einschränkung \(f |_B\) ein Minimum an:
Dies muss bei \(P_5\) liegen.
Ebenso argumentiert man auf dem Bogen, der von \(P_3\) und \(P_4\) begrenzt wird und \(P_6\) enthält.
In den folgenden beiden Skizzen sehen Sie jeweils einen Ausschnitt des Graphen der Funktion \( f \colon\RR^2\to\RR\colon \) \( \binom xy \mapsto x\,y^2 \) angedeutet (als Fläche im Raum — denken Sie an eine Gebirgsoberfläche).
In der \(x\)-\(y\)-Ebene stellen wir den Definitionsbereich dar, darin liegt die Ellipse \( E= \) \( \bigset{\binom xy\in\RR^2}{\frac{x^2}3+\frac{y^2}4=1} \).
Die Suche nach Maxima und Minima von Funktionswerten \(f\binom xy\) unter der Nebenbedingung \(\binom xy\in E\) können Sie sich so veranschaulichen:
Man wandert im Gebirge (also auf dem Graph von \(f\)) entlang eines Wegs (in der linken Skizze gelb dargestellt), dessen Grundriss (in einer Wanderkarte, um im Bild zu bleiben) die Ellipse \(E\) ist.
Jetzt will man wissen, wo man den höchsten Punkt auf der Tour erreicht, und wo den niedrigsten.
Sie können den dicken roten Punkt im Kreis um die erste Skizze bewegen — abhängig davon bewegt sich (in beiden Skizzen gleichzeitig) eine Stelle \(\binom xy\) auf \(E\) und der darüber (bzw. darunter) liegende Punkt \((x,y,f\binom xy)\transp\) auf dem Graphen.
In der rechten Skizze wurde die Wand
zwischen der
\(x\)-\(y\)-Ebene und dem Wanderweg auf dem Graphen ausgefüllt und
mit den Farben markiert, die bereits in
der früheren Skizze der Ellipse
verwendet wurden.
Die durch die Multiplikator-Methode gefundenen Extrema liegen also wieder bei den Stellen, an denen die Farbe wechselt.
Erhält man mit Hilfe der Multiplikatormethode nur endlich viele kritische Stellen und ist die Menge
\( H:=\bigset{x\in D}{g(x)=0} \)
kompakt, so findet man die relativen Extrema wie in 4.6.5 durch Berechnung und Vergleich der Funktionswerte bei den kritischen Stellen.
Gegebenenfalls muss man (nach der Klärung der absoluten Extrema) die Suche auch wieder auf geeignete Teile von \(H\) beschränken (wie im Beispiel 4.6.5, wo die Rolle der Menge \(H\) durch die Ellipse \(E\) eingenommen wird).
Die Multiplikatormethode 4.6.3 kann man auch anwenden, wenn die Nebenbedingung durch mehrere Gleichungen gegeben ist:
Es sei \( D\subseteq\RR^n \) mit \( D=\inn D \).
Wir wollen die Extrema einer Funktion \( f\in\Cf1D \) unter den Nebenbedingungen \( g_j^{}(x)=0 \) für \( 1 \le j \le k \) bestimmen — also unter mehreren Nebenbedingungen.
Dabei sei \(k \lt n\) und \( g_j^{}\in\Cf1D \) für jedes \(j\).
Für \( a\in D \) schreiben wir
\( \Jac ga:=\left(\begin{array}{c} \grad g_1^{}(a)\transp \\ \vdots \\ \grad g_k^{}(a)\transp \end{array}\right) \),
dabei wird jeweils \( \grad g_j(a) \) als ein Spaltenvektor aufgefasst.
Schließlich setzen wir \( N:= \) \( \bigset{x\in D}{\forall j\le k\colon g_j^{}(x)=0} \) \( =\bigcap\limits_{j=1}^k\bigset{x\in D}{g_j^{}(x)=0} \).
Mit den eben festgelegten Bezeichnungen sei \( a\in N \) (also ein Punkt von \(D\), der allen Nebenbedingungen genügt).
Außerdem habe die Matrix \( \Jac ga \) den vollen Rang \(k\).
Ist nun \( \bigl(a,f(a)\bigr)\transp \) ein relatives Extremum für die eingeschränkte Funktion
\( f|_{N}\colon N \to\RR\colon \) \( x\mapsto f(x) \),
dann gibt es Multiplikatoren \( \lambda_1^{},\ldots,\lambda_k^{}\in\RR \) so, dass gilt:
\( 0 = \) \( \grad f(a) + \sum\limits_{j=1}^k \lambda_j^{}\,\grad g_j^{}(a) \).
Radikal in ihre Bestandteile zerlegt, lautet die Bedingung:
\( \forall\, \ell\le n\colon \) \( f_{x_\ell^{}}(a) + \sum\limits_{j=1}^k \lambda_j^{}\,\bigl(g_{j}^{}\bigr)_{x_\ell^{}}^{}(a) =0 \).
| ↰ 4.1 | Material | 4.7 → |
| ← 4.5 | HM 2 | 5.1 ↳ |