2.3. Differentiation von Umkehrfunktionen

2.3.1. Satz.

Es sei $f:[a,b]\to \mathbb{R}$ streng monoton und stetig.

Dann existiert die Umkehrabbildung $f^{-1}:f([a,b])\to [a,b]$ nach 1.13.11.

Ist $f$ an der Stelle $x_0\in (a,b)$ differenzierbar mit $f^{\prime }(x_0^{})\ne 0$, so ist die Umkehrabbildung $f^{-1}$ differenzierbar an der Stelle $f(x_0)$, und es gilt $\frac{\mathrm{d}}{\mathrm{d}y}{\phantom{\frac{0}{0}}{f}^{-1}(y)|}_{y=f(x_0^{})}$ $=\frac{1}{f^{\prime }(x_0^{})}$.

Geometrischer Beweis der Differentiationsregel für Umkehrfunktionen.

Den Graphen der Umkehrfunktion erhält man durch Spiegeln des Graphen von $f$ an der Winkelhalbierenden.

Dabei wird die Tangente (an den Graph von $f$) im Punkt $(x_0^{},f(x_0^{}))$ in die Tangente (an den Graph $f^{-1}$) im Punkt $(f(x_0^{}),x_0^{})$ übergeführt.

Wir sollten also die Steigung $m$ einer Geraden $g=\left\{(x,y)\in {\mathbb{R}}^2|\phantom{(x,y)\in {\mathbb{R}}^2}\phantom{y=mx+t}y=mx+t\right\}$ mit der Steigung $m^{\ast }$ des Spiegelbildes $g^{\ast }=\left\{(x,y)\in {\mathbb{R}}^2|\phantom{(x,y)\in {\mathbb{R}}^2}\phantom{y=m^{\ast }x+t^{\ast }}y=m^{\ast }x+t^{\ast }\right\}$ von $g$ in Bezug bringen.

Dazu spiegeln wir die Punkte $(0,t),(1,m+t)\in g$ und erhalten $g^{\ast }$ als Verbindungsgerade von $(t,0)$ und $(m+t,1)$.

Wir lösen das Gleichungssystem

$\begin{array}{rlcccl}{m}^{\ast }& t& +& t^{\ast }& =& 0\\ m^{\ast }& (m+t)& +& t^{\ast }& =& 1\end{array}$

und erhalten $m^{\ast }=\frac{1}{m}$ sowie $t^{\ast }=-\frac{t}{m}$.

Damit erhalten wir:

Aus der Steigung $f^{\prime }(x_0^{})$ der Tangente an $f$ in $(x_0^{},f(x_0^{}))$ wird die Steigung

$\frac{\mathrm{d}}{\mathrm{d}y}{\phantom{\frac{0}{0}}{f}^{-1}(y)|}_{y=f(x_0^{})}=\frac{1}{f^{\prime }(x_0^{})}$

der Tangente an $f^{-1}$ im Punkt $(f(x_0^{}),x_0^{})$.

In der folgenden Skizze können Sie interaktiv die Stelle $x_0$ ändern. Das Tangente, das Steigungsdreieck und die Spiegelbilder ändern sich mit.
(Was passiert an den Rändern des Definitionsbereichs $a,b$ ? Bewegen Sie die Stelle $x_0$ auf $a$ bzw. $b$.)

Der geometrische Beweis ist anschaulich, hat aber das Manko, dass die Differenzierbarkeit der Umkehrfunktion (d.h. die Existenz der Tangente) bereits vorausgesetzt wird.
Abhilfe schafft ein analytischer Beweis.

2.3.2. Beispiel.

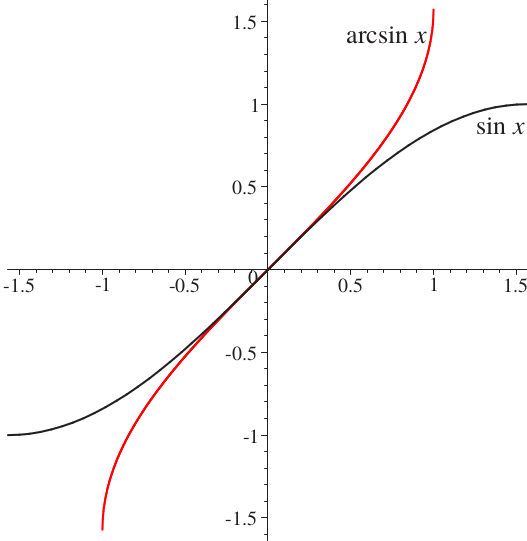
Die Funktion $f:x\mapsto \sin x$ ist im Intervall $[-\frac{\pi }{2},\frac{\pi }{2}]$ streng monoton wachsend und stetig, außerdem differenzierbar im Innern des Intervalls, mit $f^{\prime }(x)=\cos x\ne 0$ für alle $x\in (-\frac{\pi }{2},\frac{\pi }{2})$.

Deswegen existiert die Umkehrfunktion $f^{-1}:[-1,1]\to [-\frac{\pi }{2},\frac{\pi }{2}]:$ $x\mapsto \arcsin x$.

Satz 2.3.1 ergibt für $y_0=\sin (x_0^{})$:

$\frac{\mathrm{d}}{\mathrm{d}y}{\phantom{\frac{0}{0}}\arcsin y|}_{y=y_0}$ $={\displaystyle \frac{1}{\frac{\mathrm{d}}{\mathrm{d}x}{\phantom{\frac{0}{0}}\sin x|}_{x=x_0^{}}}}$ $={\displaystyle \frac{1}{\cos x_0^{}}}$ $={\displaystyle \frac{1}{\sqrt{1-(\sin x_0^{}{)}^2}}}$ $={\displaystyle \frac{1}{\sqrt{1-y_0^2}}}$.

Wir haben damit gezeigt:
Die Umkehrfunktion Arcussinus (kurz $\arcsin$) des Sinus ist definiert im Intervall $[-1,1]$ und differenzierbar im Innern $(-1,1$) dieses Intervalls, dort gilt

$\frac{\mathrm{d}}{\mathrm{d}x}\arcsin x$ $=\frac{1}{\sqrt{1-x^2}}.$

2.3.3. Beispiel.

Der Sinus hyperbolicus $\sinh :\mathbb{R}\to \mathbb{R}$ ist streng monoton wachsend, stetig und weder nach oben noch nach unten beschränkt, also invertierbar.

Die Umkehrfunktion heißt Areasinus hyperbolicus, bezeichnet mit $\mathrm{arsinh}$.

Aus

$(\sinh x{)}^2={\left(\frac{1}{2}({\mathrm{e}}^x-{\mathrm{e}}^{-x\phantom{2}})\right)}^2$ $=\frac{1}{4}({\mathrm{e}}^{2x}-2+{\mathrm{e}}^{-2x})$

$(\cosh x{)}^2={\left(\frac{1}{2}({\mathrm{e}}^x+{\mathrm{e}}^{-x\phantom{2}})\right)}^2$ $=\frac{1}{4}({\mathrm{e}}^{2x}+2+{\mathrm{e}}^{-2x})$

ergibt sich die Beziehung $(\cosh x{)}^2-(\sinh x{)}^2=1$

Damit erhalten wir die Ableitung von $\mathrm{arsinh}$ bei $y_0=\sinh (x_0)$ als

$\frac{\mathrm{d}}{\mathrm{d}y}{\phantom{\frac{0}{0}}\mathrm{arsinh}y|}_{y=y_0}$ $=\frac{1}{{\sinh }^{\prime }{x}_0^{}}$ $=\frac{1}{\cosh x_0^{}}$ $=\frac{1}{\sqrt{1+(\sinh x_0^{}{)}^2}}$ $=\frac{1}{\sqrt{1+y_0^2}}$.

Wir haben damit eingesehen:

${\mathrm{arsinh}}^{\prime }x=\frac{1}{\sqrt{1+x^2}}$

Mit analogen Methoden zeigt man:

2.3.4. Beispiele.

Für die Umkehrfunktion $\arctan :\mathbb{R}\to (-\frac{\pi }{2},\frac{\pi }{2})$ von $\tan :(-\frac{\pi }{2},\frac{\pi }{2})\to \mathbb{R}$ gilt ${\arctan }^{\prime }x=\frac{1}{1+x^2}$.

Die Umkehrfunktion $\ln :{\mathbb{R}}^{+}\to \mathbb{R}$ der Exponentialfunktion $\exp :\mathbb{R}\to {\mathbb{R}}^{+}$ hat die Ableitung ${\ln }^{\prime }(x)=\frac{1}{x}$.

Diese Ergebnisse sind sehr wertvoll beim Integrieren.