| ↰ 3.1 | Material | 3.6 → |
| ← 3.4 | HM 2 | 4.1 ↳ |
Es sei \( [a,b] \) ein Intervall und \( P=\{x_0^{},\ldots,x_n^{}\} \) eine Partition dieses Intervalls:
Es gelte also \( a=x_0^{} \lt x_1^{} \lt \cdots \lt x_n^{} = b \).
Für jede beschränkte Funktion \( f\colon [a,b]\to\RR \) setzen wir
\( \alert{I_k} := \inf\bigset{f(x)}{x\in[x_{k-1}^{},x_k]} \),
\( \alert{S_k} := \sup\bigset{f(x)}{x\in[x_{k-1}^{},x_k]} \).
Dann heißt
\( \alert{\unterS(f,P)} \) \( := \ds\sum_{k=1}^n I_k\cdot(x_k^{}-x_{k-1}^{}) \) Untersumme von \(f\) zur Partition \(P\), und
\( \alert{\oberS(f,P)} \) \( := \ds\sum_{k=1}^n S_k\cdot(x_k^{}-x_{k-1}^{}) \) heißt Obersumme von \(f\) zur Partition \(P\).
Für eine stetige Funktion \(f\) mit \( f(x)\ge0 \) für alle \( x\in[a,b] \) gilt für die Fläche \(F\) zwischen der \(x\)-Achse und dem Graph von \(f\):
\( \unterS(f,P) \le F \le \oberS(f,P) \).
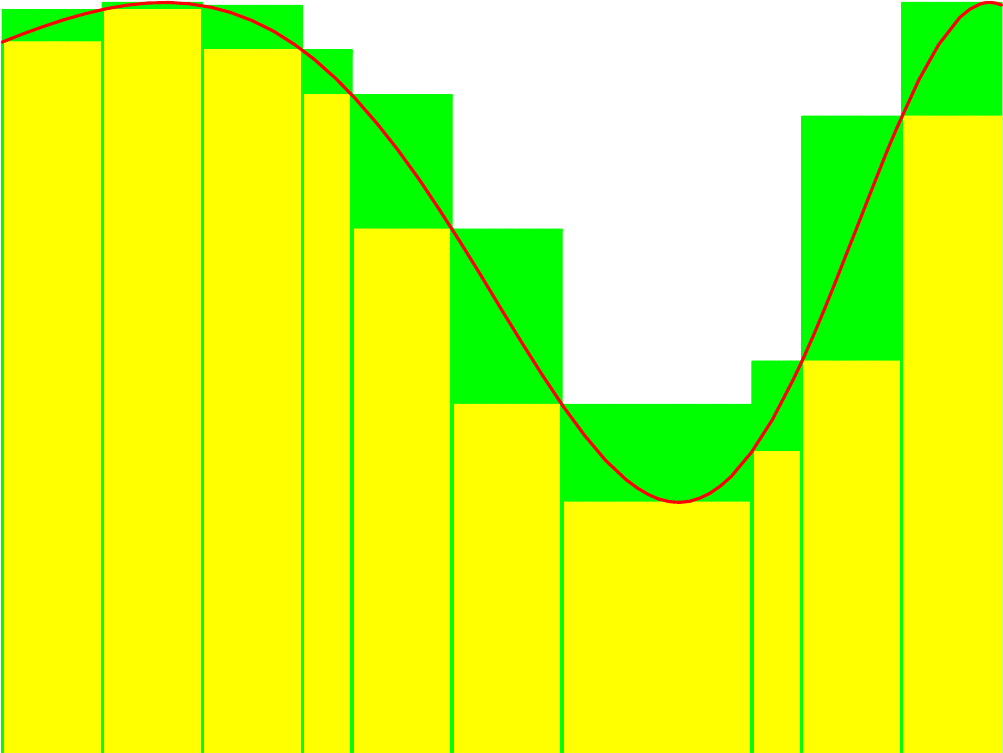
In der folgenden Skizze sehen Sie eine Ober- und eine Untersumme für die Funktion \( f\colon\, [1,13] \to \RR \colon x \mapsto \frac{4\,\sin(x)}{x^2} +2 \).
Die Teilungspunkte der dabei benutzten Partition \( P = \{x_0, x_1, \dots, x_7\} \) des Definitionsintervalls können Sie interaktiv verändern; dabei ändern sich die Ober- und Untersumme mit.
Je nach Funktion \(f\) und benutzter Partition \(P\) ist der Unterschied zwischen Unter- und Obersumme beträchtlich.
Man versucht, diesen Unterschied durch Verfeinern der Partition zu verkleinern:
Eine Partition \( Q =\{y_0^{},\ldots,y_\ell^{}\} \) eines Intervalls heißt Verfeinerung der Partition \( P=\{x_0^{},\ldots,x_n^{}\} \) desselben Intervalls, wenn \( P\subseteq Q \) gilt,
wenn also jeder Teilungspunkt in \(P\) auch einer in \(Q\) ist.
Die Feinheit der Partition \(P\) ist \( \alert{\max\set{x_k^{}-x_{k-1}^{}}{1\le k\le n}} \).
Wir hoffen, dass \( \unterS(f,P) \) und \( \oberS(f,P) \) gegen das Maß der Fläche \(F\) konvergieren, wenn die Feinheit von \(P\) gegen \(0\) strebt.
Bei diesen Überlegungen gehen wir aus von einem anschaulichen
Begriff der Fläche
— mathematisch exakt wird die Fläche eben als Grenzwert der Unter-
und Obersummen definiert!
Um die Konvergenz gegen die Fläche zu sichern,
betrachtet man die Annäherung von unten und von oben:
wenn beide Wege zum selben Grenzwert führen, nennen wir diesen die Fläche.
Die Konvergenz der Unter- und Obersummen wird jeweils gesichert durch:
Sei \( f\colon[a,b]\to\RR \) eine beschränkte Funktion, und seien \(P\) und \(Q\) Partitionen des Intervalls \( [a,b] \).
Bei Verfeinerung der Partition wachsen also die Untersummen und fallen die Obersummen, während sie sich gegenseitig beschränken:
Nach dem Satz von Bolzano und Weierstraß 1.6.5 konvergieren beide.
Für jede beschränkte Funktion \( f\colon[a,b]\to\RR \) setzen wir
\( \alert{\unterS} := \) \( \sup\bigset{\unterS(f,P)}{P\text{ Partition von }[a,b]} \),
\( \alert{\oberS} := \) \( \inf\bigset{\oberS(f,P)}{P\text{ Partition von }[a,b]} \).
Man nennt \(f\) Riemann-integrierbar, wenn \( \alert{\unterS=\oberS} \) gilt.
In diesem Fall heißt der Wert \( \unterS \) das Riemann-Integral über \(f\) von \(a\) bis \(b\).
Das Riemann-Integral ist eine reelle Zahl.
Man schreibt dann auch \( \ds \int\limits_a^b f(x) \,\diff x \) für diesen Wert.
Dass wir dieselbe Schreibweise wie beim bestimmten Integral benutzen,
lässt sich natürlich nur rechtfertigen, wenn die verschiedenen
Definitionen dasselbe liefern:
Dies sichert der Hauptsatz der Differential- und Integralrechnung
3.6.3.
Es sei \( f\colon[a,b]\to\RR \) eine Funktion.
[Die Beschränktheit folgt nach Weierstraß 1.13.12.]
Etwas allgemeiner gilt:
Wir definieren die Funktion
\( q\colon[0,1]\to\RR\colon{} x\mapsto \begin{cases} 1 & \text{ falls $x\in\QQ$, }\\ 0 & \text{ sonst.} \end{cases} \)
Diese Funktion ist nicht Riemann-integrierbar.
Die Funktionen \( f,g\colon [a,b]\to\RR \) seien Riemann-integrierbar.
\( \int\limits_a^b\bigl(\alpha\,f(x)+\beta\,g(x)\bigr)\,\diff x \) \( = \alpha\,\int\limits_a^b f(x)\,\diff x + \beta\,\int\limits_a^b g(x)\,\diff x \,. \)
\( \int\limits_a^b f(x) \,\diff x \le \int\limits_a^b g(x) \,\diff x \).
\( \left|\int\limits_a^b f(x)\,\diff x\right| \le \int\limits_a^b \left|f(x)\right|\,\diff x \)
(Integral-Variante der Dreiecksungleichung).
Die positive untere Schranke an \(|g|\) brauchen wir, damit der Quotient \(f/g\) beschränkt bleibt.
Für jede Riemann-integrierbare Funktion \( f\colon[a,b]\to\RR \) und jede Stelle \( z\in(a,b) \) sind auch die Einschränkungen von \(f\) auf die Intervalle \( [a,z] \) und \( [z,b] \) Riemann-integrierbar, und es gilt
\( \int\limits_a^b f(x)\,\diff x \) \( = \int\limits_a^z f(x)\,\diff x + \int\limits_z^b f(x)\,\diff x \).
Die Funktion \(f\) ist damit auf jedem Teilintervall von \( [a,b] \) Riemann-integrierbar.
Neben dem Riemann-Integral gibt es weitere Integralbegriffe wie etwa das Lebesgue-Integral oder das Riemann-Stieltjes-Integral.
Wir beschränken uns hier auf Riemann-Integrale und werden fortan
statt Riemann-integrierbar
einfach nur integrierbar
sagen.
| ↰ 3.1 | Material | 3.6 → |
| ← 3.4 | HM 2 | 4.1 ↳ |