1.13. Eigenschaften stetiger Funktionen

Bevor wir uns genauer mit stetigen Funktionen befassen, verabreden wir einige Schreibweisen:

1.13.1. Definition.

Es seien $a,b\in \mathbb{R}$ mit $a\leqq b$.

1. $[a,b]:=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a\leqq x\leqq b}a\leqq x\leqq b\right\}$ heißt abgeschlossenes Intervall (mit Grenzen $a$ und $b$).
2. $(a,b):=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a<x<b}a<x<b\right\}$ heißt offenes Intervall (die Grenzen $a$ und $b$ gehören nicht zur Menge).

Es gibt auch halb offene Intervalle:

3. $[a,b):=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a\leqq x<b}a\leqq x<b\right\}$ (halb offenes Intervall),
4. $(a,b]:=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a<x\leqq b}a<x\leqq b\right\}$ (halb offenes Intervall),

Bei (halb) offenen Intervallen lässt man auch $\pm \mathrm{\infty }$ als Grenze zu: $(-\mathrm{\infty },b):=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{x<b}x<b\right\}$, $(-\mathrm{\infty },b]:=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{x\leqq b}x\leqq b\right\}$, $(a,+\mathrm{\infty }):=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a<x}a<x\right\}$, $[a,+\mathrm{\infty }):=\left\{x\in \mathbb{R}|\phantom{x\in \mathbb{R}}\phantom{a\leqq x}a\leqq x\right\}$, $(-\mathrm{\infty },+\mathrm{\infty }):=\mathbb{R}$.

Es sei $f:M\to \mathbb{R}$ eine Funktion.

Es stellen sich die folgenden grundsätzlichen Probleme:

1.13.2. Nullstellenproblem.

Gibt es $x\in M$ mit $f(x)=0$ ?

Wenn ja: Wie berechnet / findet man diese Nullstellen?

1.13.3. Lösbarkeitsproblem.

Kann man zu gegebenem $a\in \mathbb{R}$ die Gleichung $f(x)=a$ lösen?

Das Nullstellenproblem ist ein Spezialfall ($a=0$), umgekehrt kann man das allgemeine Lösbarkeitsproblem auf das Nullstellenproblem für die durch $g(x):=f(x)-a$ gegebene Funktion $g:M\to \mathbb{R}$ reduzieren.

1.13.4. Gleichheitsproblem.

Gibt es für zwei Funktionen $f,g:M\to \mathbb{R}$ eine Stelle $x\in M$, an der die beiden denselben Wert annehmen?

Auch dieses Problem kann man reduzieren auf das Nullstellenproblem (für die durch $d(x):=f(x)-g(x)$ gegebene Funktion $d:M\to \mathbb{R}$).

Für beliebige Funktionen ist das Nullstellenproblem sehr schwierig. Anders für stetige Funktionen: Hier gibt es allgemeine (abstrakte) Existenzsätze für Nullstellen, aus denen sich Algorithmen zur Approximation dieser Nullstellen entwickeln lassen. Hat man Existenzsätze (oder Algorithmen) für Nullstellen, so kann man damit auch das allgemeine Lösbarkeitsproblem und das Gleichheitsproblem angehen.

1.13.5. Nullstellensatz von Bolzano.

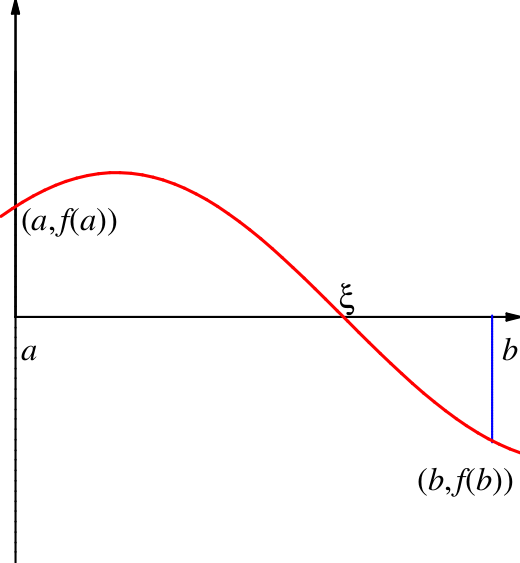
Es sei $f:M\to \mathbb{R}$ stetig, außerdem gelte $f(a)\geqq 0$ und $f(b)\leqq 0$. Dann gibt es $\xi \in [a,b]$ mit $f(\xi )=0$.

Zur Anschauung:

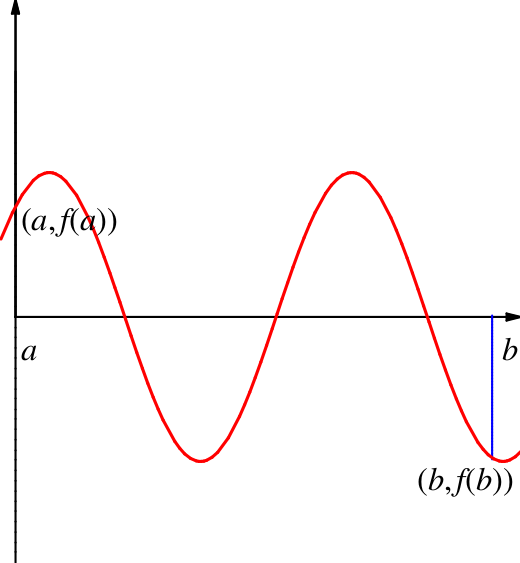
Beim Nullstellensatz von Bolzano ist die Stetigkeit der Funktion wichtig — und genauso die Annahme, dass der Definitionsbereich ein Intervall ist!

Wir erhalten sofort eine Anwendung auf das Lösbarkeitsproblem:

1.13.6. Zwischenwertsatz.

Es sei $f:[a,b]\to \mathbb{R}$ stetig, und es gelte $f(a)\geqq f(b)$. Dann nimmt $f$ jeden Wert zwischen $f(a)$ und $f(b)$ mindestens einmal an.

Mit anderen Worten: Zu jedem $y_0^{}\in [f(b),f(a)]$ gibt es $x_0^{}\in [a,b]$ mit $f(x_0^{})=y_0^{}$.

Eine raffiniertere Anwendung des Nullstellensatzes bzw. des Zwischenwertsatzes auf das Gleichheitsproblem finden Sie hier als interaktive Seite.

Die bequemste Methode, das Lösbarkeitsproblem zu bewältigen, wäre eine Inverse zur Abbildung $f$:

1.13.7. Definition.

Es sei $f:X\to Y$ eine Funktion.

Eine Funktion $g:Y\to X$ heißt Umkehrfunktion von $f$ (bezeichnet mit $g=f^{-1}$ ), wenn gilt:

$\mathrm{\forall }x\in X:g(f(x))=x$ $\wedge \mathrm{\forall }y\in Y:f(g(y))=y$.

Mit anderen Worten: Es gilt $g\circ f=\mathrm{id}{|}_X$ und $f\circ g=\mathrm{id}{|}_Y$.

Warnung:

Man darf die Schreibweise $f^{-1}$ nicht mit $\frac{1}{f}$ verwechseln, das sind völlig verschiedene Dinge!

Eine Umkehrfunktion $f^{-1}$ gibt es genau dann, wenn $f$ bijektiv (also surjektiv und injektiv) ist.

Man kann jede Funktion $f:X\to Y$ surjektiv machen, indem man sie als Funktion von $X$ nach $f(X)$ betrachtet. Die Injektivität ist also der Knackpunkt bei der Frage nach der Existenz einer Umkehrfunktion.

1.13.8. Beispiel.

Die Funktion $f:\mathbb{R}\to \mathbb{R}:x\mapsto x^2$ ist weder injektiv noch surjektiv, liefert aber eine surjektive Funktion von $\mathbb{R}$ nach $f(\mathbb{R})=[0,+\mathrm{\infty })$.

Durch geeignete Einschränkungen erhält man bijektive Funktionen:

Die Umkehrfunktion zu $g:[0,+\mathrm{\infty })\to [0,+\mathrm{\infty }):x\mapsto x^2$ ist $g^{-1}:[0,+\mathrm{\infty })\to [0,+\mathrm{\infty }):x\mapsto \sqrt{x}$.

Die Umkehrfunktion zu $h:(-\mathrm{\infty },0]\to [0,+\mathrm{\infty }):x\mapsto x^2$ ist $h^{-1}:[0,+\mathrm{\infty })\to (-\mathrm{\infty },0]:x\mapsto -\sqrt{x}$.

1.13.9. Beispiel.

Die injektive Funktion $f:\mathbb{R}\to \mathbb{R}:x\mapsto {\mathrm{e}}^x$ ist nicht surjektiv, wir erhalten aber eine bijektive Funktion $\exp :\mathbb{R}\to (0,+\mathrm{\infty }):x\mapsto {\mathrm{e}}^x$ mit Umkehrfunktion $\ln :(0,+\mathrm{\infty })\to \mathbb{R}:x\mapsto \ln x$.

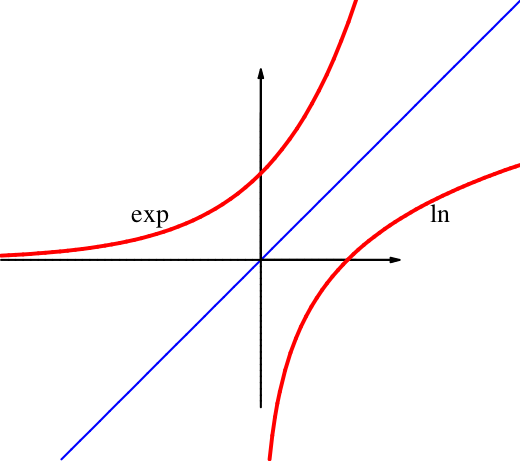
Generell gilt: Wenn die Umkehrfunktion $f^{-1}$ existiert, erhält man deren Graph durch Spiegelung des Graphen von $f$ an der ersten Winkelhalbierenden.

1.13.10. Beispiel.

Die Funktion $f:\mathbb{R}\to \mathbb{R}:x\mapsto x^3$ ist bijektiv.

Um die Injektivität einzusehen, betrachten wir $x_1,x_2\in \mathbb{R}$ mit $x_1\ne x_2$: Wir können etwa $x_1<x_2$ annehmen.

Dann gilt auch $f(x_1)=x_1^3<x_2^3=f(x_2)$; insbesondere also $f(x_1)\ne f(x_2)$.

Die Surjektivität folgt aus dem Zwischenwertsatz:

Man muss sich nur klar machen, dass es zu jeder reellen Zahl $y$ Zahlen $x_1^{},x_2^{}\in \mathbb{R}$ mit $x_1^3\leqq y\leqq x_2^3$ gibt.

Wegen $\underset{n\to \mathrm{\infty }}{lim}{n}^3=+\mathrm{\infty }$ kann man sogar $x_1^{},x_2^{}\in \mathbb{Z}$ finden.

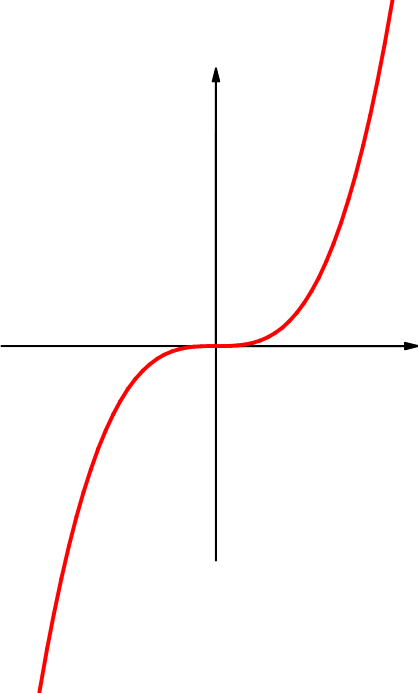
Wir verallgemeinern:

1.13.11. Satz.

Es sei $f:[a,b]\to \mathbb{R}$ stetig. Dann ist $f$ genau dann injektiv, wenn $f$ streng monoton (steigend oder fallend) ist.

In diesem Fall liefert $f$ eine Bijektion von $[a,b]$ auf $f([a,b])$, und es gilt $f([a,b])=[f(a),f(b)]$ bzw. $f([a,b])=[f(b),f(a)]$ — je nachdem, ob $f$ steigt oder fällt.

1.13.12. Weierstraßscher Satz vom Minimum und Maximum.

Ist $f:[a,b]\to \mathbb{R}$ stetig, so nimmt $f$ auf dem Intervall ein Minimum und ein Maximum an:

Es gibt ${\xi }_1,{\xi }_2\in [a,b]$ so, dass $\mathrm{\forall }x\in [a,b]:$ $f({\xi }_1)\leqq f(x)\leqq f({\xi }_2)$,

Aus dem Nullstellensatz von Bolzano (1.13.5) ergibt sich die folgende Methode zur Nullstellenbestimmung: