| ↰ 1.1 | Material | 1.3 → |
| ← 1.1 | HM 2 | 2.1 ↳ |
Eine Folge \((a_n)_{n\in\NN}\) reeller Zahlen heißt
Eine Folge \((a_n)_{n\in\NN}\) reeller Zahlen heißt
Wenn eine Folge gleichzeitig monoton steigend und fallend ist, sind alle ihre Folgenglieder gleich: solche Folgen heißen konstant.
Die durch \(a_n:=\frac1n\) gegebene Folge \((a_n)_{n\in\NN}\) ist streng monoton fallend.
Sie ist nach oben beschränkt [z.B. durch \(S=1\) oder auch durch \(S=178\)].
Die Folge ist auch nach unten beschränkt [z.B. durch \(s=0\) oder \(s=-3295\)].
Die schon in 1.1.4 betrachtete alternierende Folge \((a_n)_{n\in\NN}\) mit \(a_n=(-1)^n\) ist beschränkt [z.B. durch \(S=1\) und \(s=-1\)], aber nicht monoton.
Die Folge \((b_n)_{n\in\NN}\) aus 1.1.6 ist nach unten beschränkt [mit \(s=0\)], und monoton steigend.
Allerdings ist sie wegen \(b_2=1=b_3\) nicht streng monoton steigend.
In der Zinseszinsrechnung, allgemeiner zur Beschreibung gewisser Formen des Wachstums, braucht man Folgen wie die durch \(a_n:=\bigl(1+\frac1n)^n\) definierte.
Diese Folge ist jedenfalls nach unten beschränkt [etwa durch \(1\)].
Wir wollen klären, ob die Folge monoton steigend ist.
Zunächst betrachten wir die ersten Glieder:
\( \renewcommand{\arraystretch}{1.2}% \begin{array}{rcccl} a_1 & = & 2 \\ % a_2 & = & \ds\frac{9}{4} & = & 2,25 \\ % a_3 & = & \ds\frac{64}{27} & \approx & 2,37\ldots \\ % a_4 & = & \ds\frac{625}{256} & \approx & 2,44\ldots \\ % a_5 & = & \ds\frac{7776}{3125} & \approx & 2,48\ldots \\ % a_6 & = & \ds\frac{117649}{46656} & \approx & 2,52\ldots \\ % a_7 & = & \ds\frac{2097152}{823543} & \approx & 2,54\ldots \\ % \end{array} \)
Die Folge \((a_n)_{n\in\NN}\) mit \(a_n:=\bigl(1+\frac1n\bigr)^n\) ist beschränkt und streng monoton wachsend.
Wir zeigen zuerst
\( (*)\qquad \forall\, n\ge2\colon{} \quad a_n \lt \sum_{k=0}^n \frac1{k!} \,. \)
Danach werden wir zeigen:
\( (**)\qquad \forall\, n\ge2\colon{} \quad \sum_{k=0}^n \frac1{k!} \le 3 \,. \)
\( \renewcommand{\arraystretch}{2.2} \begin{array}{rclcl} a_n & = & \ds \left(1+\frac1n\right)^n \\ & = & \ds \sum_{k=0}^n \binom nk\, \frac1{n^k} \\ & = & \ds 1 + \sum_{k=1}^n \binom nk\, \frac1{n^k} \\ & = & \ds 1 + \sum_{k=1}^n \frac{n\,(n-1)\,\cdots(n-k+1)}{k!}\cdot\frac1{n^k} \\ & = & \ds 1 + \sum_{k=1}^n \frac1{k!} \cdot \frac nn\cdot\frac{n-1}n\cdots\cdot\frac{n-k+1}n \\ & = & \ds 1 + \sum_{k=1}^n \frac1{k!} \underbrace{\left(1-\frac1n\right)\cdots\left(1-\frac{k-1}n\right)}_{{}\lt1} & \lt & \ds 1 + \sum_{k=1}^n \frac1{k!} = \sum_{k=0}^n \frac1{k!} \,. \end{array} \)
Durch den Vergleich
\( \begin{array}[t]{rcccccccc} k! & {}={} & k & \cdot & (k-1) & \cdots & 2 & \cdot & 1 \\ 2^{k-1} & {}={} & 2 & \cdot & 2 & \cdots & 2 & \cdot & 1 \end{array} \)
erhalten wir für alle \(k\in\NN\) die Ungleichung \(2^{k-1} \le k!\) und daraus
\( \forall\,k\in\NN\colon{} \dfrac1{k!} \le \dfrac1{2^{k-1}} \,. \)
Jetzt ergibt sich
\(\renewcommand{\arraystretch}{2} \begin{array}{rclcl}\ds \sum_{k=0}^n \frac1{k!} = 1 + 1 + \sum_{k=2}^n \frac1{k!} & = & \ds 2 + \sum_{k=2}^n \frac1{k!} \\ &\le& \ds 2 + \sum_{k=2}^n \frac1{2^{k-1}} \\ & = & \ds 2 + \frac12\,\sum_{k=2}^n \frac1{2^{k-2}} \\ & = & \ds 2 + \frac12\,\sum_{\ell=0}^{n-2} \frac1{2^{\ell}} \\ & = & {\ds 2 + \frac12\left(1+\frac12+\frac14+\frac18+\cdots +\frac1{2^{n-2}}\right) % {}\le 2 + 1 =3\,.} \end{array} \)
Die letzte Ungleichung benutzt \( \sum_{\ell=0}^m \frac1{2^\ell} \le 2 \,. \)
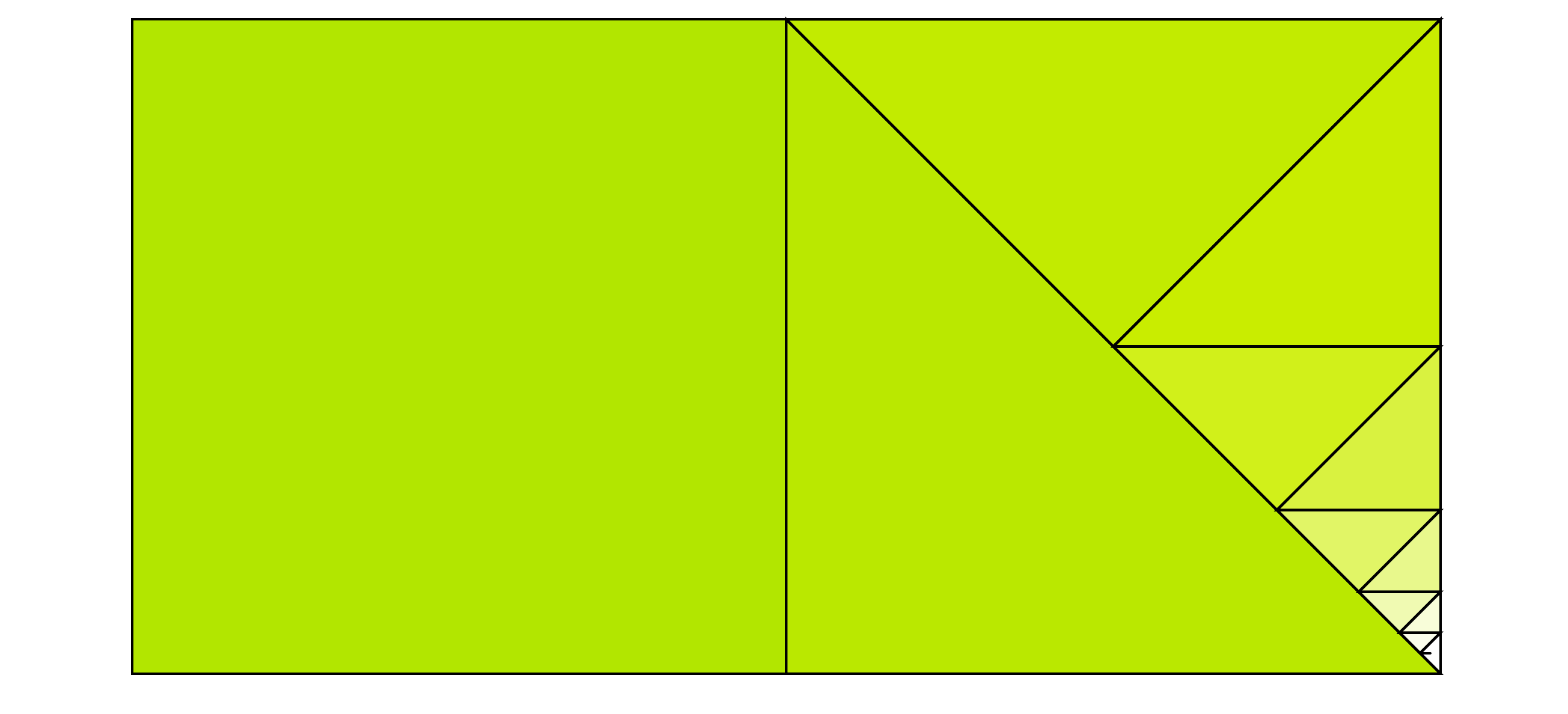
Man kann diese Abschätzung durch Induktion begründen, wir geben hier einen geometrischen (und damit anschaulichen) Beweis:

Man startet mit dem Quadrat vom Inhalt \(1=\frac1{2^0}\) und fügt danach durch sukzessive Halbierung gewonnene Dreiecke an.
Jedes neue Dreieck ist halb so groß wie das vorhergehende, das \(\ell\)-te Dreieck hat also den Inhalt \(\frac1{2^\ell}\).
Die Summe \(\sum_{\ell=0}^m\frac1{2^\ell}\) beschreibt den Inhalt des Quadrats zusammen mit den ersten \(m\) Dreiecken: das ist offenbar weniger als der Inhalt der beiden Quadrate!
Wir haben jetzt mit 1.2.7, \((*)\) und \((**)\) nachgewiesen, dass unsere Folge beschränkt ist.
Es bleibt die Monotonie zu zeigen, also \(\forall\,n\in\NN\colon a_{n+1}-a_n>0\).
Wir benutzen wieder wie oben die Beziehung \(a_n= 1 + \sum_{k=1}^n \frac1{k!}\,\left(1-\frac1n\right)\cdots\left(1-\frac{k-1}n\right)\), und erhalten
\( \begin{array}{rcc} \blau{a_{n+1}}-\red{a_n} & = & \blau{\ds 1 + \sum_{k=1}^{n+1} \frac1{k!}\left(1-\frac1{n+1}\right)\cdots\left(1-\frac{k-1}{n+1}\right)} \\ && \red{\ds - 1 - \sum_{k=1}^n\frac1{k!}\left(1-\frac1n\right)\cdots\left(1-\frac{k-1}n\right)} \\ & = & \gruen{\ds \frac1{(n+1)!}\,\left(1-\frac1{n+1}\right)\cdots\left(1-\frac{n}{n+1}\right)} \\ && \blau{+ \ds\sum_{k=1}^n \frac1{k!}\,\left(1-\frac1{n+1}\right)\cdots\left(1-\frac{k-1}{n+1}\right) } \\ && \red{\ds - \sum_{k=1}^n \frac1{k!}\,\left(1-\frac1{n}\right)\cdots\left(1-\frac{k-1}{n}\right)} \,. \end{array} \)
Für alle \(n\in\NN\) und alle \(x>0\) gilt
\( \frac1n>\frac1{n+1} \,,\quad \frac xn>\frac x{n+1} \quad \text{ und damit }\quad 1 - \frac x{n+1} > 1 - \frac xn \,. \)
Wir wenden dies speziell für \(x\in\{1,\ldots,k-1\}\) an, und erhalten
\( \blau{\left(1-\frac1{n+1}\right)\cdots\left(1-\frac{k-1}{n+1}\right)} - \red{\left(1-\frac1{n}\right)\cdots\left(1-\frac{k-1}{n}\right)} > 0 \,. \)
Nach Multiplikation mit \(\frac1{k!}\), Summation über \(k\) und wegen
\( \gruen{\frac1{(n+1)!}\,\left(1-\frac1{n+1}\right)\cdots\left(1-\frac{n}{n+1}\right)} > 0 \)
liefert dies die Behauptung: \(\blau{a_{n+1}}-\red{a_n}>0\).
Damit ist unsere Folge auch als streng monoton steigend erkannt.
Später (in 1.6.5) werden wir sehen, dass jede monotone beschränkte Folge reeller Zahlen gegen einen wohlbestimmten reellen Grenzwert strebt.
Dem Grenzwert der eben betrachteten Folge geben wir einen besonderen Namen:
Der Grenzwert der Folge \(\left(\bigl(1+\frac1n\bigr)^n\right)_{n\in\NN}\) heißt Eulersche Zahl und wird mit \(\alert\E\) bezeichnet.
Näherungsweise gilt \( \E \approx 2,718281828\ldots \)
Entgegen dem ersten Eindruck ist die Dezimalentwicklung nicht periodisch!
In der Tat kann man die Eulersche Zahl nicht elementarer (etwa als Bruch, oder als Nullstelle eines Polynoms) definieren — einfacher als über unsere einigermaßen verwickelte Definition ist diese Zahl nicht zu haben.
| ↰ 1.1 | Material | 1.3 → |
| ← 1.1 | HM 2 | 2.1 ↳ |