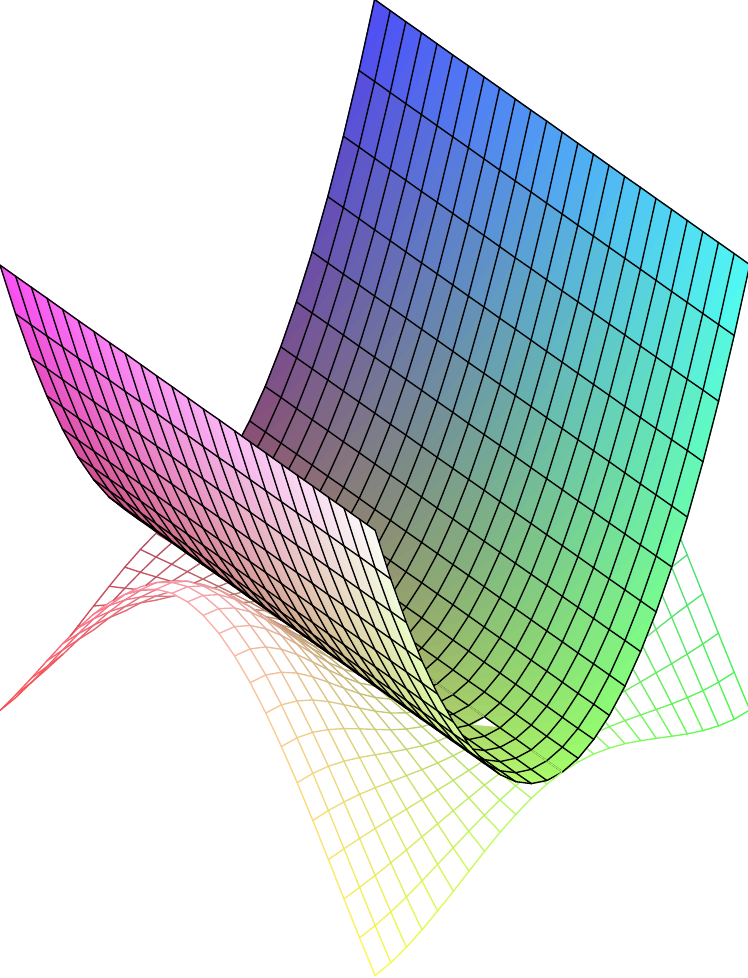
\(f\binom xy=x\,\sin x\,\cos y\),
Schmiegquadrik an der Stelle \(\binom00\): \(z=x^2\)
| ↰ 4.1 | Material | 4.5 → |
| ← 4.3 | HM 2 | 5.1 ↳ |
Die Taylorformel 2.6.1 haben wir in der eindimensionalen Analysis benutzt, um Funktionen durch affin lineare Funktionen oder Polynome von höherem Grad zu approximieren.
Wir wollen dies auch für Funktionen mehrerer Veränderlicher tun.
Zur Beschreibung der Approximationsqualität benutzen wir den folgenden Begriff:
Es sei \( D\subseteq\RR^n \) und \( a\in\inn D \).
Außerdem sei \( k\in\NN \).
Für Funktionen \(f\) und \(g\) von \(D\) nach \(R^\ell\) schreibt man
\( f(x) = g(x) + \alert{o\left(\vert x-a\vert^k\right)} \),
wenn
⚽ \(\quad \alert{\lim\limits_{x\to a}\frac{\vert f(x)-g(x)\vert}{\vert x-a\vert^k} =0 } \)
gilt.
Das eben eingeführte Symbol klein o
ist eines der
Landau-Symbole.
Ist ⚽ mit \(k = 1\) erfüllt, so sagt man, die Funktion \(g\) approximiert \(f\) linear (an der Stelle \(a\)).
Im Fall \(k = 2\) spricht man von quadratischer Approximation.
Je höher \(k\) in ⚽
gewählt werden kann, desto besser ist die
Approximation.
Für Details sei auch hier auf die Numerik verwiesen.
Es sei \( D\subseteq\RR \) ein offenes Intervall und \(f \colon D \to \RR\) eine Funktion (einer Veränderlicher).
Ist \(a\in D\) und \(f\) zweimal stetig differenzierbar an der Stelle \(a\), so gilt
\( f(x) \) \( = f(a) + f'(a)(x-a) + o(|x-a|^{\alert{1}}) \).
Nach dem Satz von Taylor 2.6.1 gilt
\( \frac{f(x)-f(a)-f'(a)(x-a)}{|x-a|} \) \( = \frac{f(x)-T_1(f,x,a)}{|x-a|} \) \( = \frac{R_1(f,x,a)}{|x-a|} \) \( = \frac{f''\left(a+\vartheta\,(x-a)\right)(x-a)^2}{2\,|x-a|} \) \( \konv[x\to a]\quad 0 \).
Im eben betrachteten Beispiel dient die Annahme \( f\in\Cf2D \) nur der Bequemlichkeit:
Die Aussage \( f(x) \) \( = \) \( T_1(f,x,a)+o(|x-a|) \) bleibt auch richtig, wenn wir nur einfache Differenzierbarkeit voraussetzen.
Wir drehen den Spieß um und erheben die lineare Approximierbarkeit zur allgemeinen Definition von Differenzierbarkeit:
Sei \( D\subseteq\RR^n \) offen, und sei \( a\in D \).
Eine Funktion \( f\colon D\to\RR \) heißt (total) differenzierbar an der Stelle \(a\), wenn es einen Vektor \( v(a)\in\RR^n \) derart gibt, dass gilt:
\( f(x) \) \( = f(a) + v(a)\skalp(x-a) \alert{{}+ o\left(\vert x-a\vert\right)} \).
Der Vektor \(v (a)\) heißt dann die totale Ableitung von \(f\)
an der Stelle \(a\) (oder kürzer in \(a\)
).
Es sei \( D\subseteq\RR^n \) offen, und es sei \( f\in\Cf1D \).
Dann ist \(f\) an jeder Stelle \( a\in D \) total differenzierbar, wobei
\( \alert{v(a)=\grad f(a)} \):
\( f(x) \) \( = f(a) + \grad f(a)\skalp(x-a) \) \( + o\left(\vert x-a\vert\right) \).
Umgekehrt gilt: Ist \(f\) an der Stelle \(a\) total differenzierbar, so existieren alle partiellen Ableitungen, und es gilt \( \alert{\grad f(a)=v(a)} \).
In der eindimensionalen Analysis liefert die Taylorformel auch Approximationen höheren Grades.
Um die Taylorformel auch für Funktionen mehrerer Veränderlicher formulieren zu können, brauchen wir weitere Begriffe und Schreibweisen:
Eine Teilmenge \( D\subseteq\RR^n \) heißt konvex, wenn zu je zwei Punkten \(a , b \in D\) die gesamte Verbindungsstrecke \( \overline{a\,b} \) in \(D\) enthalten ist.
Die folgende Darstellung zeigt eine (vermutlich) konvexe Menge links und eine definitiv nicht konvexe Menge rechts.
Zur Veranschaulichung des Problems bei der Vereinigung konvexer Mengen gibt es ein kleines kühles Video.
Es sei \( j\in\NN \). Die Menge \( \Cf jD \) bildet (mit den üblichen, werteweisen Verknüpfungen) einen reellen Vektorraum.
Für \( f\in\Cf jD \) und \( v\in\RR^n\setminus\{0\} \) gehört \( \partial_v^{}\,f\colon D\to\RR\colon{} \) \( x\mapsto \partial_v^{}\,f(x) \) zu \( \Cf{j-1}D \).
Wir können also \( \partial_v^{} \) auffassen als eine Abbildung von \( \Cf jD \) nach \( \Cf{j-1}D \).
Diese Abbildung ist linear!
Wir schreiben \( \alert{\partial_v^{\,k}} \) für die \(k\)-fache Anwendung von \( \partial_v^{} \):
Das ist dann eine lineare Abbildung von \( \Cf jD \) nach \( \Cf{j-k}D \).
Wir wollen \( \partial_v^{\,2}\,f(a) \) noch etwas expliziter bestimmen.
Wir schreiben für den Moment (vgl. 4.3.12)
\( g(x):=\partial_v^{}\,f(x) \) \( = v\skalp\grad f(x) \) \( = \sum\limits_{j=1}^n v_j\,f_{x_j}^{}(x) \):
Dann gilt
\( \partial_v^{\,2}\,f(a) \) \( = \partial_v^{}\,g(a) \) \( = \left( \begin{array}{c} g_{x_1}^{}(a) \\ \vdots\\ g_{x_n}^{}(a) \end{array} \right) \skalp v \) \( = \left( \begin{array}{c} \color{blue}{\bigl(}\sum_{j=1}^n v_j^{}\,f_{x_j}^{}\color{blue}{\bigr)}\vphantom{f}_{x_1}^{}(a) \\ \vdots\\\pause \color{blue}{\bigl(}\sum_{j=1}^n v_j^{}\,f_{x_j}^{}\color{blue}{\bigr)}\vphantom{f}_{x_n}^{}(a) \end{array} \right) \skalp v \) \( = \left( \begin{array}{c} \sum_{j=1}^n v_j^{}\,f_{x_j\,x_1}^{}(a) \\ \vdots\\ \sum_{j=1}^n v_j^{}\,f_{x_j\,x_n}^{}(a) \end{array} \right) \skalp v \) \( = \sum\limits_{k=1}^n \left(\sum\limits_{j=1}^n v_j^{}\,f_{x_j\,x_k}^{}(a)\right)\,v_k^{} \)
Dies können wir interpretieren als Matrixprodukt:
\( \partial_v^{\,2}\,f(a) \) \( = v\transp \,\left( \begin{array}{ccc} f_{x_1^{}\,x_1^{}}^{}(a) & \cdots & f_{x_1^{}\,x_n^{}}^{}(a) \\ \vdots & & \vdots \\ f_{x_n^{}\,x_1^{}}^{}(a) & \cdots & f_{x_n^{}\,x_n^{}}^{}(a) \end{array} \right) \, v \,. \)
Nachdem wir im Rahmen der Analysis
bisher eher lax mit der Frage umgegangen sind, ob die Elemente des \(\RR^n\)
als Zeilen oder Spalten aufzufassen sind, müssen wir jetzt Farbe
bekennen:
Wie in den einschlägigen Teilen der Linearen Algebra wollen wir eigentlich mit
Spalten rechnen, der linke Faktor im Matrixprodukt muss aber eine Zeile
sein. Deswegen muss dort \(v\) transponiert werden.
Es sei \(a\in D\) und \( D\subseteq\RR^n \) sowie \( f\in\Cf2D \).
Die Matrix
\( \alert{\Hesse fa} := \) \( \left(\pause \begin{array}{ccc} f_{x_1^{}\,x_1^{}}(a) & \cdots & f_{x_1^{}\,x_n^{}}(a) \\ \vdots && \vdots \\ f_{x_n^{}\,x_1^{}}(a) & \cdots & f_{x_n^{}\,x_n^{}}(a) \end{array} \right) \)
nennt man die Hesse-Matrix von \(f\) an der Stelle \(a\).
Wir haben vorausgesetzt, dass \(f\) zweimal stetig partiell differenzierbar ist.
Nach dem Satz von Schwarz 4.3.10 ist die Hesse-Matrix \( \Hesse fa \) symmetrisch.
Diese symmetrische Matrix ist die angemessene Beschreibung der quadratischen Form \( v\mapsto \partial_v^{\,2}\,f(a) \).
Wenn man die Überlegungen aus 4.4.9 iteriert, erhält man
\( \partial_v^{\,3}\,f(a) \) \( = \sum\limits_{\ell=1}^n \sum\limits_{k=1}^n \sum\limits_{j=1}^n f_{x_j\,x_k\,x_\ell}^{}(a)\,v_j^{}v_k^{}v_\ell^{} \)
\( \partial_v^{\,4}\,f(a) \) \( = \sum\limits_{m=1}^n \sum\limits_{\ell=1}^n \sum\limits_{k=1}^n \sum\limits_{j=1}^n f_{x_j\,x_k\,x_\ell\,x_m}^{}(a)\,v_j^{}v_k^{}v_\ell^{}v_m^{} \)
Es sei \( D\subseteq\RR^n \) konvex und offen. Weiter sei \( f\in\Cf{k+1}D \) und \( a\in D \).
Dann gilt für alle \( v\in\RR^n \), die \( a+v\in D \) erfüllen:
\( f(a+v) \) \( = f(a) + \partial_v^{}\,f(a) \) \( + \frac1{2!} \, \partial_v^{\,2}\,f(a) \) \( + \cdots + \frac1{k!} \, \partial_v^{\,k}\,f(a) \) \( + R_k^{}(a,v) \)
wobei das Restglied sich schreiben lässt als \( \alert{R_k^{}(a,v)} \) \( = \frac1{(k+1)!}\,\partial_v^{k+1}\,f(a+\vartheta\,v) \)
mit geeignetem \( \vartheta\in[0,1] \).
Man nennt
\( \alert{T_k^{}(f,x,a)} \) \( := f(x)-R_k^{}(a,x-a) \) \( = f(a) + \partial_{x-a}^{}\,f(a) + \) \( \frac12\,\partial_{x-a}^{\,2}\,f(a) \) \( + \cdots + \frac1{k!}\,\partial_{x-a}^{\,k}\,f(a) \)
das Taylorpolynom der Stufe \(k\) von \(f\) um \(a\).
Es ist wahr, dass \( T_k^{}(f,x,a) \) ein Polynom in den Veränderlichen \( x_1^{}\color{blue}{-a_1^{}}\), \(x_2^{}\color{blue}{-a_2^{}}\), \(\dots , x_n^{}\color{blue}{-a_n^{}} \) ist.
Für \(k = 3\) sieht man das, indem man 4.4.9 iteriert.
Das Taylorpolynom der Stufe \(1\) ist gerade die lineare Approximation:
\( T_1(f,x,a) \) \( = f(a) + \partial_{x-a}\,f(a) \) \( = f(a) + (x-a)\skalp\grad f(a) \).
Das Taylorpolynom der Stufe \(2\) ergibt sich mit Hilfe der Hesse-Matrix \( \Hesse{f}{a} \) als
\( T_2(f,x,a) \) \( = f(a) +{} \partial_{x-a}\,f(a) + \frac12\,\color{blue}{\partial_{x-a}^{\,2}\,f(a)} \)
\( = f(a) +{} (x-a)\skalp\grad f(a) \) \( + \frac12\,\color{blue}{(x-a)\transp\,\Hesse{f}{a}(x-a)} \).
Mit anderen Worten: Der Graph von \( T_1(f,x,a) \) ist ein affiner Teilraum, der den Graphen von \(f\) an der Stelle \(a\) linear approximiert.
Bei einer Funktion in zwei Variablen ist der Graph von \( T_1\bigl(f,\binom{x_1^{}}{x_2^{}},\binom{a_1^{}}{a_2^{}}\bigr) \) also die Tangentialebene im Punkt \( (a_1,a_2,f(a))\transp = \left(\begin{array}{c}a_1\\a_2\\f(a)\end{array}\right) \) an den Graphen von \(f\):
Diese Tangentialebene hat die Gleichung \( \alert{x_3^{}=T_1\bigl(f,\binom{x_1^{}}{x_2^{}},\binom{a_1^{}}{a_2^{}}\bigr)} \).
Das Taylorpolynom der Stufe \(2\) beschreibt eine Approximation des Graphen von \(f\) durch eine Quadrik:
Es sei \( D\subseteq\RR^2 \) und \( f\in\Cf3D \).
Als Taylorpolynom der Stufe \(2\) an der Stelle \( a=\binom{a_1^{}}{a_2^{}} \) ergibt sich
\( T_2(f,x,a) \) \( = T_2\bigl(f,\binom{x_1^{}}{x_2^{}},\binom{a_1^{}}{a_2^{}}\bigr) \)
\( = f\binom{a_1^{}}{a_2^{}} \) \( + (x_1^{}-a_1^{})\,f_{x_1^{}}\binom{a_1^{}}{a_2^{}} + (x_2^{}-a_2^{})\,f_{x_2^{}}\binom{a_1^{}}{a_2^{}} \)
\( + \frac12\,(x_1^{}-a_1^{})^2\,f_{x_1^{}\,x_1^{}}\binom{a_1^{}}{a_2^{}} \) \( + (x_1^{}-a_1^{})\,(x_2-a_2^{})\,f_{x_1^{}\,x_2^{}}\binom{a_1^{}}{a_2^{}} \) \( + \frac12\,(x_2^{}-a_2^{})^2\,f_{x_2^{}\,x_2^{}}\binom{a_1^{}}{a_2^{}} \)
In \( \RR^3 \) wird durch die Gleichung \( x_3^{} = T_2\bigl(f,\binom{x_1^{}}{x_2^{}},a\bigr) \) eine Quadrik beschrieben, die man die Schmiegquadrik an den Graph \( \) an der Stelle \(a\) (oder im Punkt \((a_1,a_2,f(a))\transp \) auf dem Graph von \(f\)) nennt.
Beispiele von Schmiegquadriken:

\(f\binom xy=x\,\sin x\,\cos y\),
Schmiegquadrik an der Stelle \(\binom00\): \(z=x^2\)
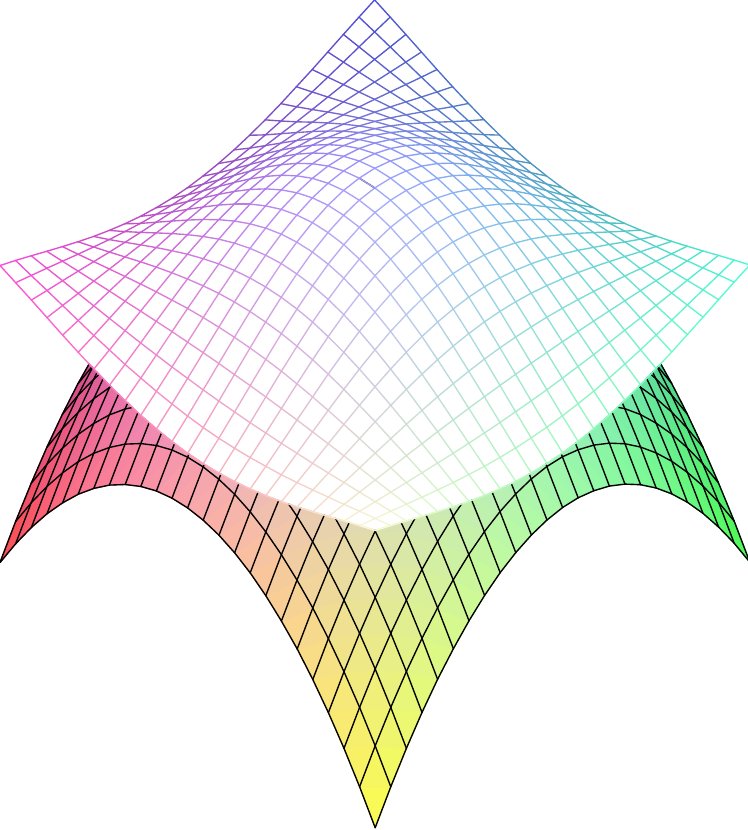
\(f\binom xy=\cos x\,\cos y\),
Schmiegquadrik an der Stelle \(\binom00\): \(z=1-\frac12\,(x^2+y^2)\)
von Schmiegquadriken finden Sie in der Online-Version des 3D-Modells zum Thema.
Dieses 3D-Modell gibt es auch real: Wenn Sie mich wieder in meinem Büro besuchen dürfen, verschaffe ich Ihnen Zugang.



Das 3D-Modell zeigt die Schmiegquadriken an drei verschiedenen Punkten auf dem Graphen von \( f\colon \mathbb{R}^2\rightarrow\mathbb{R}\colon \) \( \binom xy\mapsto\cos(x)\cos(y) \).
Die rote Quadrik ist ein elliptisches Paraboloid, die blaue und die grüne sind hyperbolische Paraboloide (also Sattelflächen).
Wir betrachten wieder \( f\in\Cf3D \) für eine Funktion \(f\) in zwei Variablen (also \( D\subseteq\RR^2 \)).
Man nennt den Punkt \( \bigl(a_1^{},a_2^{},f\binom{a_1^{}}{a_2^{}}\bigr)\transp \) auf dem Graphen \(\Gamma_f\)
Als einen Spezialfall des Satzes von Taylor 4.4.12 (nämlich für \(k = 0\)) erhalten wir ein wichtiges Ergebnis:
Es sei \( D\subseteq\RR^n \) konvex, \( a\in \inn{D} \) und \( f\in\Cf1D \).
Dann gibt es zu jedem \( x\in\inn{D} \) ein \( \vartheta\in(0,1)\) mit
\( f(x) \) \( {}= f(a)+\grad f(\tilde x)\skalp(x-a) \)
für \( \tilde x:= a + \vartheta\,(x-a) \).
Jede Approximation der Form
\( f(x) \) \( = c_0^{} + \sum\limits_{j=1}^n c_j^{}\,(x_j^{}-a_j^{}) \) \( + \sum\limits_{j,\ell=1}^n c_{j\,\ell}^{}\,(x_j^{}-a_j^{})\,(x_\ell^{}-a_\ell^{}) \) \( + \cdots \) \( + \) \( \sum\limits_{\! j_1^{},\ldots,j_k^{}=1}^n c_{j_1^{}\,\ldots\,j_k^{}}^{}\,(x_{j_1}^{}-a_{j_1}^{})\cdots(x_{j_k}^{}-a_{j_k}^{}) \) \( + o\left(\vert x-a\vert^k\right) \)
stimmt mit der Approximation durch das Taylorpolynom der Stufe \(k\) überein.
Insbesondere kann man Taylorpolynome aus Reihenentwicklungen ablesen:
Wir wollen die Funktion
\( f\colon \RR^2\to\RR\colon \) \( \binom xy \mapsto \E^{x+y} \)
an der Stelle \( a=\binom 00 \) quadratisch approximieren.
Mit \( \color{violet}{f\binom 00=1} \) und \( \color{blue}{\grad f\binom 00 = \binom 11} \) sowie \( \color{red}{\Hesso{f\binom 00} = \binom{1\,1}{1\,1} } \) erhalten wir:
\( f\binom xy \) \( = \color{violet}{1} \) \( {} + \color{blue}{(1,1)}\binom xy \) \( {} + \frac12\,(x,y)\bigl({\color{red}{\Hesso{f\binom00}}}\bigr)\binom xy \) \( {} + o\left(\vert(x,y)-(0,0)\vert^2\right) \)
\( {} = 1 + x+y \) \( {} + \frac12\,\bigl(x^2+2\,x\,y+y^2\bigr) \) \( {} + o\left(\vert(x,y)\vert^2\right) \).
Also ist das Taylorpolynom zweiter Stufe
\( T_2(f,\binom xy,\binom 00 \) \( {} =1 + x+y + \frac12\,\bigl(x^2+2\,x\,y+y^2\bigr) \).
Man erhält dies auch, indem man \(z = x + y\) in die Exponentialreihe \( \exp z = \sum\limits_{j=0}^\infty \frac{z^j}{j!} \) einsetzt, und die niedrigen Potenzen von \(z\) ausmultipliziert:
\( \exp(x+y) \) \( {} = \sum\limits_{j=0}^\infty \frac{(x+y)^j}{j!} \)
liefert die Partialsumme
\( \sum\limits_{j=0}^2 \frac{(x+y)^j}{j!} \) \( {} = (x+y)^0 + (x+y)^1 + \frac12(x+y)^2 \) \( {} = 1 + (x+y) + \frac12(x^2+xy+y^2) \).
| ↰ 4.1 | Material | 4.5 → |
| ← 4.3 | HM 2 | 5.1 ↳ |