\(
\def\pause{}
\def\,{\kern.2em}
\def\implies{\Longrightarrow}
\newcommand{\alert}[1]{{\color{red}{#1}}}
\newcommand{\blau}[1]{{\color{blue}{#1}}}
\newcommand{\orange}[1]{{\color{RebeccaPurple}{#1}}}
\def\ds{\displaystyle}
\let\epsilon\varepsilon
\let\subseteq\subseteqq
\let\supseteq\supseteqq
\let\setminus\smallsetminus
\let\le\leqq
\let\leq\leqq
\let\ge\geqq
\let\geq\geqq
\newcommand{\CC}{\mathbb C}
\newcommand{\NN}{\mathbb N}
\newcommand{\QQ}{\mathbb Q}
\newcommand{\RR}{\mathbb R}
\newcommand{\ZZ}{\mathbb Z}
\renewcommand{\Re}{\mathop{\mathrm{Re}}}
\renewcommand{\Im}{\mathop{\mathrm{Im}}}
\newcommand{\Bar}[1]{\overline{#1}}
\newcommand{\Pol}[2]{\mathop{\mathrm{Pol}}\nolimits_{#1}{#2}}
\renewcommand{\limsup}{\mathop{\overline{\mathrm{lim}}}}
\renewcommand{\liminf}{\mathop{\underline{\mathrm{lim}}}}
\newcommand{\redlimsup}{\mathop{\color{red}{\overline{\mathrm{lim}}}}}
\newcommand{\redliminf}{\mathop{\color{red}{\underline{\mathrm{lim}}}}}
\newcommand{\konv}[1][]{\mathbin{\mathop{\longrightarrow}\limits_{#1}}}
\newcommand{\bigset}[2]{\left\{{#1}\left|\strut
\vphantom{#1}\vphantom{#2}\right.\, {#2}\right\}}
\newcommand{\set}[2]{\left\{\smash{#1}\left|%
\vphantom{\smash{#1}}\vphantom{\smash{#2}}\right.\,\smash{#2}\right\}}
\newcommand{\E}{\mathrm{e}}
\newcommand{\I}{\mathrm{i}}
\newcommand{\diff}{\mathop{\mathrm{\kern0pt d}}}
\newcommand{\diffAt}[3]{\frac{\diff}{\diff{#2}}\,\left.{\vphantom{\frac00}#1}\,\right|_{#2=#3}}
\newcommand{\partAt}[3]{\frac{\partial}{\partial{#2}}\,\left.{\vphantom{\frac00}#1}\,\right|_{#2=#3}}
\newcommand{\diffgleich}{\mathbin{\,\mathop{=}\limits^{\,\prime}}\,}
\newcommand{\grad}{\mathop{\mathrm{grad}}}
\newcommand{\Jac}[2]{\mathrm{J}{#1}\left(#2\right)}
\newcommand{\Hesse}[2]{\mathrm{H}{#1}\left(#2\right)}
\newcommand{\Hesso}[1]{\mathrm{H}{#1}}
\newcommand{\transp}{^{^{\scriptstyle\intercal}}}
\newcommand{\inn}[1]{{#1}^\circ}
\newcommand{\Cf}[2]{\mathcal C^{#1}(#2)}
\newcommand{\skalp}{\mathbin{\scriptstyle\bullet}}
\newcommand{\IA}{{\sf\color{DarkGreen}{(IA)}}}
\newcommand{\IH}{{\sf\color{DarkGreen}{(IH)}}}
\newcommand{\IS}{{\sf\color{DarkGreen}{(IS)}}}
\)
Es sieht so aus, als hätten Sie Java-Script deaktiviert.
Ohne Java-Script kann diese Seite nicht lesbar dargestellt
werden
(die Seite
verwendet MathJax
und CindyJS ).
0.3 Der Körper \(\CC\) der komplexen Zahlen
Auch die reellen Zahlen reichen noch nicht aus.
Zum Beispiel hat zwar das Polynom \(X^2-2\) eine reelle Nullstelle
(sogar zwei: die — irrationalen — Zahlen \(\sqrt2\) und \(-\sqrt2\)) ,
aber das Polynom \(X^2+1\) hat noch keine Nullstellen.
Wir werden als Nächstes den Zahlenbereich so erweitern,
dass jedes nicht konstante Polynom eine Nullstelle hat.
0.3.1 Konstruktion
Auf der Menge aller geordneten Paare reeller Zahlen setzen wir die folgenden
Operationen fest:
\(
\begin{array}{rl}
(a,b)+(x,y) &:= (a+x,b+y) \\
(a,b)\cdot(x,y) &:= (ax-by,ay+bx) \,.
\end{array}
\)
Wir setzen außerdem \(\I:=(0,1)\) und identifizieren \(1\) mit \((1,0)\).
Dies führt zur Schreibweise \(a+b\I\) für \((a,b)=a\,(1,0)+b\,(0,1)\).
Den so gewonnenen Rechenbereich nennt man den
Körper \(\CC\) der komplexen Zahlen
Für \(w:=a+b\I\in\CC\) (mit \(a,b\in\RR\)) nennt man \(\Re w:=a\) den
Realteil
und \(\Im w:=b\) den Imaginärteil von \(w\).
0.3.2 Eigenschaften der komplexen Zahlen
Es seien \(a,b,x,y\in\RR\).
Man kann die Elemente von \(\RR\) mit denen der Form
\(a+0\I\) identifizieren (die Rechenregeln sind dieselben).
\((a+b\I)+(x+y\I)=(a+x)+(b+y)\I\)
\((a,b)+(x,y)=(a+x,b+y)\)
\((a+b\I)\cdot(x+y\I)=(ax-by)+(ay+bx)\I\)
\((a,b)\cdot(x,y)=(ax-by,ay+bx)\)
insbesondere: \(\I^2=-1\)
\((0,1)\cdot(0,1)=(-1,0)\)
\(a\cdot(x+y\I)=ax+ay\I\).
\((a+b\I)(a-b\I)=a^2+b^2 \blau{{}+0\I}\)
kann als reelle Zahl \(a^2+b^2\) interpretiert werden
(sogar als Element von \(\RR^+_0\) ).
Wir schreiben \(\Bar{a+b\I}:=a-b\I\) und nennen
\(\Bar z\)
die zu \(z\) komplex konjugierte Zahl .
0.3.3 Ring- und Körperaxiome
Eine Menge \(R\) mit zwei Operationen~\(+\) und~\(*\) heißt ein
Ring , wenn die folgenden Bedingungen erfüllt sind:
Assoziativität von \(+\) :
\(\forall\, a,b,c\in R\colon\, (a+b)+c=a+(b+c)\)
Kommutativität von \(+\) :
\(\forall\, a,b\in R\colon\, a+b=b+a\)
Neutralelement für \(+\) :
\(\exists\, \orange{0}\in R\,
\forall\, a\in R\colon\, a+\orange{0}=a=\orange{0}+a\)
Inverse für \(+\) :
\(\forall\, a\in R\,\exists\, b\in R\colon\,
a+b=\orange{0}\)
Assoziativität von \(*\) :
\(\forall\, a,b,c\in R\colon\, (a*b)*c=a*(b*c)\)
Neutralelement für \(*\) :
\(\exists\, \orange{e}\in R\,
\forall\, a\in R\colon\, a*\orange{e}=a=\orange{1}*a\)
Distributivität:
\(
\forall\, a,b,c\in R\colon\,
\begin{array}[t]{ccc}
a*(b+c) &=& (a*b)+(a*c) \\
(b+c)*a &=& (b*a)+(c*a)
\end{array}
\)
Ein Ring \((R,+,*)\) heißt Körper , wenn außerdem gilt:
Kommutativität von \(*\) :
\(\forall\, a,b\in R\colon\, a*b=b*a\)
Inverse für \(*\) :
\(\forall\, a\in R\setminus\{0\}\,
\exists\, c\in R\colon\,
a*c=\orange{e}=c*a\)
Meistens schreibt man \(0\) statt \(\orange{n}\) und \(1\) statt \(\orange{e}\).
Diese Axiome beschreiben die Grundregeln, nach denen wir algebraische Terme
umformen können. Jede kompliziertere Umformung muss sich auf diese Axiome
zurückführen lassen.
Diese Grundregeln gelten auch in vielen anderen
Bereichen (in denen man also wie mit Zahlen rechnen kann). Wir geben
einige Beispiele, weitere (etwa gewisse Mengen von Matrizen) lernt man in
der linearen Algebra kennen:
0.3.4 Beipiele
\((\ZZ,+,\cdot)\) ist ein Ring.
\((\QQ,+,\cdot)\) ist ein Körper.
\((\RR,+,\cdot)\) ist ein Körper.
\((\CC,+,\cdot)\) ist ein Körper.
Die Menge \(\Pol{}\RR\) aller Polynome mit Koeffizienten aus
\(\RR\) ist ein Ring.
Die Menge \(\Pol{}\CC\) (Polynome mit Koeffizienten aus \(\CC\)) ist
ein Ring.
Die Menge \(\Pol{}\ZZ\) (Polynome mit Koeffizienten aus \(\ZZ\)) ist
ein Ring.
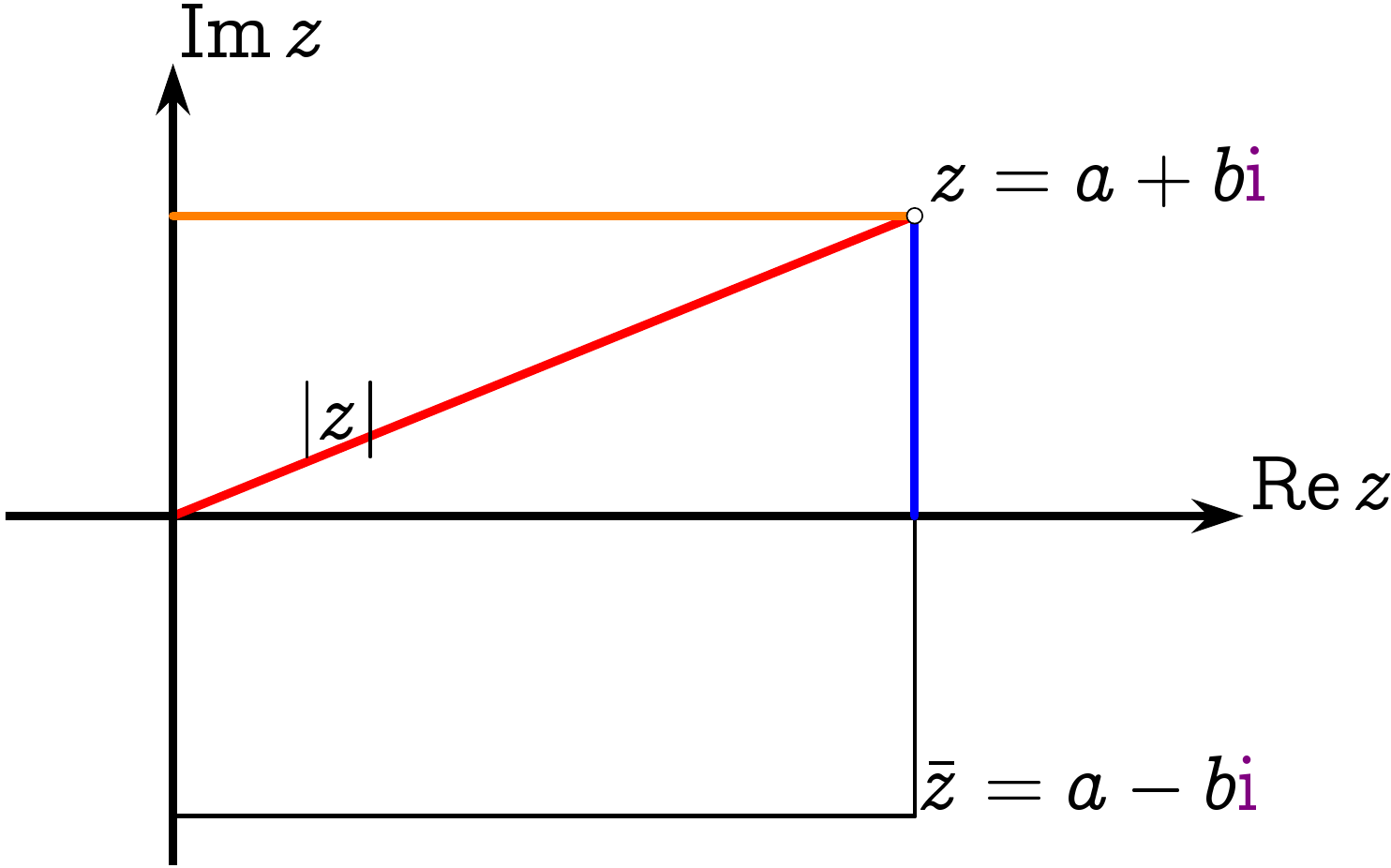
0.3.5 Komplexe Konjugation, Betrag
Für \(z=a+b\I\in\CC\) mit \(a,b\in\RR\) setzen wir
\(\alert{\Bar z}:=\Bar{(a+b\I)} :=a\alert{-}b\I\)
\(\alert{|z|}:=\sqrt{z\,\Bar z}
=\sqrt{a^2+b^2}\)
0.3.6 Mehr Eigenschaften der komplexen Zahlen
Seien \(z,w\in\CC\).
\(z\in\RR\iff \Bar z=z\)
\(\Bar{z+w}=\Bar z+\Bar w\),
\(|\Bar z|=|z|\), \(z\cdot\Bar z=|z|^2\)
\(\Bar{\biggl(\frac1z\biggr)}=\frac1{\Bar z} =\frac z{\,|z|^2}\)
(falls \(z\ne0\))
\(|z\cdot w|=|z|\cdot|w|\),
\(\left|\frac zw\right|=\frac{|z|}{|w|}\) (falls \(w\ne0\))
\(|z+w|\le|z|+|w|\)
(Dreiecksungleichung)
0.3.7 Konsequenz aus der Dreiecksungleichung
Es seien \(z_1,z_2\in\CC\).
Aus \(|z_1|=|z_1+\blau{z_2-z_2}| \le|z_1+z_2|+|-z_2| \)
ergibt sich:
\(
\left|\strut|z_1|-|z_2|\right|\le|z_1+z_2|
\).