| ↰ 0.1 | Material | 0.5 → |
| ← 0.3 | HM 2 | 1.1 ↳ |
Für jede komplexe Zahl \(z\ne0\) gibt es ein \(\phi\in\RR\) so, dass gilt:
\(\begin{array}[t]{ccl} \alert{z} &\alert=& \alert{|z|\,(\cos\phi+\I\sin\phi)}\\ &= &|z|\,\cos\phi+\I\,|z|\,\sin\phi \,. \end{array}\)
Wegen der Periodizität der Winkelfunktionen ist \(\phi\) nur bis auf Addition eines ganzzahligen Vielfachen von \(2\,\pi\) festgelegt.
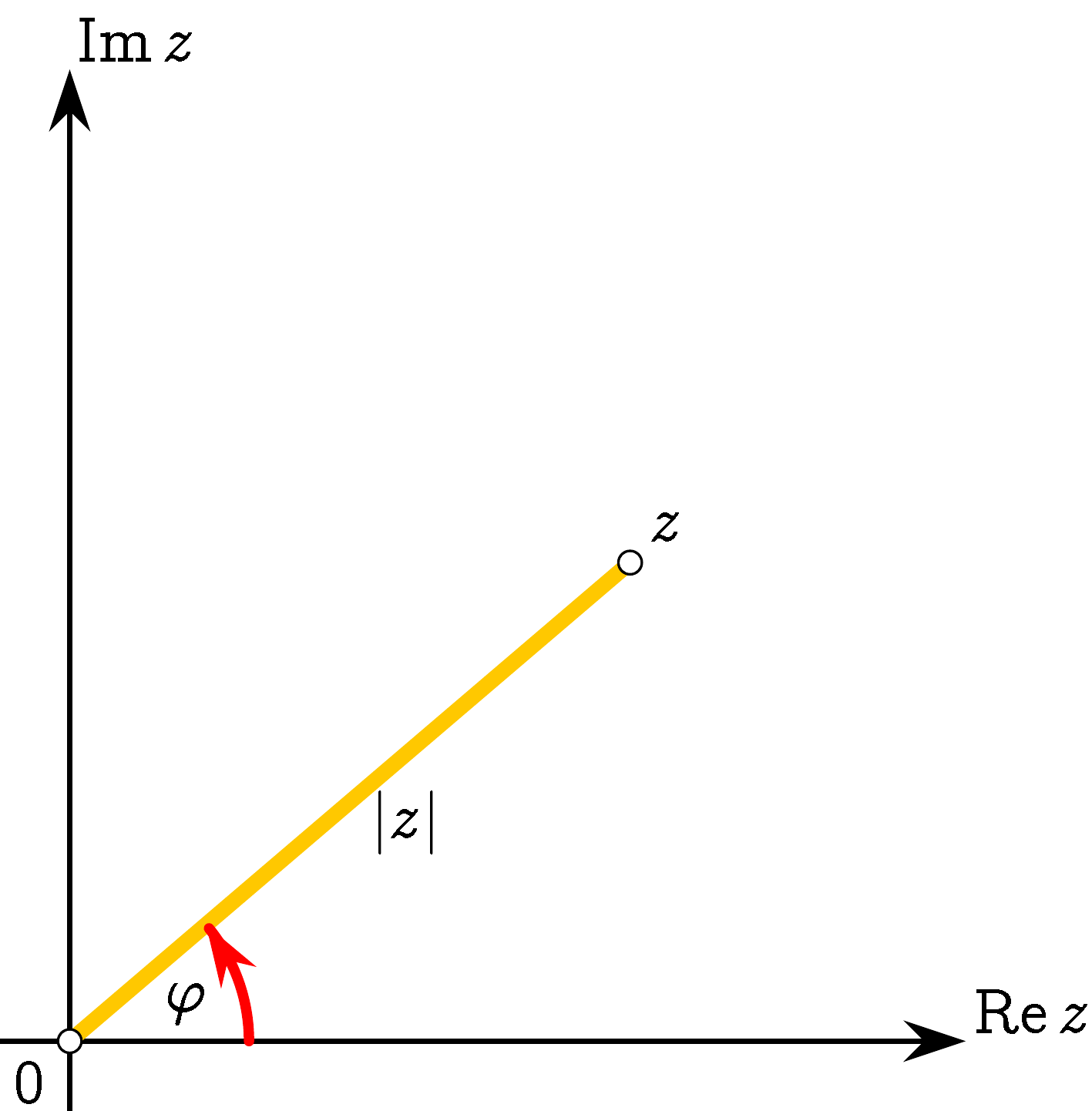
(Wir verwenden das Bogenmaß zur Angabe des Winkels).
Um Eindeutigkeit zu erreichen, verlangt man \(\alert{0\leqq\phi \lt 2\,\pi}\).
Ist dies erfüllt, nennt man \(\alert\arg z:=\phi\) das Argument von \(z\).
Es seien \(z=|z|\,(\cos\phi+\I\sin\phi)\) und \(z'=|z'|\,(\cos\psi+\I\sin\psi)\).
Dann gilt:
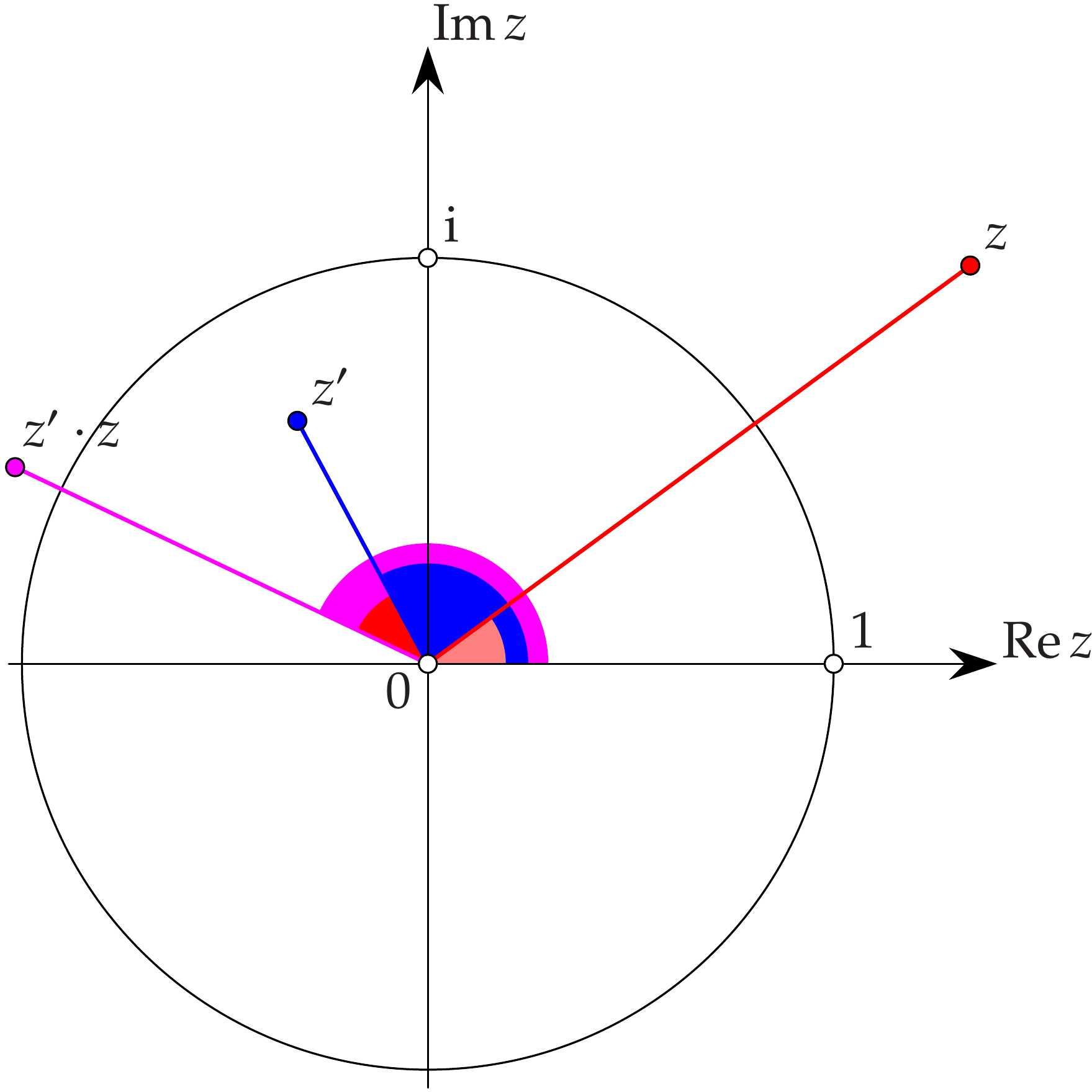
Man multipliziert also komplexe Zahlen, indem man ihre Beträge multipliziert und ihre Argumente addiert.
Eine interaktive Version dieses Bildes findet man unter https://info.mathematik.uni-stuttgart.de/HM-Stroppel-Material/Polarkoordinaten/
Zum Nachweis der Regel für die Multiplikation benutzt man das Additionstheorem (das sich ergibt aus der Formel von Euler und de Moivre, siehe 1.14.18):
Für \(s,t\in\RR\) gilt
Es sei \(n\in\NN\) und \(z=r\,(\cos\beta+\I\sin\beta)\in\CC{} \setminus\{0\}\).
Gesucht ist eine \(n\)-te Wurzel aus \(z\), also \(w=s\,(\cos\phi+\I\sin\phi)\in\CC\) mit \(w^n=z\).
Ansatz:
\( w^n=z \iff{} s^n\,\left(\strut\cos(n\phi)+\I\sin(n\phi)\right) = r\,(\cos\beta+\I\sin\beta) \,. \)
Durch Vergleich von Real- und Imaginärteilen ergibt sich \(s=\sqrt[n]{r}\) und \(n\phi=\beta\alert{+2\,\pi\ell}\) mit \(\ell\in\ZZ\) [wg. der Periodizität von \(\cos\) und \(\sin\)], also \( \phi\in\set{\frac\beta n+\ell\,\frac{2\,\pi}n}{\ell\in\ZZ} \).
Wegen der Periodizität der Winkelfunktionen kann man sich auf Werte von \(\ell\) im Intervall \([0,n-1]\) beschränken.
Man erhält also \(\alert{n}\) verschiedene \(n\)-te Wurzeln.
In 0.4.4 haben wir gesehen, dass Polynome der Form \(X^n-z\) mit \(z\in\CC\setminus\{0\}\) stets \(n\) verschiedene Nullstellen in \(\CC\) haben.
Der folgende Satz ist viel allgemeiner, sein Beweis liegt aber tief und würde uns hier zu weit führen:
Jedes Polynom \(p(X)=X^n+a_{n-1}X^{n-1}+\cdots+a_1X^{\blau1}+a_0\blau{X^0}\) mit \(a_0,\ldots,a_{n-1}\in\CC\) und \(n\ge1\) besitzt mindestens eine Nullstelle in \(\CC\).
Der Fundamentalsatz besagt, dass jedes Polynom mit komplexen Koeffizienten wenigstens eine Nullstelle hat — außer den Konstanten:
Man kann durch Division durch den Leitkoeffizienten stets die in 0.4.5 verlangte Form erreichen.
Die üblichen Formeln
(Mitternachtsformel
, \(p-q\)-Formel
, …) zur
Lösung quadratischer Gleichungen in den reellen Zahlen
lassen sich allgemeiner auch zur Nullstellenbestimmung bei
quadratischen Polynomen mit komplexen Koeffizienten verwenden
— wenn man die Schreibweise \(\pm\sqrt z\) geeignet
interpretiert.
Wer das detaillierter erklärt haben möchte, wird vielleicht von unserer Abhandlung profitieren: Praktische Bestimmung der Lösungen einer quadratischen Gleichung in komplexen Zahlen (mit vertieftem Hintergrundwissen).
Ist \(x_0\) eine Nullstelle von \(p(X)=X^n+a_{n-1}X^{n-1}+\cdots+a_1X+a_0\), so gibt es ein Polynom \(q(X)\) mit \(p(X)=q(X)(X-x_0)\).
Aus dem Fundamentalsatz 0.4.5 folgt, dass sich jedes Polynom \(p(X)=X^n+a_{n-1}X^{n-1}+\cdots+a_1X+a_0\) darstellen lässt als
\( p(X)=(X-z_1)\cdot(X-z_2)\cdots(X-z_n) \,. \)
Dabei können manche der \(z_j\) gleich sein: die Anzahl der Faktoren \((X-z_j)\) nennt man die Vielfachheit der Nullstelle \(z_j\) in \(p(X)\). Die Faktoren \((X-z_j)\) heißen Linearfaktoren.
Ist \(p(X)=a_{n}X^n+a_{n-1}X^{n-1}+\cdots+a_1X+a_0 \in\Pol{}\ZZ\) ein Polynom mit ganzzahligen Koeffizienten (also \(a_{n},\ldots,a_0\in\ZZ\)), so ist jede ganzzahlige Nullstelle ein Teiler von \(a_0\).
Im Fall \(a_0\ne0\) besitzt \(a_0\) nur endlich viele Teiler, man kann also algorithmisch alle ganzzahligen Nullstellen von \(p(X)\) bestimmen.
| ↰ 0.1 | Material | 0.5 → |
| ← 0.3 | HM 2 | 1.1 ↳ |