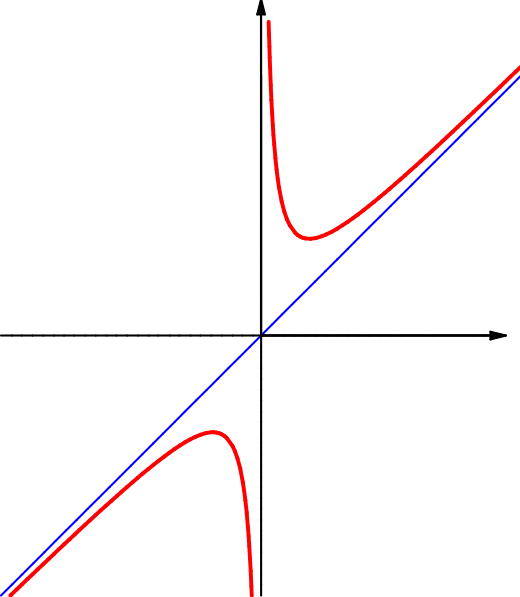
(Zur besseren Veranschaulichung ist die Winkelhalbierende \(y = x\) mit eingezeichnet.)
| ↰ 1.1 | Material | 1.12 → |
| ← 1.10 | HM 2 | 2.1 ↳ |
Wir wollen eine Funktion an Löchern im Definitionsbereich oder am Rand stetig ergänzen - so weit das möglich ist.
Wir betrachten dazu Punkte im Abschluss des Definitionsbereichs
(d. h.: Punkte \(x_0\), für die jede Umgebung von \(x_0\) wenigstens einen
Punkt des Definitionsbereichs enthält)
- bei Punkten, die vom Definitionsbereich isoliert liegen, können wir
nicht erwarten, dass die Funktion sich eindeutig (stetig) fortsetzen
lässt!
Wir führen die folgenden Begriffe ein:
Gegeben seien eine Funktion \(f \colon M \to \RR\) mit Definitionsbereich \(M\subseteq\RR\) und \(x_0\) im Abschluss von \(M\).
Manchmal werden auch die Kurzschreibweisen \( f(x_0 {\color{red}{{}+0}}) := \lim\limits_{x\to x_0{\color{red}{{}+0}}}f(x)=g \) bzw. \( f(x_0\ {\color{red}{{}-0}}) := \lim\limits_{x\to x_0{\color{red}{{}-0}}}f(x)=g \) benutzt.
Anschaulich ausgedrückt: Beim rechtsseitigen Grenzwert suchen wir die Grenzlage von \(f (x )\), wenn \(x\) von rechts gegen \(x_0\) strebt.
Selbst wenn sowohl ein rechts- als auch ein linksseitiger Grenzwert existiert, braucht es keinen beidseitigen Grenzwert zu geben:
Die Funktion
\( f \colon \RR \setminus\{0\} \to \RR \colon x \mapsto \dfrac{|x |}{x} \) \( {} = \begin{cases} -1 & \text{ falls $x \lt 0$,}\\ \phantom-1 & \text{ falls $x \gt 0$} \end{cases} \)
hat in \(x_0 =0\) die einseitigen Grenzwerte
\( \lim\limits_{x\to 0-0}f(x) \) \( {} = \lim\limits_{x\to 0-0}-1 \) \( {} = -1 \)
und\( \lim\limits_{x\to 0+0}f(x) \) \( {} = \lim\limits_{x\to 0+0}1 \) \( {} = 1 \).
Analog zur bestimmten Divergenz von Folgen 1.4.10 betrachtet man auch bestimmte Divergenz von Funktionen gegen \(+\infty\) oder gegen \(-\infty\).
Wir erweitern die Begriffsbildung, um das Verhalten einer Funktion an den Rändern „im Unendlichen“ zu beschreiben. Wir müssen dabei sicherstellen, dass „\(+\infty\) im Abschluss von \(M\) liegt“.
Es sei \(f \colon M \to \RR\) eine Funktion.
Die Funktion \(f \colon \RR \setminus\{0\} \to \RR \colon x \mapsto \frac1x \) hat in \(+\infty\) und \(-\infty\) jeweils den Grenzwert \( \lim\limits_{x\to+\infty}f(x)=0 \) und \( \lim\limits_{x\to-\infty}f(x)=0 \).
Das Verhalten bei \(x_0\) = 0 wird beschrieben durch \( \lim\limits_{x\to0-0}f(x)=-\infty \) und \( \lim\limits_{x\to0+0}f(x)=+\infty \).
Die Funktion \( f\colon\RR\setminus\{0\}\to\RR\colon{}\pause x\mapsto x+\frac1x \) ist in \(+\infty\) und \(-\infty\) jeweils bestimmt divergent:
\( \lim\limits_{x\to+\infty}f(x)=+\infty \)
Das Verhalten bei \(x_0\) = 0 wird beschrieben durch \( \lim\limits_{x\to-\infty}f(x)=-\infty \).

(Zur besseren Veranschaulichung ist die Winkelhalbierende \(y = x\) mit eingezeichnet.)
Wir betrachten die Funktion \( f \colon M \to \RR \colon x \mapsto x\mapsto \dfrac{x^3+2\,x+1}{3\,x^3+5} \).
Dabei ist \( M:=\RR\setminus\set{x\in\RR}{3\,x^3=-5} \).
Explizit müssen wir den Punkt \( x_0 := -\sqrt[3]{\frac53} \) ausnehmen.
Eine erste Skizze des Graphen sieht so aus:
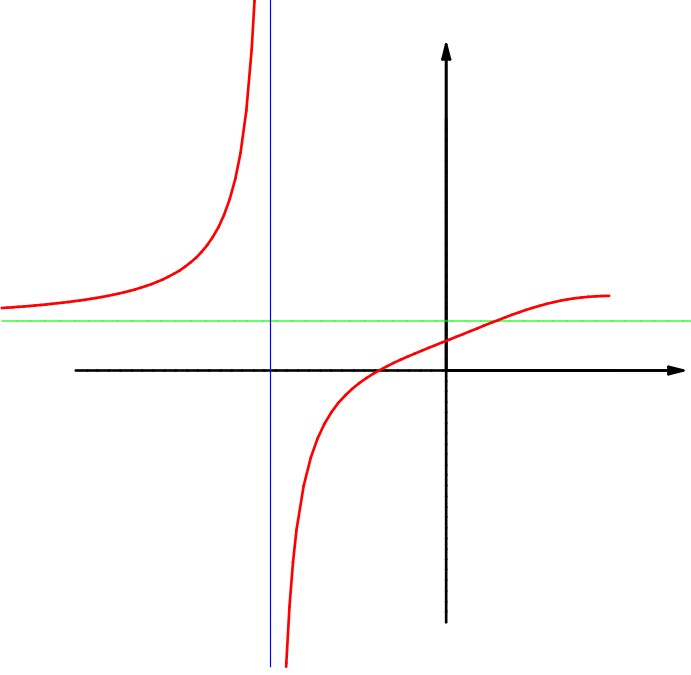
Offenbar gilt \( \lim\limits_{x\to x_0-0}f(x)=+\infty \) und \( \lim\limits_{x\to x_0+0}f(x)=-\infty \).
Was kann man über \( \lim\limits_{x\to+\infty}f(x) \) oder \( \lim\limits_{x\to-\infty}f(x) \) sagen?
Eine etwas bessere Skizze des Graphen (hier können Sie die (hell bzw. dunkel) roten und blauen Punkte auf der \(x\)-Achse interaktiv bewegen, um das Grenzverhalten zu erahnen) führt auf die Vermutung \( \lim\limits_{x\to-\infty}f(x) =\dfrac13 = \lim\limits_{x\to+\infty}f(x) \).
Diese Vermutung ist korrekt, dies ergibt sich aus einem allgemeinen Ergebnis:
Es sei \(f \colon M \to \RR\) eine gebrochen rationale Funktion, also \( f(x)=\frac{a(x)}{b(x)} \,, \) mit Polynomen \( a(x)=a_n\,x^n+\cdots+a_0 \) und \( b(x)=b_k\,x^k+\cdots+b_0 \), und \( M=\RR\setminus\set{x\in\RR}{b(x)=0} \).
Sind \(n\) und \(k\) minimal gewählt (also \( a_n\ne0\pause\ne b_k \) ), so gilt:
Für \( \lim\limits_{x\to-\infty} f(x) \) gelten analoge Regeln, man muss aber noch berücksichtigen, ob \(n\) bzw. \(k\) gerade oder ungerade ist.
Eine Funktion \(f \colon M \to \RR\) heißt linksseitig (bzw. rechtsseitig) stetig in \(x_0\) , wenn gilt: \(x_0\in M\) und \( \lim\limits_{x\to x_0+0}f(x)=f(x_0) \) bzw. \( \lim\limits_{x\to x_0-0}f(x)=f(x_0) \,. \)
Eine Funktion \(f \colon M \to \RR\) ist genau dann stetig in \(x_0\), wenn sie links- und rechtsseitig stetig in \(x_0\) ist.
In diesem Fall gilt \( \lim\limits_{x\to x_0-0}f(x)=\lim\limits_{x\to x_0+0}f(x)\pause \quad\bigl[{}=f(x_0)\bigr] \).
(Diese Definition hat natürlich nur für solche Stellen \(x_0\) einen Sinn, für die \(x_0\in M\) gilt.)
| ↰ 1.1 | Material | 1.12 → |
| ← 1.10 | HM 2 | 2.1 ↳ |