| ↰ 1.1 | Material | 1.11 → |
| ← 1.9 | HM 2 | 2.1 ↳ |
Wir betrachten im Folgenden Funktionen, die reellen Zahlen wieder
reelle Zahlen zuordnen:
Also Abbildungen \(f \colon M \to \RR\) mit \(M \subseteq \RR\).
Jede solche Funktion kann man durch ihren Graph veranschaulichen: Man trägt \(y = f (x )\) über \(x\) auf, markiert also die Punkte mit Koordinaten \((x,f(x))\) für \(x\in M\).
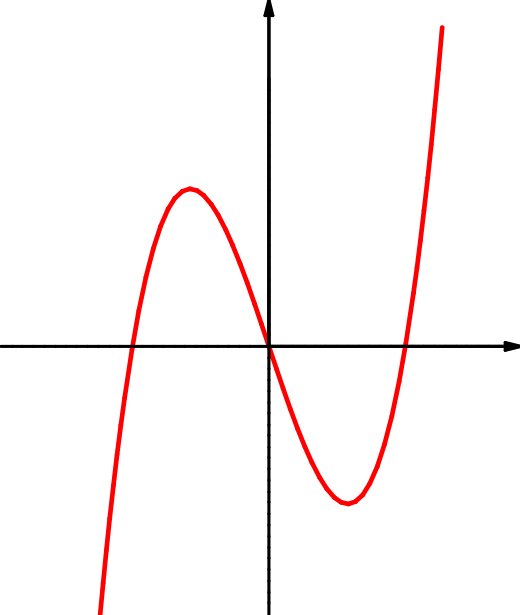
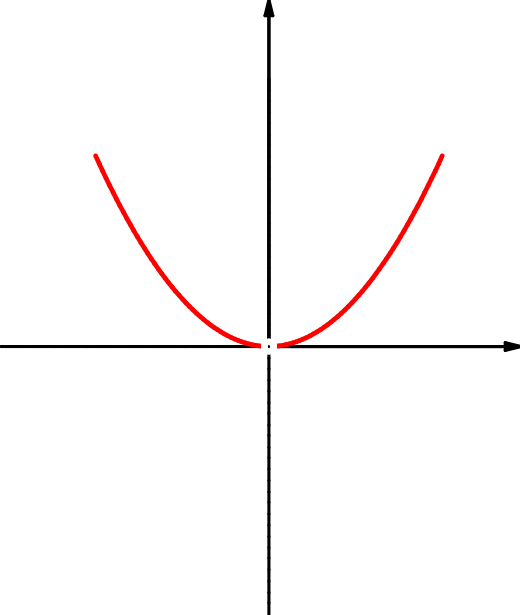
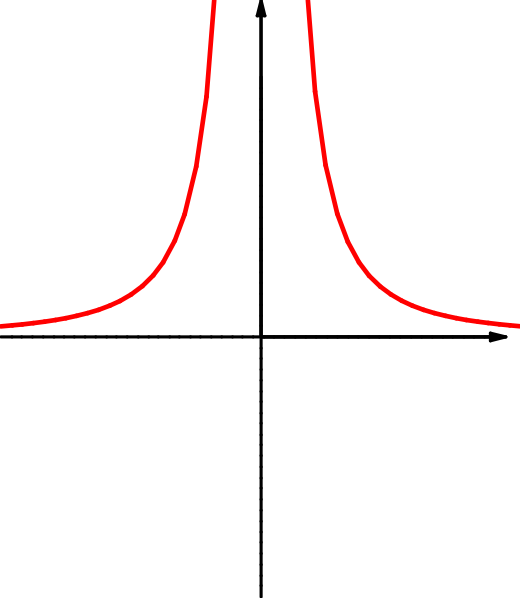
| \(f(x)=4\,x^3-3\,x\) | \(f(x)=\dfrac{x^3}x\) | \(f(x)=\dfrac1{x^2}\) |

|

|

|
| \(M=\RR\) | \(M=\RR\setminus\{0\}\) | \(M=\RR\setminus\{0\}\) |
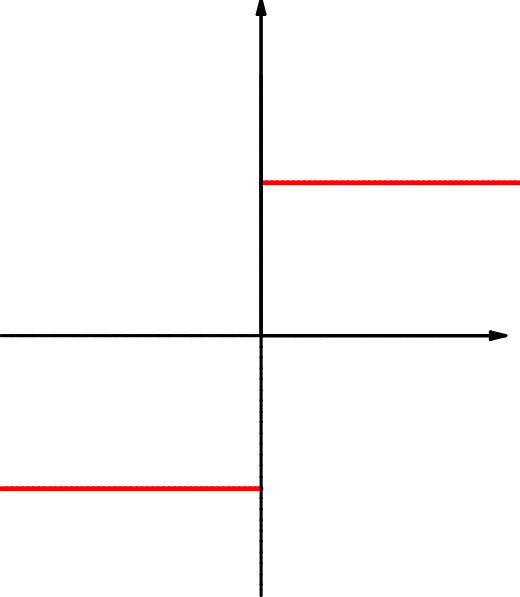
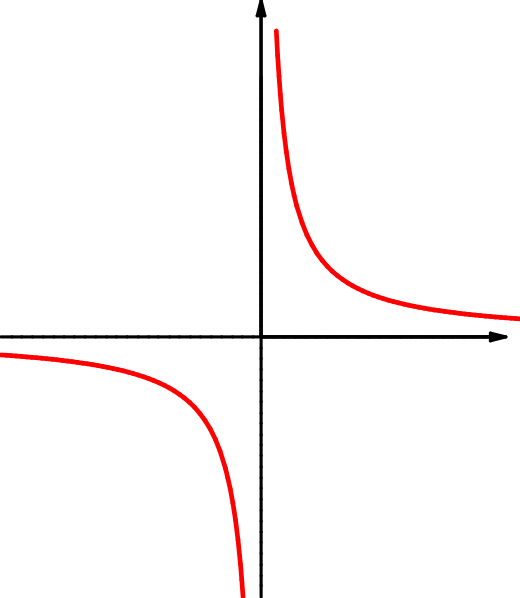
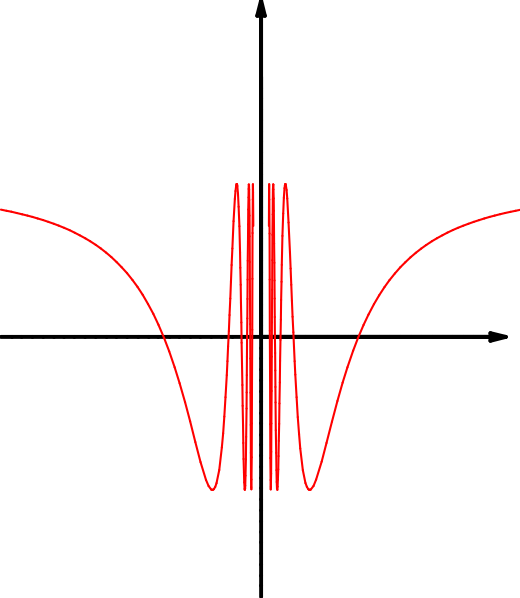
| \(f(x)=\dfrac{|x|}x\) | \(g(x)=\dfrac1x\) | \(h(x)=\cos(\dfrac1{x})\) |
|
|
|
| \(M=\RR\setminus\{0\}\) | \(M=\RR\setminus\{0\}\) | \(M=\RR\setminus\{0\}\) |
Bei manchen dieser Beispiele weisen die Graphen „Lücken“ oder „Sprünge“ auf. Manche dieser Lücken kann man „sinnvoll“ durch Ergänzung schließen. Bei den Beispielen in 1.10.2 ist das aber nicht möglich. Wir wollen unser Gefühl präzisieren, das uns sagt, welche Ergänzung des Graphen „sinnvoll“ ist.
Das Verhalten der Funktionen in den Beispielen aus 1.10.2 können Sie
sich hier interaktiv veranschaulichen:
Sie sehen die drei Graphen übereinander gezeichnet.
Bewegen Sie jeweils den mit "\(x\)" markierten Punkt auf der
horizontalen Achse - der Punkt \((x,f(x))\) bzw. \((x,g(x))\) oder
\((x,h(x))\) wird sich auf dem Funktionsgraphen entsprechend mit
bewegen.
Es sei \(M \subseteqq \RR\), und es sei \(x_0 \in M\). Eine Funktion \(f \colon M \to \RR\) heißt stetig in \(x_0\), wenn gilt: Für jede Folge \( (x_j)_{j\in\NN}\) mit \( x_j\in M\) und \( \lim\limits_{j\in\NN}x_j=x_0 \) konvergiert die Folge \( \bigl(f(x_j)\bigr)_{j\in\NN} \) gegen \(f (x_0 )\).
Wir schreiben abkürzend \( x_j\konv[{j}]x_0 \) oder \( x_j\konv x_0 \), um \( \lim\limits_{j\in\NN}x_j=x_0 \) auszudrücken.
Die Funktion \(f\) heißt stetig auf \(M\), wenn sie in jedem Punkt von \(M\) stetig ist.
Wichtig ist, dass man wirklich jede Folge \( x_j\konv x_0 \) in \(M\) betrachtet!
Die Funktion \( f\colon \RR\to\RR \) sei definiert durch
Diese Funktion ist nicht stetig in \(x_0 = 0\), denn für die durch \( x_j:= \frac1j \) definierte Folge gilt \( x_j\konv 0 \) und \( f(x_j)\konv 0 \), aber \( 0\ne 1=f(0) \). Es gibt aber viele andere gegen \(0\) konvergente Folgen (z. B. \( \left(\frac\pi j\right)_{j\in\NN} \) für die die Folge der Funktionswerte gegen \(f (0)\) konvergiert!
Es ist sehr schwer, alle Folgen in den Griff
bekommen, die gegen eine Stelle \(x_0\) konvergieren.
Die folgende Beschreibung wirkt erst einmal abschreckend, wird aber
genau mit diesem fundamentalen Problem fertig:
Die Funktion \(f \colon M \to \RR\) ist genau dann stetig im Punkt \(x_0\) wenn gilt:
Dabei wird zuerst die Fehlertoleranz \(\epsilon\) vorgegeben: Die Schranke \(\delta = \delta_\epsilon\) hängt von der Wahl von \(\epsilon\) ab.
Man kann das auch so ausdrücken:
Die Funktion \(f \colon M \to \RR\) ist genau dann stetig im Punkt \(x_0 \in M\), wenn es zu jeder Umgebung \(U = U_\epsilon (f (x_0 ))\) eine Umgebung \(V = U_\delta(x_0)\) derart gibt, dass \(f (V\cap M) \subseteqq U\).
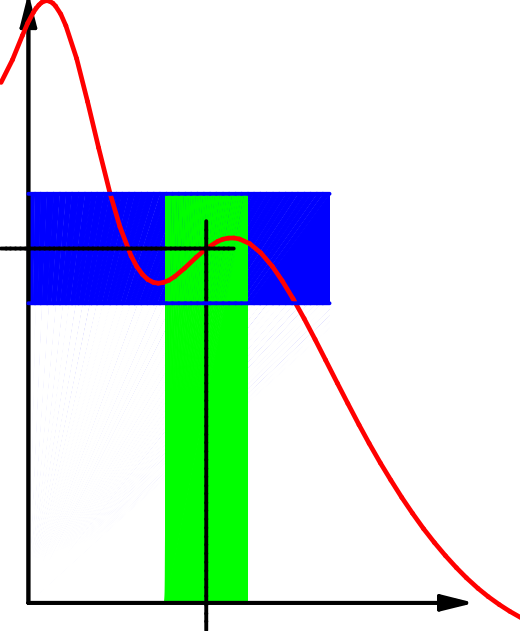
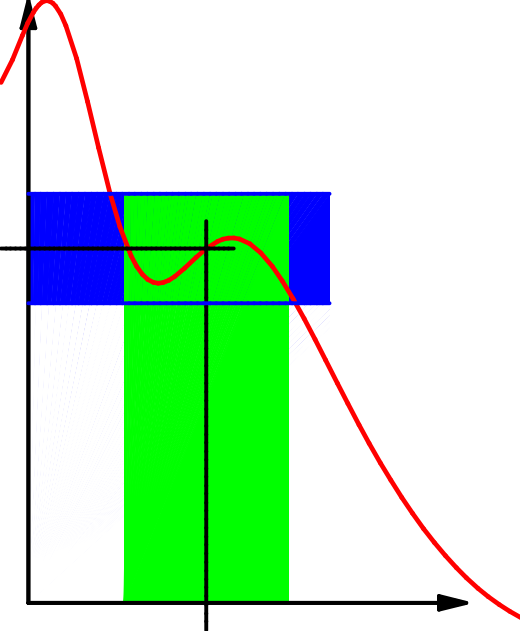
Die Beschreibung durch Umgebungen ist recht anschaulich:
|
|
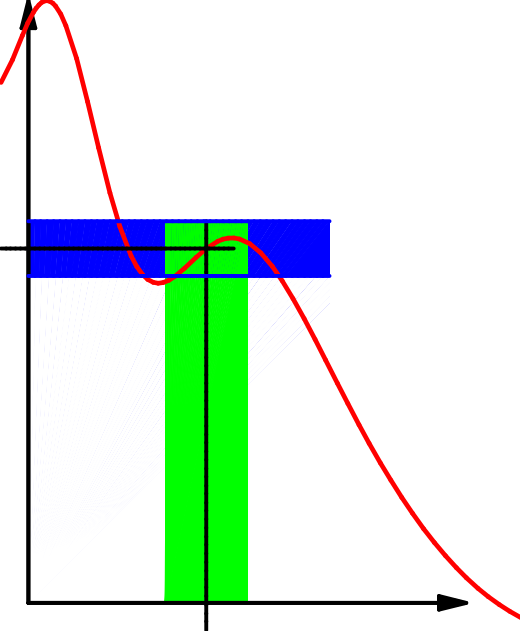
|
| \(x_0\qquad\) | \(x_0\qquad\) | \(x_0\qquad\) |
| Es gilt hier | aber | |
| \(f\bigl(U_\delta(x_0)\bigr)\subseteq U_\epsilon(f(x_0))\); | \(f\bigl(U_{2\,\delta}(x_0)\bigr)\subseteq U_\epsilon(f(x_0))\); | \(f\bigl(U_\delta(x_0)\bigr) \nsubseteq U_{\frac12\epsilon}(f(x_0))\). |
Ihnen ist das nicht anschaulich genug?
(verständlich...)
Ein interaktives Spielzeug dazu finden Sie hier.
| ↰ 1.1 | Material | 1.11 → |
| ← 1.9 | HM 2 | 2.1 ↳ |