1.12. Rechenregeln für Funktionsgrenzwerte

Wie bei Folgen und Reihen (vgl. 1.5.3 und 1.9.3) wollen wir auch das Verhalten von Funktionsgrenzwerten verstehen, wenn wir Funktionen addieren, multiplizieren, dividieren oder gegeneinander abschätzen.

1.12.1. Grenzwertsätze für Funktionen (von rechts).

Existieren \( \lim\limits_{x\to x_0+0} f(x) \) und \( \lim\limits_{x\to x_0+0} g(x) \) (als reelle Zahlen!), so gilt:

1. \( \lim\limits_{x\to x_0+0} \bigl(f(x)+g(x)\bigr) \pause =\lim\limits_{x\to x_0+0} f(x) + \lim\limits_{x\to x_0+0} g(x) \).
2. \( \lim\limits_{x\to x_0+0} \bigl(c\cdot f(x)\bigr) \pause =c\cdot\lim\limits_{x\to x_0+0} f(x) \) für jede reelle Zahl \(c\).
3. \( \lim\limits_{x\to x_0+0} \bigl(f(x)\cdot g(x)\bigr) \pause =\lim\limits_{x\to x_0+0} f(x) \cdot \lim\limits_{x\to x_0+0} g(x) \).
4. \( \lim\limits_{x\to x_0+0} \dfrac{f(x)}{g(x)} \pause =\dfrac{\lim\limits_{x\to x_0+0} f(x)}{\lim\limits_{x\to x_0+0} g(x)} \), falls \( \lim\limits_{x\to x_0+0} g(x)\ne0 \).
5. \( \lim\limits_{x\to x_0+0} f(x) \le \lim\limits_{x\to x_0+0} g(x) \) falls \( \forall\,x\in M\colon f(x)\le g(x) \).
6. \( \lim\limits_{x\to x_0+0} \bigl|f(x)\bigr| \pause =\bigl|\lim\limits_{x\to x_0+0} f(x) \bigr| \)
7. Existiert außer \( a:= \lim\limits_{x\to x_0+0} f(x) \) auch der Grenzwert \( \lim\limits_{x\to a} g(x) \), so gilt auch \( \lim\limits_{x\to x_0+0} g\bigl(f(x)\bigr) \pause =\lim\limits_{t\to a} g(t) \).

1.12.2. Grenzwertsätze für Funktionen (allgemein).

Es gilt

1. \( \lim\limits_{x\to x_0^{}-0}f(x) \pause = \lim\limits_{t\to x_0^{}+0}f(2\,x_0^{}-t) \),
2. \( \lim\limits_{x\to+\infty}f(x) \pause = \lim\limits_{t\to0+0}f\left(\frac1t\right) \),
3. \( \lim\limits_{x\to-\infty}f(x) \pause = \lim\limits_{t\to0-0}f\left(\frac1t\right) \).

Damit lassen sich die Aussagen von 1.12.1 übertragen auf Grenzwerte von links, beidseitige Grenzwerte, und Grenzwerte im Unendlichen.

1.12.3. Stetigkeit von Polynomfunktionen.

Es sei \( f(x)=\sum_{j=0}^n a_j\,x^j \pause =a_0+a_1\,x+\cdots+a_n\,x^n \). Dann gilt \( \lim\limits_{x\to x_0^{}}f(x) \) \({} = \lim\limits_{x\to x_0^{}} \sum_{j=0}^n a_j\,x^j \) \({} = \sum_\limits{j=0}^n\lim\limits_{x\to x_0^{}} a_j\,x^j \) \({} = \sum\limits_{j=0}^n a_j\,\lim\limits_{x\to x_0^{}} x^j \) \({} = \sum\limits_{j=0}^n a_j\,\bigl(\lim\limits_{x\to x_0^{}} x\bigr)^j \) \({} = \sum\limits_{j=0}^n a_j^{}\,x_0^j \) \({} = f(x_0^{}) \,. \)

Daraus folgt, dass jedes Polynom an jeder Stelle stetig ist.

Man kann aus bereits als stetig bekannten Funktionen neue stetige Funktionen gewinnen:

1.12.4. Satz.

Es seien \(f\) und \(g\) reellwertige Funktionen, die auf dem gemeinsamen Definitionsbereich \(M\) stetig sind.

Dann sind die folgenden Funktionen stetig auf \(M\):

1. \( f+g\colon M\to\RR\colon{}\pause x\mapsto f(x)+g(x) \)
2. \( f\cdot g\colon M\to\RR\colon{}\pause x\mapsto f(x)\cdot g(x) \)
3. Gilt \( g(x)\ne0 \) für alle \( x\in M \), so ist auch \( \frac fg\colon M\to\RR\colon{}\pause x\mapsto \frac{f(x)}{g(x)} \) stetig.
4. Ist \( h\colon L\to\RR \) stetig und gilt \( f(M)\subseteq L \), so ist auch die durch Hintereinanderausführung entstehende Funktion \( h\circ f\colon{}\pause M\to\RR\colon{}\pause x\mapsto h\bigl(f(x)\bigr) \) stetig.

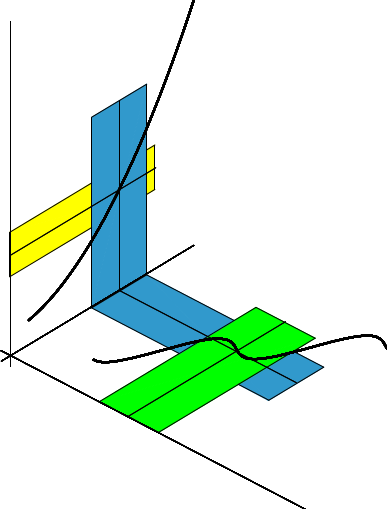
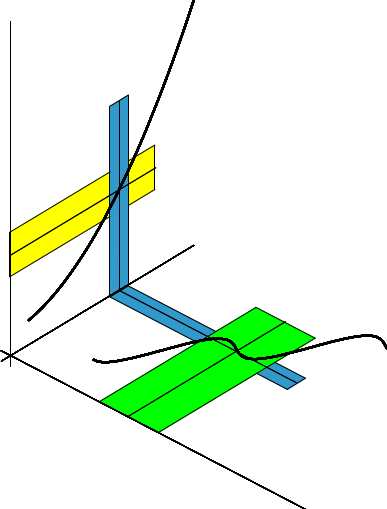
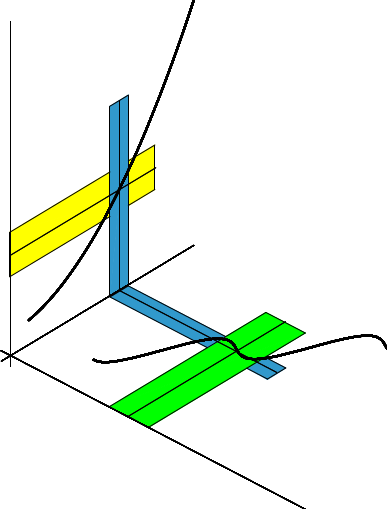
Die folgende Skizze veranschaulicht den Beweis der Stetigkeit der Verkettung \( h\circ f \):

Im \(x\)-\(y\)-Koordinatensystem sieht man den Graph von \(f\) und die Umgebungen \( U_\delta(x_0^{}) \) (in grün) sowie \( U_\gamma\bigl(f(x_0^{})\bigr) \) (in blau).

im \(y\)-\(z\)-System den Graph von \(h\) und die Umgebungen \( U_\gamma\bigl(f(x_0^{})\bigr) \) (immer noch blau) sowie \( U_\epsilon\bigl(h(f(x_0^{}))\bigr) \) (in gelb).

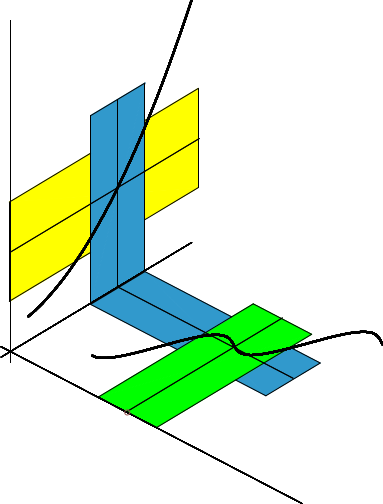
Wenn \( \epsilon \) verkleinert wird, muss man natürlich \( \gamma \) und dann auch \( \delta \) anpassen:

1.12.5. Beispiel.

Wir wollen \( \lim\limits_{x\to0}\dfrac{\sin x}x \) und \( \lim\limits_{x\to0}\dfrac{\tan x}x \) verstehen.

Wegen \( \lim\limits_{x\to0}\sin x=0\pause =\lim\limits_{x\to0}\tan x\pause =\lim\limits_{x\to0}x \) und \( \) haben beide Ausdrücke die Form „\( \frac00 \)” , man kann also die Grenzwertsätze nicht direkt anwenden.

Wir benutzen die Ungleichungen \( 0 \lt x \lt \frac\pi2 \implies \sin x \lt x \pause \lt \tan x \,. \) Anschaulich wird diese Relation an folgender Skizze (hier ist \(x\) die Länge des gestrichelten Bogens):

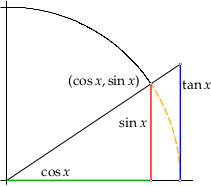
Auch zu diesem Bildchen gibt es eine interaktive Version.

Für \( 0 \lt x \lt \frac\pi2 \) gilt \( \frac{\sin x}x \lt 1 \) und \( 1 \lt \frac{\tan x}x \pause =\frac{\sin x}{x\cdot\cos x} \), also \( \cos x \lt \frac{\sin x}x \).

Damit erhalten wir ein „Sandwich” \( \cos x \lt \frac{\sin x}x \pause \lt 1 \).

Nun gilt \( \lim\limits_{x\to0+0}\cos x=1\pause=\lim\limits_{x\to0+0}1 \), wie im Sandwichsatz 1.5.6 konvergiert also auch der mittlere Term, und wir schließen \( \lim\limits_{x\to0+0}\frac{\sin x}x =1 \).

Als Grenzwert von links erhalten wir \( \lim\limits_{x\to0+0}\frac{\sin (-x)}{-x} = \lim\limits_{x\to0+0}\frac{\sin x}x \), also gilt insgesamt \( \lim\limits_{x\to0}\frac{\sin x}x= 1 \).

Den zweiten gesuchten Grenzwert erhalten wir nun aus \( \lim\limits_{x\to0}\frac{\tan x}x = \pause \lim\limits_{x\to0}\left(\frac{\sin x}x\cdot\frac1{\cos x}\right) \pause =1 \).

1.12.6. Beispiel.

Der Ausdruck \( \lim\limits_{x\to+\infty}\left(\sqrt{x+2}-\sqrt{x-8}\right) \) ist von der Form „\( \infty-\infty \)” . Man findet den Grenzwert durch die folgende Erweiterung: \( \lim\limits_{x\to+\infty}\left(\sqrt{x+2}-\sqrt{x-8}\right) \) \({} = \lim\limits_{x\to+\infty}\dfrac{\left(\sqrt{x+2}-\sqrt{x-8}\right) \color{blue}{\left(\sqrt{x+2}+\sqrt{x-8}\right)}} {\color{blue}{\left(\sqrt{x+2}+\sqrt{x-8}\right)}} \) \({} = \lim\limits_{x\to+\infty}\dfrac{x+2-(x-8)} {\left(\sqrt{x+2}+\sqrt{x-8}\right)} \) \({} = \lim\limits_{x\to+\infty}\dfrac{10} {\left(\sqrt{x+2}+\sqrt{x-8}\right)} \) \({} = 0 \,. \)

Die Erweiterung entspricht dem (aus der Schule bekannten) “Rational-Machen des Nenners” - nur dass wir hier den Zähler rational machen.

1.12.7. Beispiel.

Der Ausdruck \( \lim\limits_{x\to0}\dfrac{1-\cos x}x \) ist von der Form „\( \frac00 \)” .

Durch Erweiterung erhält man: \( \lim\limits_{x\to0}\dfrac{1-\cos x}x \) \({} = \lim\limits_{x\to0}\dfrac{(1-\cos x)\color{blue}{(1+\cos x)}} {x\,\color{blue}{(1+\cos x)}} \) \({} = \lim\limits_{x\to0}\dfrac{1-(\cos x)^2} {x\,\color{blue}{(1+\cos x)}} \) \({} = \lim\limits_{x\to0}\dfrac{\sin x}x \cdot \dfrac{\sin x}{1+\cos x} \) \({} = \lim\limits_{x\to0}\dfrac{\sin x}x \cdot \dfrac{\lim\limits_{x\to0}(\sin x)}{\lim\limits_{x\to0}(1+\cos x)} \) \({} = 1 \cdot \dfrac02 \) \({} = 0 \,. \)

Auch der Ausdruck \( \lim\limits_{x\to0}\dfrac{1-\cos x}{x^2} \) ist von der Form „\( \frac00 \)” .

Durch Erweiterung erhält man hier: \( \lim\limits_{x\to0}\dfrac{1-\cos x}{x^2} \) \({} = \lim\limits_{x\to0}\dfrac{(1-\cos x)\color{blue}{(1+\cos x)}} {{x^2}\,\color{blue}{(1+\cos x)}} \) \({} = \lim\limits_{x\to0}\dfrac{1-(\cos x)^2} {{x^2}\,\color{blue}{(1+\cos x)}} \) \({} = \lim\limits_{x\to0}\left(\dfrac{\sin x}x\right)^2 \cdot \dfrac{1}{1+\cos x} \) \({} = 1^2 \cdot \dfrac12 \) \({} = \dfrac12 \,. \)

1.12.8. Beispiel.

Der Ausdruck \( \lim\limits_{x\to+\infty}\frac{\sin(x^2)}x \) ist von der Form „\( \frac{\text{Gezappel}}\infty \)” .

Man kann ihn mit Hilfe der Sandwich-Abschätzung \( 0\le\left|\sin(x^2)\right|\pause\le1 \) berechnen:

Für \(x \gt 0\) ergibt sich daraus nämlich \( 0\le\left|\frac{\sin(x^2)}x\right| \pause \le\frac1{x} \,. \)

Die linke und die rechte Seite konvergieren mit \( x\to+\infty \) beide gegen \(0\), also auch der Ausdruck in der Mitte: \( \lim\limits_{x\to+\infty}\frac{\sin(x^2)}x = 0 \).