| ↰ 5.1 | Material | 5.4 → |
| ← 5.2 | HM 2 |
Zu den Themen dieses Abschnitts könnte die interaktive Seite zu Vektorfeldern, Kurven(integralen) und Potentialen hilfreich sein.
Es sei \( D\subseteq\RR^n \) offen und \( [a,b] \) ein reelles Intervall.
Eine Abbildung \( C\colon[a,b]\to D\colon{} \) \( t\mapsto C(t) = \left( \begin{array}{c} C_1^{}(t)\\\vdots\\C_n^{}(t) \end{array} \right) \) heißt reguläre Parametrisierung einer Kurve in \(D\), wenn \(C\) stetig differenzierbar ist und für alle \( t\in(a,b) \) gilt:
\( C'(t):= \left( \begin{array}{c} C_1'(t)\\\vdots\\C_n'(t) \end{array} \right) \ne \left( \begin{array}{c} 0\\\vdots\\0 \end{array} \right) \).
Die Kurve, die hier parametrisiert wird, ist
\( K:=\bigset{C(t)}{t\in[a,b]} \) \( \subseteq\RR^n \).
Für jedes stetige Vektorfeld \( g\colon D\to\RR^n \) und jede reguläre Parametrisierung \( C\colon[a,b]\to D \) heißt
\( \alert{\int_a^b g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t} \)
das Kurvenintegral von \(g\) längs \(K\) bezüglich \(C\).
Sind \( C\colon[a,b]\to D \) und \( B\colon[u,v]\to D \) doppelpunktfreie (im Sinne von 5.1.3) und reguläre Parametrisierungen derselben Kurve (d.h. es sei \( \bigset{C(t)}{t\in[a,b]} \) \( = \bigset{B(s)}{s\in[u,v]} \)), so gilt
\( \int_u^v g\bigl(B(s)\bigr)\skalp B'(s) \,\diff s \) \( = \int_a^b g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t \).
In diesem Sinn hängt der Wert des Kurvenintegrals nicht von der Parametrisierung ab.
Man kann daher
\( \alert{\int_K g(x)\skalp\diff x } \) \( := \int_a^b g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t \)
setzen, dabei heißt
\( \diff x \)
vektorielles Bogenelement.
Es handelt sich hier nur um eine Schreibweise: um das Kurvenintegral zu berechnen, muss man eine Parametrisierung \( C\colon[a,b]\to K \) wählen und \( \int_a^b g\bigl(C(t)\bigr)\skalp C'(t)\,\diff t \) berechnen!
Oft kann man nicht die ganze Menge \(K\) auf einmal regulär und doppelpunktfrei (!) parametrisieren. Dann setzt man \(K\) zusammen aus Kurvenstücken \( K_1,\ldots,K_\ell \) so, dass gilt:
Man schreibt in diesem Fall
\( \alert{\int_K g(x)\skalp\diff x} \) \( := \int_{K_1} g(x)\skalp\diff x + \) \( \cdots + \int_{K_\ell} g(x)\skalp\diff x \)
(und muss sich gegebenenfalls den Durchlaufungssinn merken!).
Ist \(g\) ein Kraftfeld, so beschreibt \( \int_K g(x)\skalp\diff x \) die Arbeit, die verrichtet werden muss, um einen Massepunkt längs \(K\) vom Anfangs- zum Endpunkt zu bewegen.
Deswegen nennt man \(\int_K g(x)\skalp\diff x\) auch das Arbeitsintegral.
Gegeben sei das Vektorfeld \( g\colon\RR^2\setminus\left\{\binom00\right\} \to \RR^2 \colon{} \) \( \binom uv \mapsto \frac1{\sqrt{u^2+v^2}} \left( \begin{array}{c} {u\,v} \\ {u^2+2\,v^2} \end{array}\right) \) und die Kurve \(K\) durch die Parametrisierung \( C\colon\left[\frac\pi4,\frac{5\,\pi}4\right] \to \RR^2 \colon{} \) \( t \mapsto C(t):= \binom{\cos t}{\sin t} \).
Die Kurve \(K\) ist also ein Kreisbogen, der Anfangspunkt ist \( C\left(\frac\pi4\right)\pause = \frac12\left({{\sqrt2}\atop{\sqrt2}}\right) \), der Endpunkt \( C\left(\frac{5\,\pi}4\right)\pause = - \frac12\left({{\sqrt2}\atop{\sqrt2}}\right) \).
Mit \( C'(t)= \left({-\sin t \atop\cos t}\right) \) und
\( g\bigl(C(t)\bigr) = \) \( \frac1{\sqrt{(\cos t)^2+(\sin t)^2}} \left({(\cos t)\,(\sin t) \atop (\cos t)^2 + 2\,(\sin t)^2 }\right) \) \( = \left({(\cos t)\,(\sin t) \atop 1 + (\sin t)^2 }\right) \)
ergibt sich \( \int_K g(x)\skalp\diff x \) \( = \ds\int_{\frac\pi4}^{\frac{5\,\pi}4} g\bigl(C(t)\bigr)\skalp C'(t)\,\diff t \) \( = \ds\int_{\frac\pi4}^{\frac{5\,\pi}4} \left({(\cos t)\,(\sin t) \atop 1 + (\sin t)^2 }\right) \skalp\pause\left({-\sin t \atop\cos t}\right)\,\diff t \)
\( = \ds\int_{\frac\pi4}^{\frac{5\,\pi}4} -(\cos t)\,(\sin t)^2 \) \( + \cos t \) \( + (\sin t)^2\,(\cos t) \,\diff t \)
\( = \ds\int_{\frac\pi4}^{\frac{5\,\pi}4} (\cos t) \,\diff t \) \( = \biggl[\,\sin t\,\biggr]_{\frac\pi4}^{\frac{5\,\pi}4} \) \( = -\sqrt2 \).
Es seien \(g\) und \(h\) stetige Vektorfelder. Dann gilt für jede Kurve \(K\) und jede reelle Zahl \(c\):
Weil wir Anfangs- und Endpunkt festlegen, ist auf der Kurve ein Durchlaufungssinn ausgezeichnet.
Um diesen umzukehren, lassen wir den Parameter rückwärts
laufen
:
Die Funktion
\( C^*\colon[a,b]\to\RR^n\colon{} \) \( t\mapsto C(a+b-t) \)
parametrisiert die rückwärts durchlaufene Kurve \(\alert{K^*}\), mit \( s(t):=a+b-t \) gilt \( C^*=C\circ s \), aber auch \( t(s)=a+b-s \).
Wegen \( \frac{\diff}{\diff{t}}C^*(t) \) \( = \frac{\diff}{\diff{t}}C(s(t)) \) \( = C'(s)\cdot{\frac{\diff{s}}{\diff{t}}} \) \( = -C'(s) \) liefert 3.3.1:
\( \ds\int_{K^*}g(x)\skalp\diff x \) \( = \) \( \ds\int_a^b g\bigl(C^*(t)\bigr)\skalp{\tfrac{\diff}{\diff{t}}}\left( C^*(t)\right) \,\diff t \) \( = \) \( \ds\int_{\alert{t=a}}^{\alert{t=b}} g\bigl(C(s(t))\bigr)\skalp C'(s)\,\alert{\tfrac{\diff{s}}{\diff{t}}}\,\diff t \) \( = \) \( \ds\int_{\color{blue}{s=b}}^{\color{blue}{s=a}} g\bigl(C(s)\bigr)\skalp C'(s)\,\diff s \) \( = \color{blue}{-}\ds\int_K g(x)\skalp\diff x \).
Wenn man den Durchlaufungssinn umkehrt, ändert sich also das Vorzeichen des Kurvenintegrals.
Eine Kurve \(K\) mit Parametrisierung \( C\colon[a,b]\to K \) heißt geschlossen (parametrisiert), wenn Anfangs- und Endpunkt zusammenfallen: \( C(a)=C(b) \).
Um anzudeuten, dass über eine geschlossene Kurve integriert wird, schreibt man manchmal auch
\( \alert{\oint_K g(x)\skalp\diff x} \) \( := \int_K g(x)\skalp\diff x \)
und nennt dies ein Umlaufintegral.
Geschlossene Kurven können wir eventuell doppelpunktfrei parametrisieren (also mit einer Parametrisierung \( \) so, dass die Einschränkung \( \) injektiv ist).
In diesem Fall kann man das Umlaufintegral immer noch ohne Zerlegung der Kurve berechnen.
Vorsicht muss man aber beim Umlaufsinn walten lassen!
Es sei \( D=\inn D\subseteq\RR^n \), und es sei \( g\colon D\to\RR^n \) ein stetiges Vektorfeld.
Außerdem sei \( C\colon[a,b]\to D \) eine reguläre Parametrisierung einer Kurve \(K\) in \(D\).
Ist \(g\) ein Gradientenfeld, so hängt das Kurvenintegral nur vom Anfangs- und Endpunkt ab:
Für jedes Potential \(U\) mit \( \grad U=g \) gilt \( \int_K g(x)\skalp\diff x \) \( = \int_a^b g\bigl(C(t)\bigr)\skalp C'(t)\,\diff t \) \( = U\bigl(C(b)\bigr)-U\bigl(C(a)\bigr) \).
Mit anderen Worten: Kurvenintegrale bezüglich Gradientenfeldern sind wegunabhängig.
Nach der Kettenregel 4.8.3 hat die Funktion \( U\circ C\colon[a,b]\to\RR\colon \) \( t\mapsto U\bigl(C(t)\bigr) \) die Ableitung \( \frac{\diff}{\diff t}\bigl(U\circ C\bigr)(t) \) \( = \Jac U{C(t)}\,C'(t) \) \( = \grad U\bigl(C(t)\bigr) \skalp C'(t) \) \( = g\bigl(C(t)\bigr) \skalp C'(t) \). Daraus folgt die Behauptung.
Jetzt ist es aber höchste Zeit, die interaktive Seite zu Vektorfeldern, Kurven(integralen) und Potentialen (wieder) zu besuchen.
Die Formel in 5.3.10 rechtfertigt, jede Potentialfunktion eines Gradientenfelds als Stammfunktion dieses Vektorfelds zu bezeichen.
Außerdem kann man ein Potential zum Gradientenfeld \(g\) ermitteln, indem man eine Stelle \( p\in D \) fest wählt, zu \( q\in D \) jeweils eine Kurve \(K_q\) von \(p\) nach \(q\) durch eine geeignete Funktion \( w_q\colon[a,b]\to D \) parametrisiert und dann
\( (\rfloor)\quad U(q):=\int_{K_q} g(x)\skalp\diff x \) \( = \int_a^b g\bigl(w_q(t)\bigr)\skalp w_q'(t)\,\diff t \)
berechnet.
So erhält man ein Potential \(U\) mit \( U(p)=0 \).
Dass diese Berechnung von \( U(q) \) nicht von der Wahl der Kurve \(K_q\) abhängt, folgt aus 5.3.10.
Als Kurven \(K_q\) wählt man oft Haken
, die jeweils stückweise parallel
zu einer Koordinatenachse verlaufen.
In diesem Fall nennt man die in
\(
(\rfloor)
\)
verwendete Formel für
\(
U(q)
\)
ein Hakenintegral.
Explizite Beispiele solcher Hakenintegrale findet man in 5.3.16 — dort wird das Kurvenintegral manchmal aber auch vom Weg abhängen.
Das Vektorfeld
\( g\colon \RR^3\to\RR^3 \colon{} \) \( \left( \begin{array}{c} x_1^{} \\ x_2^{} \\ x_3^{} \end{array}\right) \mapsto\pause \left( \begin{array}{c} 2\,x_1^{}\,x_2^3\,x_3^{} \\[1ex]\pause 3\,x_1^2\,x_2^2\,x_3^{} \\[1ex]\pause x_1^2\,x_2^3 \end{array}\right) \)
erfüllt \( \Rot g=0 \), und der Definitionsbereich ist einfach zusammenhängend.
Nach 5.2.4 ist \(g\) ein Gradientenfeld.
Eine Potentialfunktion ist
\( U\colon\RR^3\to\RR\colon{} \) \( \left( \begin{smallmatrix} x_1\\x_2\\x_3 \end{smallmatrix} \right) % (x_1^{},x_2^{},x_3^{}) \mapsto x_1^2\,x_2^3\,x_3^{} \).
Für jede stückweise regulär parametrisierte Kurve \(K\) von \( P:= \left(\begin{smallmatrix} 1\\-1\\2 \end{smallmatrix}\right) \) nach \( Q:= \left(\begin{smallmatrix} -3\\2\\5 \end{smallmatrix}\right) \) erhalten wir
\( \int_K g(x)\skalp\diff x \) \( = U(Q)-U(P) \) \( = 9\cdot8\cdot5 - 1\cdot(-1)\cdot2 \) \( = 362 \).
Das Vektorfeld
\( g\colon\RR^2\setminus\left\{\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix}\right)\right\} \to \RR^2 \colon{} \) \( \left( \begin{smallmatrix} u \\ v \end{smallmatrix}\right) \mapsto \frac1{\sqrt{u^2+v^2}} \left( \begin{smallmatrix} {u\,v} \\ {u^2+2\,v^2} \end{smallmatrix}\right) \)
haben wir bereits in 5.3.5 betrachtet. Ein Potential zu \(g\) ist
\( U\colon\RR^2\setminus\left\{\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix}\right)\right\} \to \RR \colon{} \) \( \left( \begin{smallmatrix} u \\ v \end{smallmatrix}\right) \mapsto \pause v\,\sqrt{u^2+v^2} \)
Mit 5.3.10 erhalten wir für jede Kurve \(K\) von \( A:=\frac12\left({{\sqrt2}\atop{\sqrt2}}\right) \) nach \( B:=- \frac12\left({{\sqrt2}\atop{\sqrt2}}\right) \):
\( \int_K g(x)\skalp\diff x \) \( = U(B)-U(A) \) \( = -\frac{\sqrt2}2-\frac{\sqrt2}2 \) \( =-\sqrt2 \).
Besitzt ein Vektorfeld \(g\) eine Potentialfunktion, so wird jedes Umlaufintegral längs einer geschlossenen, stückweise regulär parametrisierten Kurve gleich Null.
Umgekehrt gilt:
Gibt es im Definitionsgebiet des Vektorfelds eine geschlossene, stückweise regulär parametrisierte Kurve \(K\) mit \( \oint_K g(x)\skalp\diff x \ne 0 \), so kann kein Potential für \(g\) existieren.
Wir betrachten das Vektorfeld
\( g\colon\RR^2\setminus\left\{\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix}\right)\right\} \to \RR^2 \colon{} \) \( \left( \begin{smallmatrix} u \\ v \end{smallmatrix}\right) \mapsto \pause \frac1{{u^2+v^2}} \left( \begin{smallmatrix} {-v} \\[2ex]\pause {u} \end{smallmatrix}\right) \)
Der Definitionsbereich ist nicht einfach zusammenhängend, aber wir können Potentiale auf geeigneten Teilmengen angeben:
Auf \( \bigset{\left({ u\atop v}\right)\in\RR^2}{u\ne0} \) ist etwa \( \left({ u\atop v}\right)\mapsto \arctan\left(\frac vu\right) \) ein Potential,
auf der Menge \( \bigset{\left({ u\atop v}\right)\in\RR^2}{v\ne0} \) können wir \( \left({ u\atop v}\right)\mapsto -\arctan\left(\frac uv\right) \) nehmen.
Für jede geschlossene, stückweise regulär parametrisierte Kurve, die eine der Koordinatenachsen meidet, gilt also
\( \oint_K g(x)\skalp\diff x = 0 \).
Wir können dies sogar noch erweitern:
Wegen
\( \frac{\diff}{\diff v}\left(\frac{-v}{u^2+v^2}\right) \) \( = \frac{v^2-u^2}{(u^2+v^2)^2} \) \( = \frac{\diff}{\diff u}\left(\frac{u}{u^2+v^2}\right) \)
besitzt das Vektorfeld \(g\) auf jedem einfach zusammenhängenden Teilgebiet von \( \RR^2\setminus\left\{\left({0\atop0}\right)\right\} \) ein Potential, vgl. 5.2.4.
Solche einfach zusammenhängenden Gebiete können recht kurios aussehen:
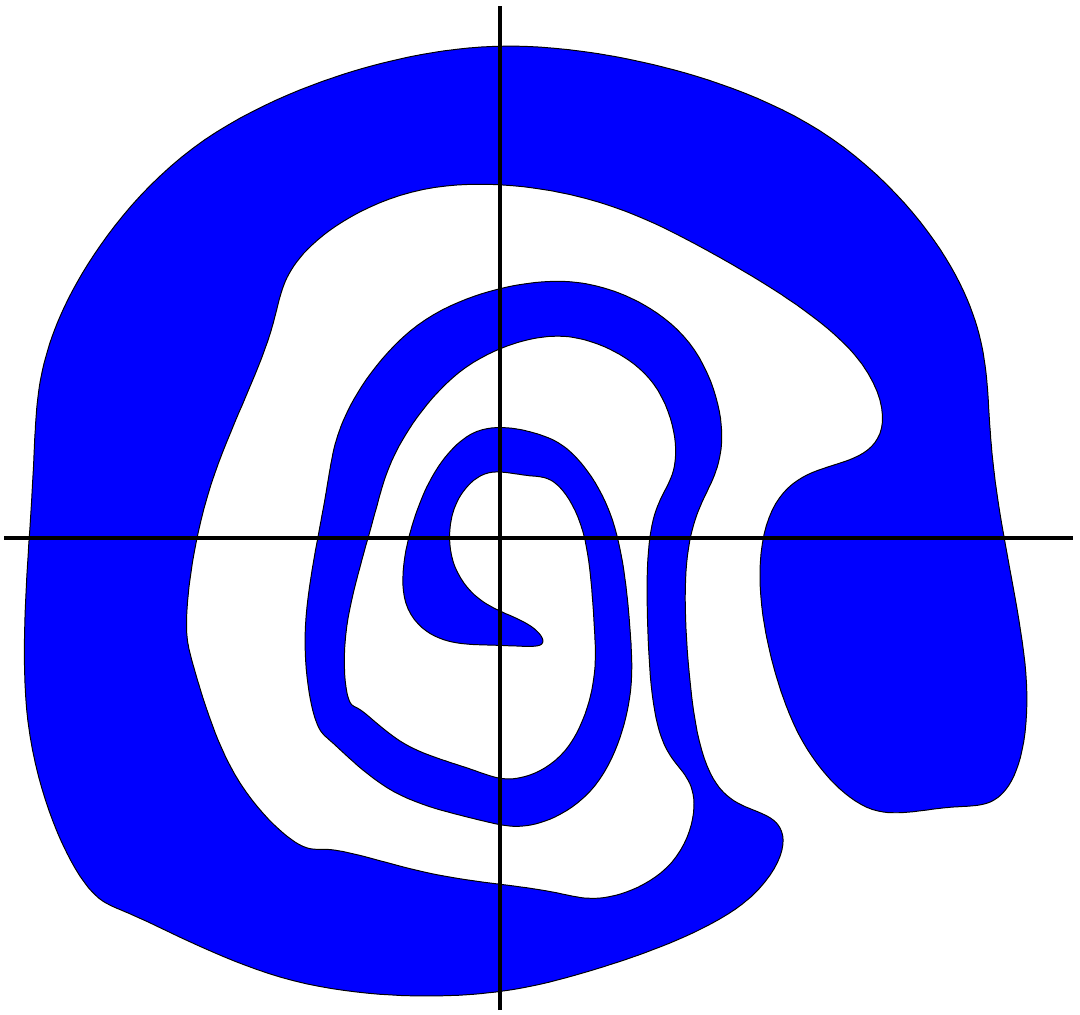
Wir parametrisieren den Einheitskreis \(K_1\):
\( C\colon[0,2\,\pi]\to\RR^2\colon{} \) \( t \mapsto \left( \begin{array}{c} \cos t\\\sin t \end{array}\right) \).
Es gilt
\( g\bigl(C(t)\bigr)\skalp C'(t) \) \( = \) \( \frac1{(\cos t)^2+(\sin t)^2} \binom{-\sin t}{\cos t} \skalp \binom{ -\sin t}{\cos t} \) \( = (-\sin t)^2 + (\cos t)^2 \) \( = 1 \)
und damit
\( \oint_{K_1} g(x) \skalp\diff x \) \( = \int_0^{2\,\pi} g\bigl(C(t)\bigr)\skalp C'(t) \,\diff t \) \( = \int_0^{2\,\pi} 1 \,\diff t \) \( = 2\,\pi \).
Dieses Umlaufintegral wird also nicht Null, und auf keinem Gebiet, das den Einheitskreis enthält, gibt es ein Potential für \(g\):
Insbesondere nicht auf \( \RR^2\setminus\left\{\left({0\atop0}\right)\right\} \).
Wir wollen den Verlauf der Potentialfunktion
\( U\colon \bigset{\left({ u\atop v}\right)\in\RR^2}{u\ne0} \to\RR\colon \) \( \left({ u\atop v}\right) \mapsto \arctan\left(\frac{v}{u}\right) \)
verdeutlichen.
Zur jetzt folgenden Diskussion gibt es auch
ein 3D-Modell, das sie
auch online
bewegen
und erforschen können.
Statt des vollen (unbeschränkten) Definitionsbereichs zeichnen wir in den folgenden Bildern nur den Teil, der im Innern eines Kreises um den Ursprung liegt.
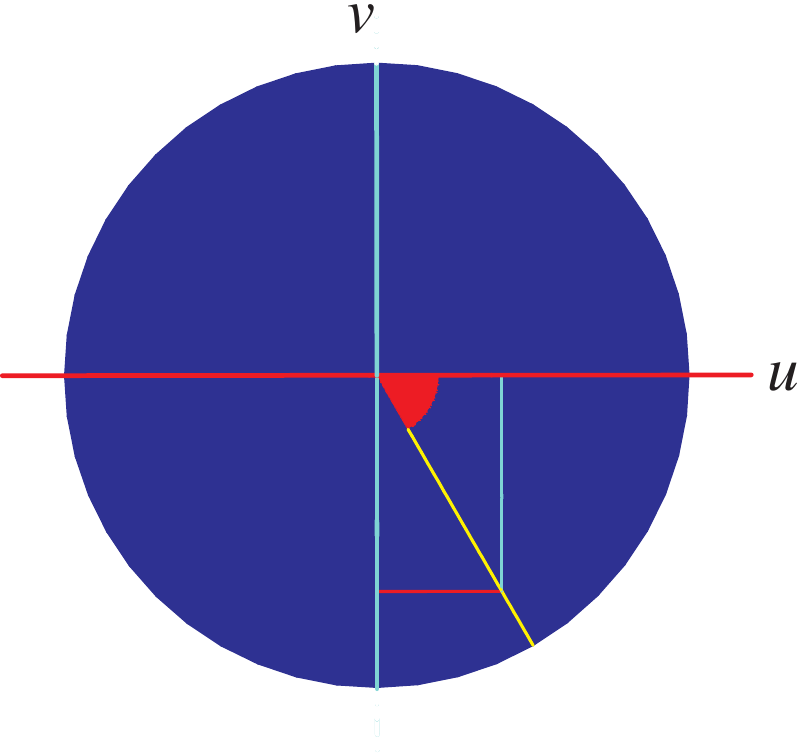
Es gilt \( \frac{v}{u} = \frac{\sin\varphi}{\cos\varphi} {} = \tan\varphi \) für den rot markierten Winkel \( {\color{red}\varphi} \).
Wir erhalten \( U(u,v)=\varphi \) für alle \( \left({ u\atop v}\right)\in \RR^2 \) mit \(u \gt 0\).
Das geht gut, weil wir (in 2.3.4) die Umkehrfunktion \(\arctan\) zu \(\tan\) geeignet gewählt haben.
In diesem Bereich läuft dann \( \alert{\varphi} \) von \( -\frac12\pi \) bis \( \frac12\pi \).
Wenn wir den Winkel \( \varphi \) über \( \frac12\pi \) hinaus bis \( \frac32\pi \) laufen lassen, durchlaufen wir die linke Hälfte des Definitionsgebietes.
Dabei wiederholen sich die Werte für \( \frac{v}{u} \) \( = \frac{-v}{-u} \) \( = \tan\varphi \) \( = \tan(\varphi+\pi) \)
Die durch \( \) gegebene Potentialfunktion \(U\) ist also auf jeder Geraden durch den Ursprung konstant:
Die Schnitte dieser Geraden mit dem Definitionsbereich sind Niveaulinien von \(U\) (Äquipotentiallinien).
Beim Übergang über die Definitionslücke
(\(u = 0 \))
des Potentials springt
der Wert des Potetntials zwischen
\(
-\frac12\pi
\)
und
\(
\frac12\pi
\)
[weil \(\tan\) die Periode
\(
\pi
\)
hat].
Wir verschieben die Andeutung des Definitionsbereichs um \( \frac12\pi \) nach unten (aus dem Weg), und bauen dann den Graphen des Potentials auf — die beiden Sprünge werden klar erkennbar:
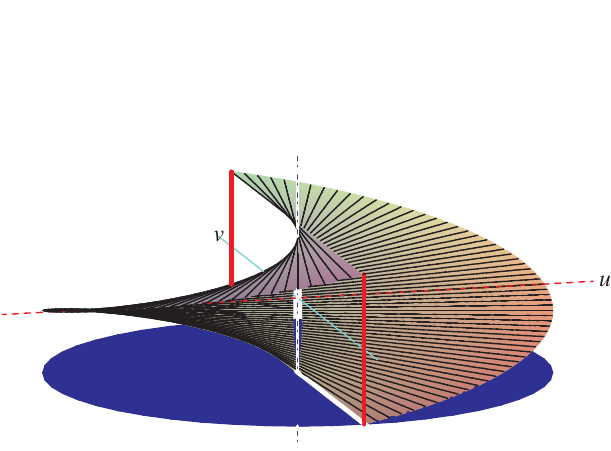
Wenn wir auf der linken Hälfte unser Potential um \( \pi \) nach oben verschieben, schließt sich dieser Teil auf der positiven Hälfte der \(v\)-Achse gut an die rechte Hälfte an.
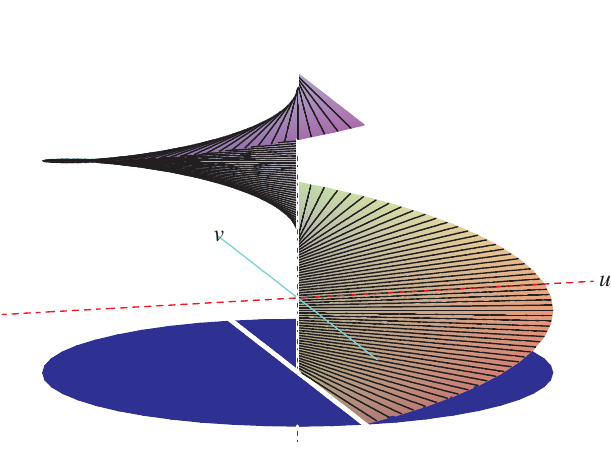
Explizit setzen wir
\( \tilde{U}\binom uv := \) \( \left\{ \begin{array}{rl} \arctan(\frac{v}{u}) & \text{, falls $u>0$,} \\[2ex] \frac12\pi & \begin{array}[t]{r}\text{, falls $u=0$}\\ \text{ und $v>0$,}\end{array} \\[2ex] \pi+\arctan(\frac{v}{u}) & \text{, falls $u<0$.} \end{array} \right. \)
Damit erhalten wir eine Potentialfunktion \( \tilde{U}\colon \RR^2\setminus\bigset{\textstyle\left({ 0\atop v}\right)}{v\le0}\to\RR \).
Diese Funktion \( \) ist stetig (sogar differenzierbar), es gibt aber keine stetige Fortsetzung auf einen größeren Teil der Ebene.
Wir verschieben die Andeutung des Definitionsbereichs wieder um \( \frac12\pi \) nach unten (aus dem Weg), und bauen dann den Graphen des neuen Potentials \( \tilde{U} \) auf — am Ende bleibt immer noch ein Sprung.
(Durch Klick auf das Bild starten Sie eine Video-Animation.)
Außer dem eben betrachteten Vektorfeld
\( g\colon\RR^2\setminus\left\{\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix}\right)\right\} \to \RR^2 \colon{} \) \( \left( \begin{smallmatrix} u \\ v \end{smallmatrix}\right) \mapsto \pause \frac1{{u^2+v^2}}\left( \begin{smallmatrix} -v \\ u \end{smallmatrix}\right) \)
betrachten wir das Vektorfeld
\( f\colon\RR^2\to\RR^2\colon {} \) \( \left( \begin{smallmatrix} u \\ v \end{smallmatrix}\right) \mapsto \pause \left( \begin{smallmatrix} -v \\ u \end{smallmatrix}\right) \).
Diese beiden Felder wollen wir entlang der folgenden Kurven integrieren:
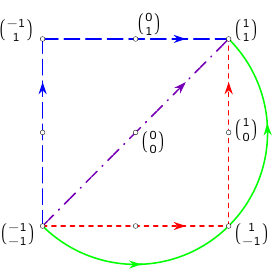
Hier stehen gleich schon Parametrisierungen für diese Kurven:
\( \color{red}{R_1}\colon {} [0,1] \to \RR^2\colon {} \) \( t \mapsto \left( \begin{smallmatrix} -1 \\ -1 \end{smallmatrix}\right) + t \left( \begin{smallmatrix} 2 \\ 0 \end{smallmatrix}\right) = \left( \begin{smallmatrix} 2\,t-1 \\ -1 \end{smallmatrix}\right) \)
\( \color{red}{R_2}\colon {} [0,1] \to \RR^2\colon {} \) \( t \mapsto \left( \begin{smallmatrix} 1 \\ -1 \end{smallmatrix}\right) + t \left( \begin{smallmatrix} 0 \\ 2 \end{smallmatrix}\right) \pause = \left( \begin{smallmatrix} 1 \\ 2\,t-1 \end{smallmatrix}\right) \)
\( \color{blue}{L_1}\colon {} [0,1] \to \RR^2\colon {} \) \( t \mapsto \left( \begin{smallmatrix} -1 \\ -1 \end{smallmatrix}\right) + t \left( \begin{smallmatrix} 0 \\ 2 \end{smallmatrix}\right) \pause = \left( \begin{smallmatrix} -1 \\ 2\,t-1 \end{smallmatrix}\right) \)
\( \color{blue}{L_2}\colon {} [0,1] \to \RR^2\colon {} \) \( t \mapsto \left( \begin{smallmatrix} -1 \\ 1 \end{smallmatrix}\right) + t \left( \begin{smallmatrix} 2 \\ 0 \end{smallmatrix}\right) \pause = \left( \begin{smallmatrix} 2\,t-1 \\ 1 \end{smallmatrix}\right) \)
\( \color{green}{K}\colon {} \left[-\frac34\pi,\frac14\pi\right] \to \RR^2\colon {} \) \( t \mapsto \sqrt2 \, \left( \begin{smallmatrix} \cos(t) \\ \sin(t) \end{smallmatrix}\right) \)
\( \color{darkviolet}{M}\colon {} [-1,1] \to \RR^2\colon {} \) \( t \mapsto t \left( \begin{smallmatrix} 1 \\ 1 \end{smallmatrix}\right) \)
Dabei können wir das Feld \(g\)
wegen der Definitionslücke im Ursprung nicht ohne Weiteres über den
von \(M\) parametrisierten Weg integrieren:
Hier wären uneigentliche Integrale zu betrachten. Da diese hier
nicht konvergieren, lassen wir die Finger davon.
Für den roten Weg rechts um die Ecke
von
\(
\binom{-1}{-1}
\)
nach
\(
\binom11
\)
rechnen wir:
\( \ds\int\limits_R g(x)\skalp\diff x \) \( = \ds\int\limits_{R_1([0,1])}g(x)\skalp\diff x \) \( + \int\limits_{R_2([0,1])}g(x)\skalp\diff x \)
\( = \ds\int_0^1 g(R_1(t))\skalp R_1'(t) \,\diff t \) \( + \ds\int_0^1 g(R_2(t))\skalp R_2'(t) \,\diff t \)
\( = \ds\int_0^1 \frac {\left( \begin{smallmatrix} 1 \\ 2\,t-1 \end{smallmatrix}\right) \skalp \left( \begin{smallmatrix} 2 \\ 0 \end{smallmatrix}\right)}{(2\,t-1)^2+(-1)^2}\, \diff t \) \( + \ds\int_0^1 \frac {\left( \begin{smallmatrix} -(2\,t-1) \\ 1 \end{smallmatrix}\right) \skalp \left( \begin{smallmatrix} 0 \\ 2 \end{smallmatrix}\right)}{1+(2\,t-1)^2} \,\diff t \)
\( = \ds\int_0^1 \frac{2+2}{4\,t^2-4\,t+2}\,\diff t \) \( = \ds\int_0^1 \frac{1}{t^2-t+\frac12}\,\diff t \)
Solche Integrale haben wir in 3.4.9 berechnet:
Mit \( \beta=-1 \) und \( \gamma=\frac12 \) erhalten wir \( \Delta = \gamma-\frac{\beta^2}4 = \frac14 \) und damit
\( \ds \int_R g(x)\skalp\diff x \) \( = \ds\left[\frac{1}{\sqrt\Delta} \arctan\left(\frac{t+\frac\beta2}{\sqrt\Delta}\right)\right]_0^1 \) \( = \ds\left[\strut 2\,\arctan\left(2\,t-1\right)\right]_0^1 \) \( = 2\,\left(\arctan(1)-\arctan(-1)\right) \) \( = \pi \).
Für den blauen Weg links um die Ecke
von
\(
\binom{-1}{-1}
\)
nach
\(
\binom{1}{1}
\)
erhalten wir ganz analog
\( \ds\int_L g(x)\skalp\diff x \) \( = \ds\int\limits_{L_1([0,1])}g(x)\skalp\diff x \) \( + \int\limits_{L_2([0,1])}g(x)\skalp\diff x \) \( = \ds\int_0^1 \frac{-2-2}{4\,t^2-4\,t+2}\,\diff t \) \( = \ds\int_0^1 \frac{-1}{t^2-t+\frac12}\,\diff t \) \( = -\pi \).
Die beiden bis jetzt berechneten Integrale nennt man (wegen der Form der Kurven \(R\) bzw. \(L\)) Hakenintegrale.
Offenbar hängt der Wert des Kurvenintegrals davon ab, auf welcher
Seite
man um die Definitionslücke herum geht.
Da das Vektorfeld \(g\) wirbelfrei ist, hängt der Wert des Integrals nicht vom Weg ab, so lange wir auf derselben Seite bleiben:
Die Integrationswege liegen dann beide innerhalb eines einfach zusammenhängenden Teilgebiets des Definitionsbereichs.
In der Tat ergibt sich beispielsweise bei Integration längs
\(K([-\frac{3}4\pi,\frac14\pi])\)
(also rechts herum
):
\( \ds\int\limits_{K{\scriptstyle([-\frac{3}4\pi,\frac14\pi])}} g(x)\skalp\diff x \) \( = \ds\int\limits_{-\frac{3\,\pi}4\ }^{\frac\pi4} g\left(K(t)\right) \skalp K'(t) \,\diff t \) \( = \ds\int\limits_{-\frac{3\,\pi}4\ }^{\frac\pi4} \frac{2\,\left( \begin{smallmatrix} -\sin(t) \\ \cos(t) \end{smallmatrix}\right)\skalp \left( \begin{smallmatrix} -\sin(t) \\ \cos(t) \end{smallmatrix}\right)}{2(\cos(t)^2+\sin(t)^2)} \,\diff t \) \( = \ds\int\limits_{-\frac{3\,\pi}4\ }^{\frac\pi4} 1 \,\diff t \) \( = \pi \).
Das Vektorfeld \(f\) ist nicht wirbelfrei: Es gilt
\( \Rot f\binom uv \) \( = \frac{\diff f_2}{\diff u}\binom uv - \frac{\diff f_1}{\diff v}\binom uv \) \( = 1-(-1) \) \( = 2 \).
Deswegen können Kurvenintegrale dieses Feldes auch im einfach zusammenhängenden Definitionsgebiet vom gewählten Weg abhängen.
In der Tat gilt
\( \ds\int_R f(x)\skalp\diff x \)
\( = \) \( \ds\int_0^1 \left( \begin{array}{c} 1 \\ 2\,t-1 \end{array}\right) \skalp\left( \begin{array}{c} 2 \\ 0 \end{array}\right) \,\diff t \) \( + \ds \int_0^1 \left( \begin{array}{c} -2\,t+1 \\ 1 \end{array}\right) \skalp\left( \begin{array}{c} 0 \\ 2 \end{array}\right) \,\diff t \)
\( = \ds\int_0^1 (2+2) \,\diff t \) \( = 4 \).
\( \ds\int_L f(x)\skalp\diff x \)
\( = \) \( \ds\int_0^1 \left( \begin{array}{c} -2\,t+1 \\ -1 \end{array}\right) \skalp\left( \begin{array}{c} 0 \\ 2 \end{array}\right) \,\diff t \) \( + \ds \int_0^1 \left( \begin{array}{c} -1 \\ 2\,t-1 \end{array}\right) \skalp\left( \begin{array}{c} 2 \\ 0 \end{array}\right) \,\diff t \)
\( = \ds\int_0^1 (-2-2) \,\diff t \) \( = -4 \).
\( \, \ds\int\limits_{K{\scriptstyle([-\frac{3}4\pi,\frac14\pi])}} f(x)\skalp\diff x \)
\( = \) \( \ds\int\limits_{-\frac{3\,\pi}4\ }^{\frac\pi4} \kern-.3em \sqrt2 \left( \begin{array}{c} -\sin(t) \\ \cos(t) \end{array}\right) \skalp \sqrt2 \left( \begin{array}{c} -\sin(t) \\ \cos(t) \end{array}\right) \,\diff t \) \( = 2\,\pi \).
\( \ds\int\limits_{M{\scriptstyle([-1,1])}} f(x)\skalp\diff x \) \( = \ds\int_{-1}^{1} \left( \begin{array}{c} -t \\ t \end{array}\right) \skalp\left( \begin{array}{c} 1 \\ 1 \end{array}\right) \,\diff t \) \( = 0 \).
Wir wollen Kurvenintegrale benutzen, um Potentialfunktionen zu bestimmen. Dabei setzen wir die Existenz eines Potentials voraus (diese wird durch abstrakte Kriterien wie 5.1.5 gesichert).
Wir wollen das Potential berechnen, indem wir über geeignete Kurven integrieren. Dabei benutzen wir notfalls Kurven, die nur stückweise regulär sind.
Es sei \( g\colon D\to\RR^n \) ein Gradientenfeld auf einem Gebiet \( D\subseteq\RR^n \).
Wir legen einen Punkt \( q_0^{}\in D \) als Startpunkt fest.
Für jeden Punkt \( q\in D \) sei eine (stückweise regulär parametrisierte) Kurve \( K_q \) ausgewählt, die in \(D\) von \(q_0\) nach \(q\) verläuft.
Dann wird durch \( U\colon D\to\RR\colon {} \) \( q\mapsto \int\limits_{K_q} g(x) \skalp\diff x \) ein Potential für \(g\) definiert.
Da das Integral \( \int\limits_{K_q} g(x) \skalp\diff x \) nicht vom gewählten Weg \(K_q\), sondern nur vom Anfangspunkt \(q_0\) und dem Endpunkt \(q\) abhängt, hängt unsere Definition von \(U\) nur von der Wahl des Startpunkts \(q_0\), aber nicht wirklich von den explizit benutzten Wegen ab.
Es sei \( P\colon D\to\RR \) irgendein Potential zu \(g\).
Dies existiert, weil wir \(g\) als Gradientenfeld vorausgesetzt haben.
Dann gilt für jeden Punkt \( q\in D \) und jede stückweise regulär parametrisierte Kurve \( K_q \), die in \(D\) von \( q_0^{} \) nach \( q \) verläuft:
\( P(q)-P(q_0^{}) \) \( = \int\limits_{K_q} g(x)\skalp\diff x \) \( = U(q) \).
Also unterscheidet sich die Funktion \(U\) von dem Potential \(P\) nur um eine additive Konstante, und ist damit selbst ein Potential.
Wir betrachten das Feld
\( g\colon \RR^2 \to\RR^2\colon \) \( \left( \begin{array}{c} u \\ v \end{array}\right) \mapsto\left( \begin{array}{c} v \\ u+v^2 \end{array}\right) \).
Die Jacobi-Matrix \( \Jaco g \binom uv \) \( = \left( \begin{array}{cc} 0 & 1 \\ 1 & 2\,v \end{array}\right) \) ist symmetrisch.
Da das Feld \(g\) demnach wirbelfrei und der Definitionsbereich \(\RR^2\) einfach zusammenhängend ist, ist \(g\) ein Gradientenfeld.
Wir wählen als Startpunkt \( q_0 := \binom10 \) und betrachten für \( q= \binom ab \) die Wege
\( H_a\colon[0,1]\to\RR^2\colon \) \( t \mapsto \left( \begin{array}{c} 1+t\,(a-1) \\ 0 \end{array}\right) \)
\( V_{(a,b)}\colon[0,1]\to\RR^2\colon \) \( t \mapsto \left( \begin{array}{c} a \\ t\,b \end{array}\right) \)
\( D_{(a,b)}\colon[0,1]\to\RR^2\colon \) \( t \mapsto q_0^{}+t\,(q-q_0^{}) \) \( = \left( \begin{array}{c} 1+t\,(a-1) \\ t\,b \end{array}\right) \).
Die von den Wegen \( H_{a} \) bzw. \( V_{(a,b)} \) parametrisierten Kurven \( K_a \) bzw. \( K_a^b \) verbinden \( q_0 =\binom 10 \) mit \( \binom a0 \) bzw. \( \binom a0 \) mit \( \binom ab = q \).
Damit erhalten wir eine stückweise regulär parametrisierte Kurve \( K_q \), die \(q_0\) mit \(q\) verbindet, indem wir \(K_a\) und \(K_a^b\) aneinandersetzen.
Der Weg \( D_{(a,b)} \) parametrisiert eine Kurve \(L_q\) , die \(q_0\) direkt mit \(q\) verbindet.
Das gesuchte Potential erhalten wir jetzt z.B. als Hakenintegral:
\( U(q) := \) \( \ds\int_{K_q} g(x)\skalp\diff x \)
\( = \ds\int\limits_{K_a^{}} g(x)\skalp\diff x \) \( + \ds\int\limits_{K_a^b} g(x)\skalp\diff x \)
\( = \) \( \ds\int_0^1 g\left(H_a^{}(t)\right)\skalp (H_a^{})'(t)\,\diff t \) \( + \) \( \ds\int_0^1 g\left(V_{(a,b)}(t)\right)\skalp (V_{(a,b)})'(t)\,\diff t \).
Die beiden Teilintegrale berechnen wir als
\( \ds\int_0^1 g\left(H_a^{}(t)\right)\skalp (H_a^{})'(t)\,\diff t \) \( = \ds\int_0^1 \left( \begin{array}{c} 0 \\ 1+t\,(a-1) \end{array}\right)\skalp \left( \begin{array}{c} a-1 \\ 0 \end{array}\right) \,\diff t \) \( = \ds\int_0^1 0\,\diff t \) \( = 0 \)
sowie
\( \ds\int_0^1 g\left(V_{(a,b)}(t)\right)\skalp (V_{(a,b)})'(t)\,\diff t \) \( = \ds\int_0^1 \left( \begin{array}{c} t\,b \\ a+t^2\,b^2 \end{array}\right)\skalp \left( \begin{array}{c} 0 \\ b \end{array}\right) \,\diff t \) \( = \ds\int_0^1 a\,b + t^2\,b^3 \,\diff t \) \( = \ds\left[t\,a\,b + t^3\,\frac{b^3}3 \right]_0^1 \) \( = \ds a\,b + \frac{b^3}3 \).
Wir erhalten also
\( U(q) = U\binom ab \) \( = a\,b + \frac{b^3}3 \).
Wenn wir den direkten Weg \( D_{(a,b)} \) benutzen, rechnen wir
\( \ds\int_0^1 g(D_{(a,b)}(t))\skalp (D_{(a,b)})'(t)\,\diff t \) \( = \) \( \ds\int_0^1 \!\left( \begin{array}{c} t\,b \\ \! 1+t\,(a-1)+t^2\,b^2 \! \end{array}\right) \!\skalp\! \left( \begin{array}{c} \! a-1 \! \\ b \end{array}\right) \diff t \) \( = \ds\int_0^1 \! tb(a-1) + b + t(a-1)b + t^2b^3 \,\diff t \) \( = \ds\left[t^2\,b\,(a-1) + b\,t + t^3\,\frac{b^3}3 \right]_0^1 \) \( = \ds a\,b + \frac{b^3}3 \).
und erhalten dasselbe Potential (wie erwartet).
| ↰ 5.1 | Material | 5.4 → |
| ← 5.2 | HM 2 |