| ↰ 1.1 | Material | 1.5 → |
| ← 1.3 | HM 2 | 2.1 ↳ |
Eine Folge \((a_n)_{n\in\NN}\) reeller Zahlen heißt konvergent gegen den Grenzwert \(a\), wenn es zu jedem \(\epsilon\gt0\) eine natürliche Zahl \(n_\epsilon\) so gibt, dass für alle natürlichen Zahlen \(n\) mit \(n \gt n_\epsilon\) gilt:
\( |a-a_n| \lt \epsilon \,. \)
Man nennt den Grenzwert auch Limes der Folge, und schreibt
\( \alert{a=\lim\limits_{n\to\infty}a_n} \,. \)
Man sagt dann auch: Die Folge \((a_n)_{n\in\NN}\) konvergiert gegen \(a\).
Wenn es kein reelles \(a\) gibt, gegen das die Folge konvergiert, nennt man die Folge divergent.
In Quantoren ausgedrückt, lautet die Bedingung für Konvergenz gegen \(a\):
\( \forall\,\epsilon \gt 0 \quad \exists\,n_\epsilon\in\NN \quad \forall\,n \gt n_\epsilon\colon{}\quad |a-a_n| \lt \epsilon \,. \)
Wenn eine Folge nicht konvergiert, so wird sie doch wenigstens Häufungspunkte haben.
Man bezeichnet mit \(\ds\limsup\limits_{n\to\infty}a_n\) (Limes superior) den größten Häufungspunkt der Folge \((a_n)_{n\in\NN}\).
Mit \(\liminf\limits_{n\to\infty}a_n\) (Limes inferior) wird der kleinste Häufungspunkt bezeichnet.
In beiden Fällen muss man auch uneigentliche Häufungspunkte (also \(+\infty\) und \(-\infty\)) in Betracht ziehen!
Die Folge \(\left(\frac1n\right)_{n\in\NN}\) konvergiert gegen \(0\).
Nach dem Archimedischen Prinzip 0.2.3 gibt es zu jedem \(\epsilon \gt 0\) eine natürliche Zahl \(n_\epsilon\) mit \(n_\epsilon \gt \frac1\epsilon\).
Für alle \(n \gt n_\epsilon\) gilt nun
\( \frac1n \lt \frac1{n_\epsilon} \lt \frac1{\,\,\frac1\epsilon\,\,} = \epsilon \,. \)
Also gilt für alle \(n \gt n_\epsilon\):
\( \left| 0-\frac1n \right| = \frac1n \lt \epsilon \,. \)
Damit haben wir \(\lim\limits_{n\to\infty}\frac1n = 0\) bewiesen.
Es gilt \(\lim\limits_{n\to\infty} \frac n{n+1} =1 \).
Zu jedem beliebigen \(\epsilon \gt 0\) gibt es \(n_\epsilon\in\NN\) mit \(1+n_\epsilon \gt \frac1\epsilon\).
Für \(n \gt n_\epsilon\) gilt nun \(1+n \gt 1+n_\epsilon\) und damit
\(\renewcommand{\arraycolsep}{0.2em} \begin{array}{rcl} \epsilon \gt \ds\frac1{1+n_\epsilon} & \gt & \ds\frac1{1+n} \\[2ex] & = & \ds\left|\frac{1}{1+n}\right| \\[2ex] & = & \ds\left|\frac{1+n-n}{1+n}\right| = \left|\frac{1+n}{1+n}-\frac n{n+1}\right| = \left|1-\frac{n}{1+n}\right| \,. \end{array} \)
Damit haben wir die Konvergenz nachgewiesen.
Die Folge \(\left(\sqrt{n+1}-\sqrt{n}\right)_{n\in\NN}\) konvergiert gegen \(0\).
Wir erweitern:
\( \begin{array}{rcl} \sqrt{n+1}-\sqrt{n} & = & \ds \frac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}} \\ & = & \ds \frac{n+1-n}{\sqrt{n+1}+\sqrt{n}} \quad = \quad \ds \frac{1}{\sqrt{n+1}+\sqrt{n}} \,. \end{array} \)
Da der Nenner des rechts stehenden Ausdrucks über alle Grenzen wächst, konvergiert die Folge gegen \(0\).
Direkt auf die Definition 1.4.1 zurückgeführt:
Man wählt \(n_\epsilon \gt \dfrac1{\epsilon^2}\), dann gilt
\( \forall n \gt n_\epsilon\colon \left|\left(\sqrt{n+1}-\sqrt{n}\right) - 0 \right| = \dfrac1{\sqrt{n+1}+\sqrt{n}} \lt \dfrac1{\sqrt{n}} \lt \epsilon \,. \)
Indem man etwa die beiden eben betrachteten Folgen mischt
,
kann man divergente Folgen mit unterschiedlichen Häufungspunkten
erzeugen.
Für \(\epsilon \gt 0\) und \(a\in\RR\) definiert man
\( \alert{U_\epsilon(a) := \bigset{x\in\RR}{|x-a| \lt \epsilon}} \,. \)
Man nennt \(U_\epsilon(a)\) die \(\epsilon\)-Umgebung von \(a\).
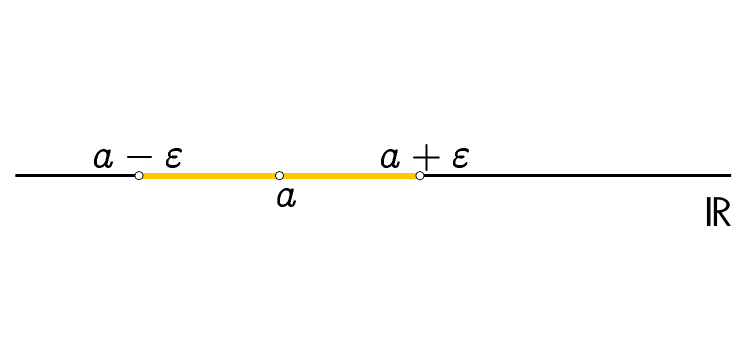
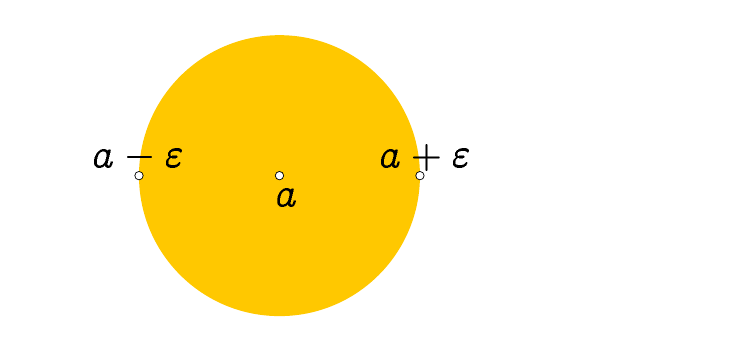
Man kann solche Umgebungen auch in \(\CC\) definieren, dann erhält man das Innere des Kreises vom Radius \(\epsilon\) um \(a\) (vgl. die rechte Skizze).
Eine Folge \((a_n)_{n\in\NN}\) konvergiert genau dann gegen \(a\), wenn in jeder \(\epsilon\)-Umgebung von \(a\) alle Folgenglieder bis auf endlich viele Ausnahmen liegen.
Statt alle bis auf endlich viele Ausnahmen
sagt man auch fast alle
.
Damit haben wir den Gebrauch der Formulierung fast alle
mathematisch präzisiert:
Wenn jedes tausendste Folgenglied nicht in einer gegebenen Umgebung liegt,
liegen im hier definierten Sinn nicht fast alle Glieder in dieser
Umgebung,
denn es liegen ja noch unendlich viele draußen!
Als direkte Umformulierung von 1.4.5 erhalten wir:
Eine reelle Folge ist genau dann divergent, wenn es zu jeder reellen Zahl \(a\) ein \(\epsilon \gt 0\) so gibt, dass unendlich viele Folgenglieder außerhalb von \(U_\epsilon(a)\) liegen.
Die Folge \(\left((-1)^n\right)_{n\in\NN}\) ist divergent.
Zu jedem \(a\in\RR\) gibt es ein \(\epsilon \gt 0\) so, dass unendlich viele Folgenglieder nicht in \(U_\epsilon(a)\) liegen:
Wir können etwa \(\epsilon=\frac12\) nehmen.
Es gibt Folgen, die deswegen divergent sind,
weil sie ziellos in \(\RR\) herumirren
.
Andere scheinen dagegen ein klares Ziel zu haben, das nur leider nicht im Reellen liegt:
Es sei \((a_n)_{n\in\NN}\) eine Folge reeller Zahlen.
Man sagt die Folge strebt gegen \(+\infty\)
,
wenn es zu jeder reellen Zahl \(s\)
eine natürliche Zahl \(n_s\) so gibt,
dass für alle \(n \gt n_s\) gilt: \(a_n \gt s\).
Mit anderen Worten: Fast alle Folgenglieder sind größer als \(s\).
Man schreibt in diesem Fall \(\alert{\lim\limits_{n\to\infty}a_n=+\infty}\).
Es gibt keinen reellen Grenzwert, die Folge ist nicht konvergent!
Analog sagt man die Folge strebt gegen \(-\infty\)
(und schreibt \(\alert{\lim\limits_{n\to\infty}a_n=-\infty}\)),
wenn für jede reelle Zahl \(s\) fast alle Folgenglieder kleiner als \(s\)
sind.
Folgen, die gegen \(+\infty\) oder gegen \(-\infty\) streben, nennt man auch bestimmt divergent (gegen \(+\infty\) bzw. \(-\infty\)).
Es sei \((x_n)_{n\in\NN}\) eine Folge reeller Zahlen.
Die Folge konvergiert genau dann, wenn sie nur einen einzigen Häufungspunkt hat und dieser reell ist.
In diesem Fall gilt \(\limsup\limits_{n\to\infty}x_n=\liminf\limits_{n\to\infty}x_n\), dieser Wert ist reell, und er stimmt mit dem Grenzwert überein.
Die Folge ist genau dann bestimmt divergent, wenn sie nur einen einzigen Häufungspunkt hat und dieser nicht reell ist.
(Dieser Häufungspunkt ist also \(-\infty\) oder \(+\infty\)).
In diesem Fall gilt wieder \(\limsup\limits_{n\to\infty}x_n= \liminf\limits_{n\to\infty}x_n\), aber dieser Wert liegt jetzt in \(\{-\infty,+\infty\}\).
Eine divergente Folge kann durchaus konvergente Teilfolgen haben.
\(b_n=(-1)^nn\) liefert eine divergente Folge \((b_n)_{n\in\NN}\):
Es gilt \(\limsup\limits_{n\to\infty}b_n = +\infty\), \(\liminf\limits_{n\to\infty}b_n = -\infty\), (diese strebt gegen \(+\infty\), keine Teilfolge konvergiert.
\(c_n=1+(-1)^n\) liefert eine divergente Folge \((c_n)_{n\in\NN}\):
Es gilt \(\limsup\limits_{n\to\infty}c_n = 2\), \(\liminf\limits_{n\to\infty}c_n = 0\), konvergente Teilfolgen sind z.B. \(\blau{(c_{2k})_{k\in\NN}}\) und \(\gruen{(c_{2k+1})_{k\in\NN}}\), mit \(\blau{\lim\limits_{k\to\infty}c_{2k}=2}\) und \(\gruen{\lim\limits_{k\to\infty}c_{2k+1}=0}\).
\(d_n=(1-(-1)^n)n\) liefert eine divergente Folge \((d_n)_{n\in\NN}\):
Es gilt \(\limsup\limits_{n\to\infty}d_n = +\infty\), \({\liminf\limits_{n\to\infty}d_n = 0}\); die Teilfolge \(\blau{(d_{2k})_{k\in\NN}}\) konvergiert.
Wenn man endlich viele konvergente Teilfolgen einer Folge \((a_n)_{n\in\NN}\) derart gefunden hat, dass jeder Index \(n\in\NN\) als Index in wenigstens einer dieser Teilfolgen verwendet wird, dann ist die Menge aller Häufungspunkte der Folge genau die Menge der Grenzwerte dieser Teilfolgen.
In der durch \(a_n=\frac1n+\cos(n\frac\pi2)\) gegebenen Folge haben wir die vier Teilfolgen \((a_{4k})_{k\in\NN}\), \((a_{4k-3})_{k\in\NN}\), \((a_{4k-2})_{k\in\NN}\), \((a_{4k-1})_{k\in\NN}\).
Diese konvergieren gegen \(1\), gegen \(0\), gegen \(-1\) und gegen \(0\).
Die Menge aller Häufungspunkte der Folge ist \(\{-1,0,1\}\).
Das Verfahren klappt nicht bei allen Folgen.
Zum Beispiel hat die Folge \((\sin(n))_{n\in\NN}\) unendlich viele Häufungspunkte:
Jeder Punkt im Intervall \([-1,1]\) ist Häufungspunkt (aber das ist schwer zu beweisen).
Das Konvergenzverhalten einer Folge reeller Zahlen ändert sich nicht, wenn man endlich viele Folgenglieder ändert oder ganz entfernt.
Insbesondere gilt:
Es sei \((a_n^{})_{n\in\NN}\) eine Folge reeller Zahlen.
Wir betrachten die Teilfolge \((a_{N+k}^{})_{k\in\NN}\):
\( a_{N+1}^{} \,,\quad % a_{N+2}^{} \,,\quad % a_{N+3}^{} \,,\quad% \ldots % \)
Die Folge \((a_n^{})_{n\in\NN}\) konvergiert genau dann, wenn die Teilfolge (das Endstück) \((a_{N+k}^{})_{k\in\NN}\) konvergiert.
Der Grenzwert ist dann derselbe.
Man schreibt \( \lim\limits_{\alert{n \gt N}}a_n^{} = \lim\limits_{k\to\infty}a_{N+k}^{} \).
| ↰ 1.1 | Material | 1.5 → |
| ← 1.3 | HM 2 | 2.1 ↳ |