| ↰ 1.1 | Material | 1.6 → |
| ← 1.4 | HM 2 | 2.1 ↳ |
Jede konvergente Folge reeller Zahlen besitzt genau einen Grenzwert.
Hätte die Folge zwei Grenzwerte \(a\) und \(b\), so wären fast alle Folgenglieder in \(U_{\frac12|a-b|}(a)\) und auch fast alle Folgenglieder in \(U_{\frac12|a-b|}(b)\). Das ist unmöglich.
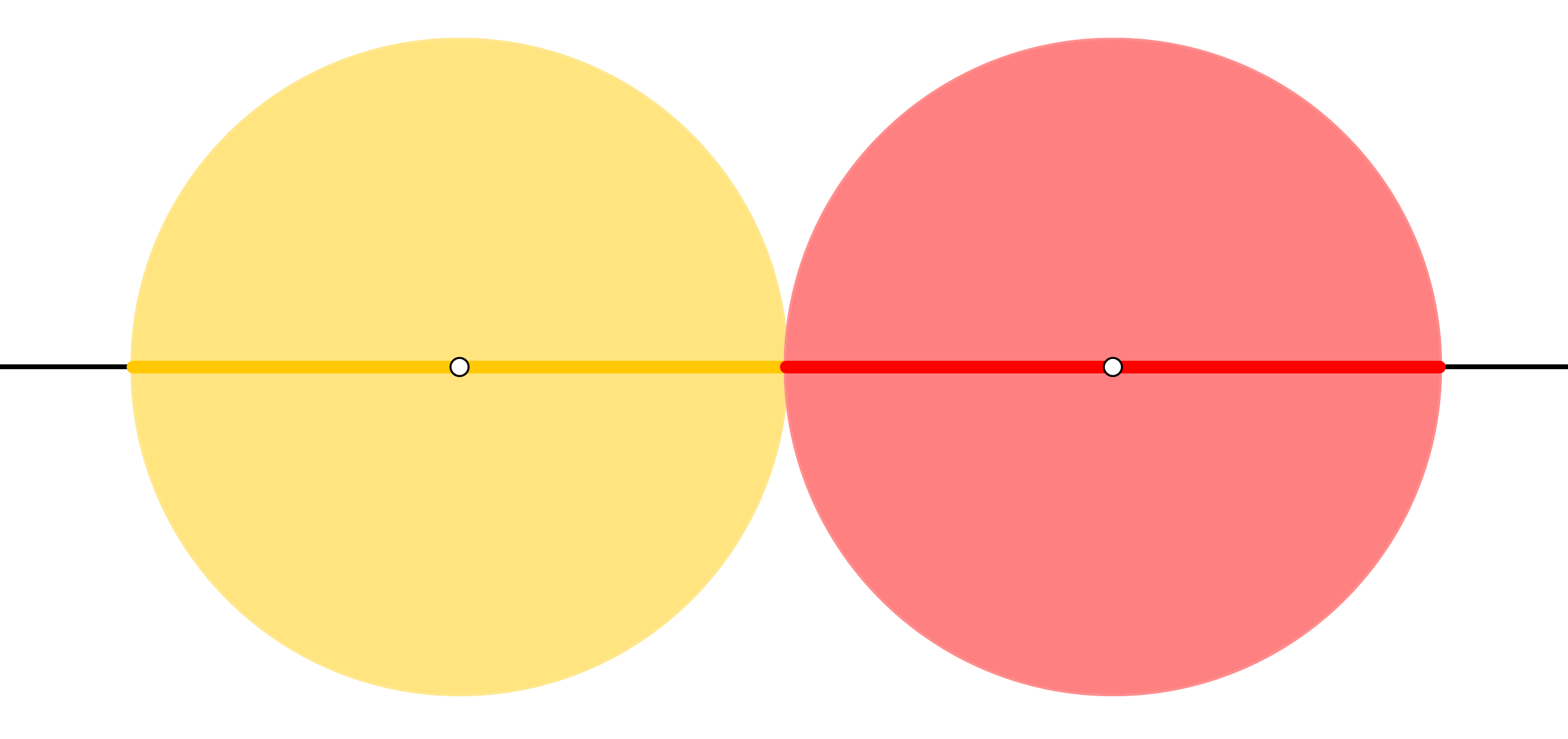
Jede konvergente Folge ist beschränkt.
Es sei \(a\) der Grenzwert der Folge.
Fast alle Folgenglieder liegen in \(U_1(a)\), sind also kleiner als \(a+1\). Die verbleibenden (endlich vielen) können sich von \(a+1\) nicht mehr beliebig weit entfernen. So sieht man, dass die Folge nach oben beschränkt ist.
Analog weist man Beschränktheit nach unten nach.
Es seien \((a_n)_{n\in\NN}\) und \((b_n)_{n\in\NN}\) konvergente Folgen reeller Zahlen:
Es gelte \(\lim\limits_{n\to\infty}a_n=a\) und \(\lim\limits_{n\to\infty}b_n=b\).
Wir überlassen den Beweis den Mathematikern.
Setzt man im Grenzwertsatz für \((b_n)_{n\in\NN}\) eine konstante Folge ein, so erhält man:
Es sei \(k\in\RR\). Konvergiert die reelle Folge \((a_n)_{n\in\NN}\) gegen \(a\), so konvergieren die Folgen
Es seien \((a_n)_{n\in\NN}\) und \((b_n)_{n\in\NN}\) konvergente reelle Folgen.
Gilt für (fast) alle \(n\in\NN\) die Ungleichung \(a_n\le b_n\), so gilt auch \(\lim\limits_{n\to\infty} a_n \le \lim\limits_{n\to\infty} b_n\).
Es seien \((a_n)_{n\in\NN}\), \((b_n)_{n\in\NN}\) und \((c_n)_{n\in\NN}\) reelle Folgen.
Es gebe \(n_0\) so, dass für alle \(n \gt n_0\) gilt:
\( a_n \le b_n \le c_n \,. \)
Konvergieren \((a_n)_{n\in\NN}\) und \((c_n)_{n\in\NN}\) beide gegen den gleichen Grenzwert \(g\), so konvergiert auch \((b_n)_{n\in\NN}\) gegen \(g\).
Für \(c \gt 0\) gilt \(\lim\limits_{n\to\infty}\sqrt[n]c=1\).
Für \(c=1\) ist die Folge konstant (\(\sqrt[n]1=1\)) und daher die Aussage richtig.
Jetzt sei \(c \gt 1\). Man setzt \(a_n:=\sqrt[n]c-1\).
Für alle \(n\in\NN\) gilt dann \(a_n \gt 0\) und \(c=(1+a_n)^n\). Nach dem binomischen Lehrsatz gilt
\( \begin{array}{rcl} c = (1+a_n)^n & = & \ds \binom n0 + \binom n1\,a_n + \binom n2\,a_n^2 + \cdots + \binom nn\,a_n^n \\ & = & 1 + n\,a_n + \underbrace{\binom n2\,a_n^2 + \cdots + \binom nn\,a_n^n}_{ \gt 0} \, \\ \text{also }\qquad c \gt n\,a_n & \gt & 0 \,. \end{array} \)
Daraus folgt \( \dfrac cn % \gt % a_n % \gt % 0 \,. % \)
Wegen \(\lim\limits_{n\to\infty}\frac cn = 0\) und nach dem Sandwichsatz 1.5.6 gilt \( \lim\limits_{n\to\infty}a_n=0 \). Damit ergibt sich
\( \lim\limits_{n\to\infty} \sqrt[n]c = \lim\limits_{n\to\infty} \bigl(\sqrt[n]c - 1\bigr) +1 = \lim\limits_{n\to\infty} a_n +1 = 1 \,. \)
Im Fall \(0 \lt c \lt 1\) gilt \(\frac1c \gt 1\).
Nach dem eben Bewiesenen und den Grenzwertsätzen ergibt sich
\( \lim\limits_{n\to\infty} \sqrt[n]c = \lim\limits_{n\to\infty} \frac1{\sqrt[n]{\frac1c}} = \frac 1{\lim\limits_{n\to\infty} \sqrt[n]{\frac1c}} = 1 \,. \)
Es sei \(q\in\RR\). Wir betrachten die Folge \(\left(q^n\right)_{n\in\NN}\).
Für \(q=-1\) ist die Folge divergent.
Sie häuft sich bei \(1\) und \(-1\), es gilt \(\limsup\limits_{n\to\infty}(-1)^n=1\) und \(\liminf\limits_{n\to\infty}(-1)^n=-1\).
Für \(q \gt 1\) ist die Folge bestimmt divergent:
Es gilt \(\lim\limits_{n\to\infty}q^n=+\infty\).
Für \(q \lt -1\) ist die Folge divergent.
Es gibt bestimmt divergente Teilfolgen, so gilt etwa: \(\lim\limits_{k\to\infty}q^{2k}=+\infty\), \(\lim\limits_{k\to\infty}q^{2k+1}=-\infty\).
Für jede reelle Zahl \(c\) gilt \(\lim\limits_{n\to\infty} \frac{c^n}{n!}=0\).
Zuerst wählen wir \(n_c\in\NN\) so, dass \(|c| \lt n_c\). Nach Division durch \(2\,n_c\) erhalten wir
\( \left|\frac c{2\,n_c}\right| \lt \frac{n_c}{2\,n_c} =\frac12 \,. \)
Für jede natürliche Zahl \(k \gt 2\,n_c\) gilt damit
\(\begin{array}{rcccccl} 0 & \le & \ds\left|\frac{c^k}{k!}\right| & = & \ds\left|\frac{c^{2n_c}}{(2\,n_c)!} \cdot \frac{c}{2\,n_c+1}\cdots\frac{c}{k}\,\right| \\[2ex] &&& \lt & \ds\left|\frac{c^{2n_c}}{(2\,n_c)!} \cdot \quad\,\frac12\quad\cdots\,\frac12\,\right| \\[2ex] &&& = & \ds\left|\frac{c^{2n_c}}{(2\,n_c)!} \cdot \frac1{2^{k-2\,n_c}}\right| & = & \ds\left|\frac{c^{2n_c}}{(2\,n_c)!}\right| \cdot 2^{2\,n_c}\cdot\frac1{2^k} \,. \end{array} \)
Für \(k\to\infty\) konvergiert die rechte Seite gegen \(0\), nach dem Sandwichsatz 1.5.6 erhalten wir
\( \lim\limits_{k\to\infty}\left|\frac{c^k}{k!}\right| = 0 = -0 = \lim\limits_{k\to\infty}-\left|\frac{c^k}{k!}\right| \).
Wegen \(-|x|\le x \le|x|\) liefert eine weitere Anwendung des Sandwichsatzes die Behauptung: \( \lim\limits_{k\to\infty}\frac{c^k}{k!}=0\).
Es gilt \(\lim\limits_{n\to\infty} \sqrt[n]n =1\).
Wir setzen \(a_n:=\sqrt[n]n-1\). Dann gilt
\( n = (1+a_n)^n = 1 + n\,a_n + \binom n2\, a_n^2 + \cdots + a_n^n \gt \binom n2\, a_n^2 = \frac{n(n-1)}2\, a_n^2 \)
und damit für \(n\ge2\):
\( \frac2{n-1} \gt a_n^2 \ge 0 \,. \)
Nach dem Sandwichsatz 1.5.6 folgt \(\lim\limits_{n\ge2}a_n^2=0\).
Wenn man nun weiß, dass die Folge \(\bigl(\sqrt[n]n\bigr)_{n\in\NN}\) konvergiert, dann konvergiert auch die Folge \(\bigl(\sqrt[n]n-1\bigr)_{n\in\NN}\), und für \(a:=\lim\limits_{n\to\infty}\sqrt[n]n-1\) gilt nach den Grenzwertsätzen (vgl. 1.5.3):
\( 0=\lim\limits_{n\to\infty}a_n^2 = \left(\lim\limits_{n\to\infty}\sqrt[n]n-1\right)\, \left(\lim\limits_{n\to\infty}\sqrt[n]n-1\right) = a^2 \,. \)
Dies liefert \(a=0\), und \(\lim\limits_{n\to\infty}\sqrt[n]{n} = \lim\limits_{n\to\infty}(a_n+1) =a+1 =1\), wie behauptet.
Um den eben geführten Beweisgang zu vervollständigen, brauchen wir ein Kriterium für die Konvergenz einer Folge, das noch keine Kenntnis des Grenzwerts verlangt.
Ein solches liefert der Satz von Bolzano und Weierstraß 1.6.5, ein anderes ist nach Cauchy benannt (siehe 1.7.1).
| ↰ 1.1 | Material | 1.6 → |
| ← 1.4 | HM 2 | 2.1 ↳ |